
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства неопределенного интеграла.Содержание книги
Поиск на нашем сайте
1. 3. 4. Отыскание неопределенного интеграла называется интегрированием функции. Таблица основных интегралов:
Интегралы иногда можно найти с помощью непосредственного использования таблицы интегралов и основных свойств неопределенного интеграла. Пример 1. Найти
Методы интегрирования
а) Во многих случаях интегралы можно найти путем введения новой переменной интегрирования. Этот метод называется методом подстановки, или методом замены переменной. Если x=g(t), тогда справедлива следующая формула замены переменной:
Пример 2. Найдем интеграл Необходимо ввести новую переменную t таким образом, чтобы свести данный интеграл к табличному. Обозначим t= 5 x+ 6. Тогда x =(t- 6)/5. – замена. Следовательно, Пример 3. Найдем интеграл: Введем переменную t = 1 - x2. Тогда можно продифференцировать
Следовательно, б) Существует еще один метод интегрирования: интегрирование по частям. Если функции и(х) и v(х) определены и дифференцируемы на некотором множестве D, тогда справедлива формула интегрирования по частям: Пример 4. Найдем интеграл: Обозначим u = x; dv = sinx dx. Для того, чтобы воспользоваться формулой интегрирования по частям, необходимо, найти du и v. Найдем: и = х, значит dи = dx; dv = sinx dx, значит Подставим найденные значения в формулу интегрирования по частям:
Пример 5. Найдём: Обозначим: u=x, dv=e-x dx. Тогда du=dx. Найдем v: v= и, следовательно, Таким образом, v =
Определенный интеграл Геометрический смысл определенного интеграла.
Площадь криволинейной трапеции АВСD, ограниченной линиями х = а, х = b, у = 0 находится как: а и b есть границы интегрирования.
Определенный интеграл находят с помощью формулы Ньютона— Лейбница:
Свойства определенного интеграла. 1. 2. 3. 4.
Замена переменной.
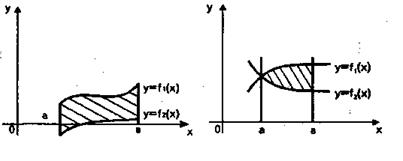
Площади между кривыми.
Рассмотрим фигуру, представляющую собой множество точек, ограниченных линиями: х=а, х=b, у = f1(х), у=f2(x) (a<b, Тогда площади заштрихованной фигуры вычисляется по формуле:
Пример 1.
Пример 2. Вычислим площадь фигуры, ограниченной линиями: у = х2, у2=х. Вначале схематически построим графики указанных линий.
Нам необходимо найти площадь заштрихованной фигуры. Найдём абсциссы точек пересечения указанных линий.
Для этого необходимо решить систему уравнений:
Из последнего уравнения находим абсциссы точек пересечения:
Найдем указанную площадь, воспользовавшись формулой (1)
Пример 3. Вычислить площадь фигуры, ограниченной линиями: у2= 2х + 1, х - у -1= 0. Построим схематически графики указанных линий.
Нам необходимо найти площадь заштрихованной фигуры. Найдем точки пересечения этих линий. Решим систему:
S = SABO + SACD + SBOC = SACD + 2SBOC =
Задания для самостоятельного решения Неопределенный интеграл. 1.1. Найти неопределенный интеграл (интегрирование по свойствам и по таблице интегралов).
1.1.1) 1.1.3) 1.1.5) 1.1.7) 1.11.3) 1.1.15) 1.1.17) 1.1.19) 1.1.21) 1.2. Найти неопределенный интеграл (замена переменной и подстановка)
1.2.1) 1.2.4) 1.2.7) 1.2.10) Указание: в примерах 1.2.10 – 1.2.11 используется формула: 1.2.12) 1.2.15) 1.2.18) 1.2.21)
1.3. Найти неопределенный интеграл (интегрирование по частям).
1.3.1) 1.3.4) 1.3.7) 1.3.10)
1.4. Найти неопределенный интеграл (табличные интегралы вида:
1.4.1) 1.4.4) 1.4.7) 1.4.10) 1.4.13) 1.4.16)
Указание: в примерах 1.4.17, 1.4.18 из подынтегральной неправильной дроби выделить целое выражение.
1.4.19) 1.4.22) 1.4.25)
Указание: в примерах 1.4.19-1.4.25 из квадратичного трехчлена выделить полный квадрат.
Определенный интеграл 2.1. Вычислить определенный интеграл 2.1.1) 2.1.4) 2.1.7) 2.1.10) Геометрические приложения 3.1. Вычислить площадь фигуры, ограниченной линиями.
3.1.1) y=4-x2 , y=0; 3.1.2) y=x2 , y=2x; 3.1.3) y=2x-x2 , y=0; 3.1.4) y=3-2x-x2 , y=0; 3.1.5) y=lnx , x=e, y=0.
3.2. Вычислить объем тела вращения 3.2.1.) Вращаем 3.2.2.) Вращаем
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.196.97 (0.01 с.) |

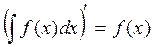 2.
2. 
 , где с = const
, где с = const












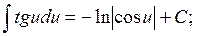

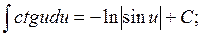



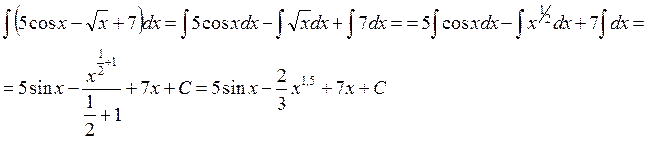

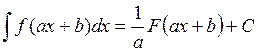 , так как
, так как  .
.
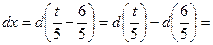
 . Подставим найденные выражения в исходный интеграл:
. Подставим найденные выражения в исходный интеграл: 


 ,
,  .
. . Подставим найденные выражения в интеграл:
. Подставим найденные выражения в интеграл: 

 . Эта формула позволяет свести вычисление
. Эта формула позволяет свести вычисление 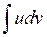 к вычислению
к вычислению  , который иногда может оказаться более простым.
, который иногда может оказаться более простым.



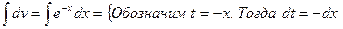

 . Поставим найденные выражения в формулу интегрирования по частям:
. Поставим найденные выражения в формулу интегрирования по частям:
 , где
, где  — определенный интеграл,
— определенный интеграл,
 , где F – первообразная для f(x).
, где F – первообразная для f(x). , где с = const
, где с = const


 ,
,  ,
,  ,
,  .
.
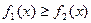 )
) (1)
(1) . Введем новую переменную t=2x. Тогда dt = d2x = 2dx. Следовательно,
. Введем новую переменную t=2x. Тогда dt = d2x = 2dx. Следовательно,  . Найдём пределы интегрирования для переменной t, т.к.
. Найдём пределы интегрирования для переменной t, т.к.  , следовательно,
, следовательно,  . Таким образом:
. Таким образом: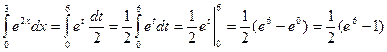







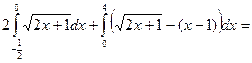

 ; 1.1.2)
; 1.1.2)  ;
; ; 1.1.4)
; 1.1.4)  ;
; ; 1.1.6)
; 1.1.6)  ;
; ; 1.1.8)
; 1.1.8)  ;
; ; 1.14)
; 1.14)  ;
; ; 1.1.16)
; 1.1.16)  ;
; ; 1.1.18)
; 1.1.18)  ;
; ; 1.1.20)
; 1.1.20) 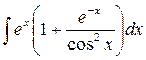 ;
;
 ; 1.2.2)
; 1.2.2)  ; 1.2.3)
; 1.2.3) 
 ; 1.2.5)
; 1.2.5)  ; 1.2.6)
; 1.2.6)  ;
; ; 1.2.8)
; 1.2.8)  ; 1.2.9)
; 1.2.9)  ;
; ; 1.2.11)
; 1.2.11)  ;
; (если числитель дроби есть производная от знаменателя, то интеграл равен логарифму знаменателя).
(если числитель дроби есть производная от знаменателя, то интеграл равен логарифму знаменателя). ; 1.2.13)
; 1.2.13)  ; 1.2.14)
; 1.2.14)  ;
; ; 1.2.16)
; 1.2.16)  ; 1.2.17)
; 1.2.17)  ;
;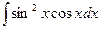 ; 1.2.19)
; 1.2.19)  ; 1.2.20)
; 1.2.20)  ;
; ; 1.2.22)
; 1.2.22)  ;
;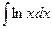 ; 1.3.2)
; 1.3.2)  ; 1.3.3)
; 1.3.3) 
 ; 1.3.5)
; 1.3.5)  ; 1.3.6)
; 1.3.6) 
 ; 1.3.8)
; 1.3.8)  ; 1.3.9)
; 1.3.9) 
 ; 1.3.11)
; 1.3.11) 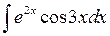 ;
; ;
;  ;
;  и к ним приводящиеся).
и к ним приводящиеся). ; 1.4.2)
; 1.4.2)  ; 1.4.3)
; 1.4.3)  ;
; ; 1.4.5)
; 1.4.5)  ; 1.4.6)
; 1.4.6)  ;
; ; 1.4.8)
; 1.4.8)  ; 1.4.9)
; 1.4.9) 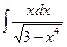 ;
; ; 1.4.11)
; 1.4.11)  ; 4.12)
; 4.12)  ;
; ; 1.4.14)
; 1.4.14)  ; 1.4.15)
; 1.4.15)  ;
;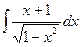 ; 1.4.17)
; 1.4.17)  ; 1.4.18)
; 1.4.18)  ;
; ; 1.4.20)
; 1.4.20)  ; 1.4.21)
; 1.4.21)  ;
; ; 1.4.23)
; 1.4.23) 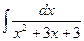 ; 1.4.24)
; 1.4.24)  ;
; ;
; ; 2.1.2)
; 2.1.2)  ; 2.1.3)
; 2.1.3)  ;
; ; 2.1.5)
; 2.1.5)  ; 2.1.6)
; 2.1.6)  ;
;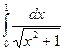 ; 2.1.8)
; 2.1.8) 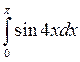 ; 2.1.9)
; 2.1.9)  ;
; .
. на [1; 5] вокруг Oy, Ox.
на [1; 5] вокруг Oy, Ox. на [2; 3] вокруг Ox, Oy.
на [2; 3] вокруг Ox, Oy.


