
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функции нескольких переменных ( ФНП )Содержание книги
Поиск на нашем сайте Частные производные Для ФНП вводится понятие частной производной по соответствующей переменной. В случае функции 2-х переменных:
(записать самостоятельно) Первая формула определяет частную производную по x, а вторая - частную производную по y. Вычисление производных от ФНП выполняется по обычным правилам дифференцирования функций одной переменной, при этом значения всех переменных, кроме одной, по которой вычисляется производная, считаются постоянными.
Задания для самостоятельного решения. 1. Найти все частные производные до второго порядка от функций · · · · · Пример
Дифференциал функции
Дифференциалом функции называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, т.е.:
или
Задания для самостоятельного решения 1. Найти дифференциалы функций 1) 2) ln x·y в точке (x;y)=(10;20) при d x =0,1ln10; d y =0,2ln10. 2. Найти все частные производные
Формула для дифференцирования неявной функции
Неявная функция одной переменной задаётся уравнением
Функция
Задания для самостоятельного решения 1. Используя правило дифференцирования неявно заданной функции найти 1) 2) ln (xy)=0 2. Найти частные производные функции Z, заданной уравнением
Линии уровня Линией уровня функции 2-х переменных Число С в этом случае называется уровнем. Задание для самостоятельного решения. 1. Постройте линии уровня функции
1.5. Применение частных производных в экономике
Пусть спрос- это функция 3-х переменных
Ответ на вопрос, как меняется спрос при изменении цен и доходов, количественно даётся с помощью понятия эластичности. Коэффициенты эластичности. Эластичность спроса от цены (собственной) определяется как
Перекрёстный коэффициент эластичности, определяемый как
Для взаимозаменяемых товаров
Для взаимодополняющих товаров
Эластичность спроса от доходов определяется как
Задания для самостоятельного решения 1. Для функции спроса
2. Для функции спроса при 3. Для функции спроса 4. Для функции 5. Задана функция спроса 6. Известно что функция спроса 1) Коэффициенты эластичности спроса от цены, альтернативной цены и от дохода; 2) Записать выражение для поверхности уровня; 3) Как изменится для поверхности уровня, проходящей через точку М, а) цена товара, если при неизменной альтернативной цене доход потребителя удвоится? б) при неизменном доходе альтернативная цена уменьшится на 30%?
7. Функция спроса Q от цены Р и альтернативной цены 1) записать уравнение линии уровня в точке (Р; 2) определить величину спроса при условии, что цена Р увеличится, а альтернативная цена одновременно уменьшится на 25%.
Полезность
Потреблению благ ставится в соответствие число U, называемое полезностью. Чем выше оценка, которую даёт потребитель этим благам, тем больше число U. Предположим, имеется два вида товара и потребитель покупает первый товар в количестве x 1, а второй – в количестве x 2. Полезность тогда представляет некоторую функцию от x 1 и x 2 U=U(x 1, x 2) Предположим U(3,7)=20; U(4,5)=25, Значит с точки зрения потребителя лучше приобрести 4 единицы первого и пять единиц второго товара. Полезность представляет собой функцию двух переменных (их число может быть больше), для которой могут быть вычислены частные производные:
Эти частные производные получили название предельных полезностей. Если x 1 и x 2 меняются незначительно, то результирующее изменение полезности можно приближенно получить по следующей формуле:
Предельные полезности являются убывающими функциями по соответствующим переменным. То есть, по мере роста количества приобретаемого товара каждая следующая единица товара приносит все меньше удовлетворения потребителю. Этот результат известен как закон убывания предельной полезности.
|
||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 448; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 понятие частной производной определяется следующим образом:
понятие частной производной определяется следующим образом: 
 ......
......



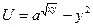



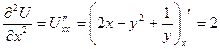





 в точке (x; y)= (1;10) при d x =d y =0,1;
в точке (x; y)= (1;10) при d x =d y =0,1; функции
функции 

 - неявная функция
- неявная функция - формула дифференцирования неявной функции
- формула дифференцирования неявной функции - называется неявной, если она задаётся уравнением
- называется неявной, если она задаётся уравнением
 ;
; 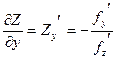
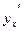 , если
, если
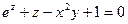
 при U=0;1;4
при U=0;1;4 , где Р- цена, Y- доходы потребителей,
, где Р- цена, Y- доходы потребителей,  - цена альтернативного товара.
- цена альтернативного товара. при неизменных значениях цены альтернативного товара
при неизменных значениях цены альтернативного товара  - формула для точечной эластичности спроса от цены
- формула для точечной эластичности спроса от цены считаются постоянными
считаются постоянными
 - формула перекрестного коэффициента эластичности
- формула перекрестного коэффициента эластичности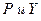 считаются постоянными
считаются постоянными


 - формула для эластичности спроса от доходов
- формула для эластичности спроса от доходов считаются постоянными
считаются постоянными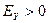 для качественных товаров т.к. спрос на качественные (дорогие) товары увеличивается с ростом доходов.
для качественных товаров т.к. спрос на качественные (дорогие) товары увеличивается с ростом доходов. для низкосортных товаров
для низкосортных товаров (Р- цена,
(Р- цена,  .
. найти эластичность спроса от дохода
найти эластичность спроса от дохода
 эластичность спроса от цены и перекрёстный коэффициент эластичности в точке
эластичность спроса от цены и перекрёстный коэффициент эластичности в точке  .
. найти эластичность спроса от цены при
найти эластичность спроса от цены при 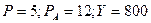
 Как изменится альтернативная цена для фиксированной поверхности уровня при неизменной величине дохода, если цена Р увеличится на 40%?
Как изменится альтернативная цена для фиксированной поверхности уровня при неизменной величине дохода, если цена Р увеличится на 40%? проходит через точку M c координатами (P;
проходит через точку M c координатами (P;  ;
; );
); и
и 




