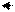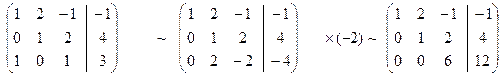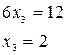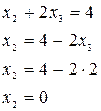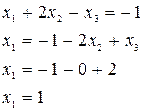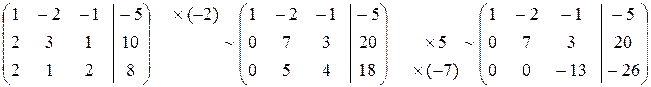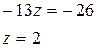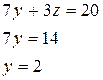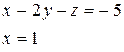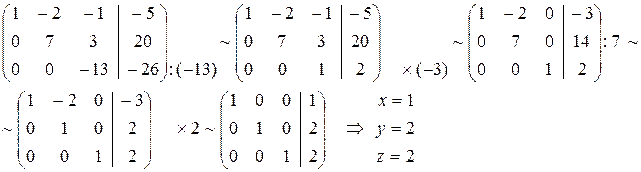Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение систем линейных алгебраических уравнений с квадратной матрицей коэффициентов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Система линейных алгебраических уравнений (СЛАУ) совместна, если имеет хотя бы одно решение и несовместна, если не имеет ни одного решения. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более чем одно решение. Система называется однородной, если все элементы столбца свободных членов b1, b2 … bn равны нулю и неоднородной, если хотя бы один этих элементов отличен от нуля. Для решения СЛАУ с квадратной матрицей коэффициентов разработан ряд методов. Рассмотрим метод определителей (формула Крамера), матричный метод и метод Гаусса: 4.1.1. Метод определителей (формула Крамера) Пусть система
имеет квадратную матрицу коэффициентов, определитель которой не равен нулю. Тогда система имеет единственное решение, которое по формулам Крамера записывается:
где Пример.
Решение.
Проверка
Метод определителей позволяет решать системы только с квадратной матрицей коэффициентов при условии, что 4.1.2. Матричный метод (математический метод, метод обратнойматрицы) Пусть система
Имеет квадратную матрицу коэффициентов, определитель которой не равен нулю. Тогда система имеет единственное решение, которое представляется в следующем виде:
Матричный метод позволяет решать системы только с квадратной матрицей коэффициентов при условии, что
Пример.
Решение.
4.1.3. Метод Гаусса (универсальный метод) Метод Гаусса позволяет решать системы не только с квадратной, но и с прямоугольной матрицей коэффициентов, а также позволяет решать системы, когда определитель матрицы
Ø Перестановка уравнений в системе; Ø Умножение любого уравнения на любое число, отличное от нуля; Ø Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на любое число; Ø Отбрасывание уравнений, в которых все коэффициенты и свободный член равны нулю.
Цель преобразований: Свести матрицу к ступенчатому виду и последовательно, методом обратного хода, начиная с последней строки записать решение системы.
Метод Жордана – Гаусса: Свести исходную систему уравнений к равносильной системе с единичной матрицей коэффициентов.
Пример 1.
Решение (метод Гаусса):
Метод Жордана – Гаусса:
         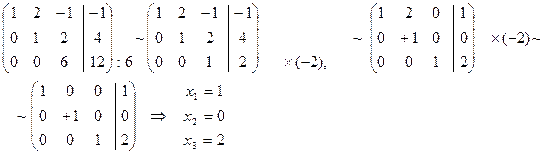
Пример 2.
Решение (Метод Гаусса):
Метод Жордана – Гаусса:
|
||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1020; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

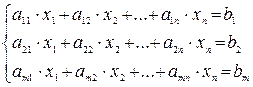
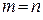
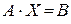 , где
, где 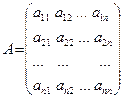 ,
, 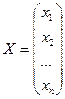 ,
, 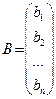
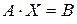
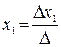 ,
, 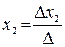 , …,
, …, 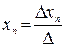 ,
,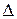 – определитель матрицы коэффициентов системы А, а
– определитель матрицы коэффициентов системы А, а  ,
, 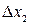 , …,
, …,  – определители замещения, которые получаются, когда в матрице А столбец, содержащий соответствующую переменную, заменяется столбцом свободных членов.
– определители замещения, которые получаются, когда в матрице А столбец, содержащий соответствующую переменную, заменяется столбцом свободных членов.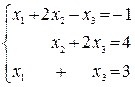
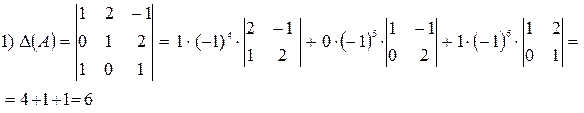


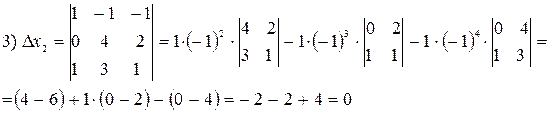
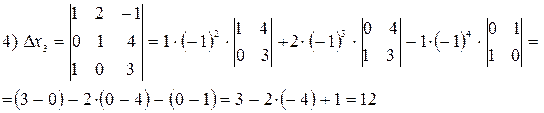
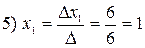 ,
, 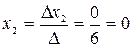 ,
, 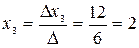
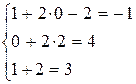
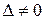 .
.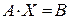
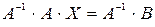
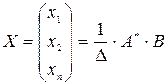
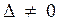 .
.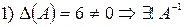
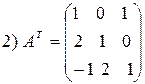
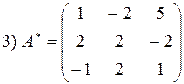
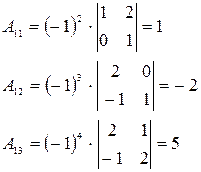
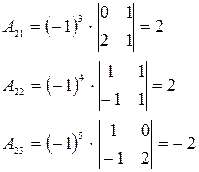
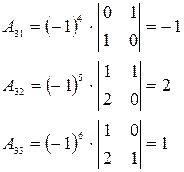
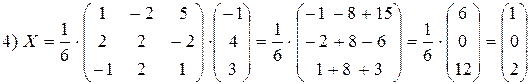
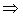
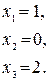
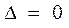 . Метод Гаусса основан на следующих эквивалентных преобразованиях системы уравнений:
. Метод Гаусса основан на следующих эквивалентных преобразованиях системы уравнений: