
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частные производные в экономикеСодержание книги
Поиск на нашем сайте
1. Для функции спроса Q = 70 – 10 ln P а) эластичность спроса от цены; б) перекрестный коэффициент эластичности; в) эластичность спроса от дохода. 2. Известно, что функция спроса Q = P 1) коэффициенты эластичности спроса от цены, альтернативной цены и от дохода. 2) записать выражение для поверхности уровня. 3) цену товара, если при неизменной альтернативной цене доход потребителя удвоится? 4) цену товара, если при неизменном доходе альтернативная цена уменьшится на 30%? 3. Функция спроса Q от цены Р и альтернативной цены Р 1) записать уравнение линии уровня в точке (Р;Р 2) определить величину спроса при условии, что цена Р увеличится, а альтернативная цена одновременно уменьшится на 25%. 4. Построить линии уровня (кривые безразличия) для функции полезности u = 4 Определить предельные полезности в этих точках. 5. Производственная функция задана в виде Q = 8 1) Определить предельные продукты капитала К и труда L. 2) Построить кривые безразличия при Q = 8; 1; и 1/8. 3) При Q = 8 найти коэффициенты заменяемости в точках, где К = 8; 1; 1/8.
Экстремумы
Справочный материал.
1. Точка М (х о, у о) называется точкой максимума (минимума) функции
2. Если в точке максимума или минимума обе частные производные существуют и непрерывны, то они равны нулю в этой точке (необходимое условие экстремума). 3. Если в точке (х о, у о) обе частные производные обращаются в нуль, то характер этой точки определяется величиной При D > 0 имеется экстремум (максимум при А< 0и минимум при А> 0). При D < 0 функция в данной точке не имеет экстремума. При D = 0 вопрос о наличии экстремума остается открытым (достаточное условие экстремума). 4. Наибольшее (наименьшее) значение функции (глобальный максимум (минимум)) 5. Точка М (х о, у о) называется точкой условного максимума (минимума) функции
Уравнение g (x, y) = С называется уравнением связи.
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.255.170 (0.006 с.) |

 + 2,5
+ 2,5 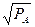 + 0,1Y (Р – цена товара, Р
+ 0,1Y (Р – цена товара, Р  - альтернативная цена, Y – доход потребителя) найти при Р = е, Р
- альтернативная цена, Y – доход потребителя) найти при Р = е, Р 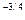 P
P 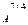 Y
Y 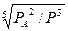 .
.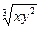 , если x 0 = 1, а y 0 принимает значения: 8; 1; 1/8; 1/64?
, если x 0 = 1, а y 0 принимает значения: 8; 1; 1/8; 1/64?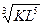 (функция Кобба-Дугласа).
(функция Кобба-Дугласа). Экстремум функции нескольких переменных. Условный экстремум
Экстремум функции нескольких переменных. Условный экстремум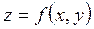 , если существует окрестность точки М, такая, что для всех точек
, если существует окрестность точки М, такая, что для всех точек 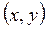 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство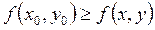
 .
.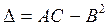 , где
, где 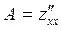 ,
, 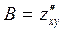 ,
, 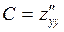 .
.


