
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование выражений, содержащих тригонометрические функцииСодержание книги
Поиск на нашем сайте
Рассмотрим интегрирование некоторых типов выражений, в которых аргумент (1) (2) Приведем примеры на вычисления интегралов указанных типов. Пример 1. Вычислить Решение. Это интеграл типа (1) (при Пример 2. Вычислить Решение. Это интеграл типа (2) (при
Пример 3. Вычислить Решение. Это интеграл типа (1) при
Пример 4. Вычислить Решение. Формально подынтегральное выражение не позволяет данный интеграл отнести к типу (1) или (2). Вот если бы степень синуса или степень косинуса была бы равной 1, то интеграл бы оказался одного из этих типов. Для того, чтобы привести интеграл к нужному типу, воспользуемся основным тригонометрическим тождеством
Рассмотрим теперь интегралы от произведений тригонометрических функций вида
Пример 5. Вычислить Решение. Используем последнюю формулу произведения синуса и косинуса: Рассмотрим теперь вычисление интегралов от четных степеней тригонометрических функций. Для их вычисления используют следующие тригонометрические формулы понижения степени: Пример 6. Вычислить Решение. Используем формулу понижения степени
Пример 7. Вычислить Решение. Используем формулу понижения степени
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.46.108 (0.006 с.) |

 входит только под знаком тригонометрических функций. Прежде всего рассмотрим интегралы вида
входит только под знаком тригонометрических функций. Прежде всего рассмотрим интегралы вида  и
и  . В интеграле
. В интеграле  под
под  понимается любая формула, в которую аргумент
понимается любая формула, в которую аргумент  (где
(где  − некоторое число), причем вся эта формула обязательно под интегралом должна умножаться на
− некоторое число), причем вся эта формула обязательно под интегралом должна умножаться на 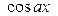 . Аналогично, в интеграле
. Аналогично, в интеграле  понимается любая формула, в которую аргумент
понимается любая формула, в которую аргумент  , но вся эта формула под интегралом умножается на
, но вся эта формула под интегралом умножается на  . Для интегралов вида
. Для интегралов вида  . Найдем дифференциал новой переменной:
. Найдем дифференциал новой переменной:  , откуда
, откуда  . Отсюда следует, что при переходе в интеграле
. Отсюда следует, что при переходе в интеграле 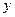 (со связью переменных
(со связью переменных 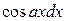 заменить на
заменить на  . Аналогично, легко показать, что при переходе в интеграле
. Аналогично, легко показать, что при переходе в интеграле  ) следует в формуле
) следует в формуле  заменить на
заменить на  . Оформляется это следующей записью:
. Оформляется это следующей записью:
 .
.
 .
.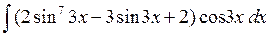 .
. ), поскольку
), поскольку  и есть множитель
и есть множитель  перед
перед  . Тогда по формуле (1):
. Тогда по формуле (1): 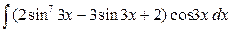


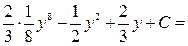 { возвращаемся к старой переменной
{ возвращаемся к старой переменной  , учитывая, что
, учитывая, что  } =
} =  Окончательно:
Окончательно: 

 .
. ), поскольку
), поскольку  входит только в комбинацию
входит только в комбинацию  и есть множитель
и есть множитель  перед
перед 
 {для удобства вносим знак «−» в скобки подынтегрального выражения, меняя знаки в них}=
{для удобства вносим знак «−» в скобки подынтегрального выражения, меняя знаки в них}=  =
= }
}  . Итак,
. Итак, 
 .
. входит только в комбинацию
входит только в комбинацию  и есть множитель
и есть множитель 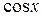 перед
перед 



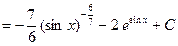 . Окончательно:
. Окончательно:
 .
.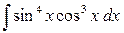 .
. , которое позволяет выразить квадрат одной из тригонометрических функций через другую. Подынтегральная функция:
, которое позволяет выразить квадрат одной из тригонометрических функций через другую. Подынтегральная функция: 
 . Поэтому
. Поэтому  . Теперь видно, что это интеграл вида (1), причем
. Теперь видно, что это интеграл вида (1), причем  , а перед
, а перед  стоит
стоит  . Тогда по формуле (1):
. Тогда по формуле (1): 
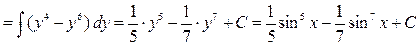 . Таким образом,
. Таким образом,  .
. . Для избавления от произведения под интегралом и превращения его в сумму-разность используются следующие формулы тригонометрии:
. Для избавления от произведения под интегралом и превращения его в сумму-разность используются следующие формулы тригонометрии: ,
,  ,
,  .
. .
. =
= } =
} = 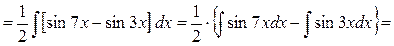
 . Окончательно получаем:
. Окончательно получаем:  .
.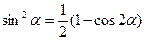 и
и  .
. .
.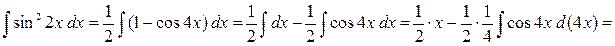
 . Итак,
. Итак,  .
. {раскрываем квадрат суммы}
{раскрываем квадрат суммы} 


 . Окончательно:
. Окончательно: 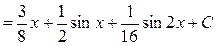 .
.


