
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел VIII. Неопределенный интегралСодержание книги Поиск на нашем сайте
Основные понятия Ранее мы решали следующую задачу дифференцирования (т.е. вычисления производной): дана функция Когда мы по заданной функции вычисляли ее производную, то получали в ответе одну конкретную функцию. То есть для функции ее производная определяется однозначно. Так ли в отношении первообразной? Единственна ли первообразная для данной функции? В первом примере мы убедились, что для функции Теорема. Множество всех первообразных для функции
Множество всех первообразных (ввиду своей важности) получило специальное название и обозначение. Неопределенным интегралом от функции (1) где Правило (*): Для того, чтобы убедиться, что интеграл Какие функции имеют первообразную (а значит, для них существует и неопределенный интеграл)? По крайней мере, таковыми являются все непрерывные функции. Поскольку в самом начале мы уже в примерах находили первообразные для двух функций, то можем уже выписать два интеграла: Таблица (простая) интегралов
Ясно, что можно опять «угадать» интегралы от других основных элементарных функций и составить таблицу интегралов, как в свое время составляли таблицу производных. Назовем ее простой (почему – поймете позже) таблицей интегралов:
7) 11) В этих формулах Таким образом, если необходимо вычислить интеграл от функции, которая есть в этой таблице, то можно просто переписать правую часть соответствующей формулы. В следующих примерах отметим некоторые особенности использования наиболее часто применяющейся табличной формулы 3)
Пример 1. Пусть число
Пример 2. Пусть число
Пример 3. Пусть число
Пример 4. Пусть число
Если же под знаком интеграла стоят суммы-разности функций из таблицы, умноженных на некоторые числа, то для взятия интеграла используют свойства интегралов, излагаемые в следующем параграфе.
|
||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 359; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.188.152 (0.01 с.) |

 , по ней мы строили другую функцию, которая называлась производной данной функции и обозначалась
, по ней мы строили другую функцию, которая называлась производной данной функции и обозначалась  или
или  . Построенная функция оказалась очень полезной для исследования характера зависимости переменных
. Построенная функция оказалась очень полезной для исследования характера зависимости переменных  и
и  , выраженного исходной функцией. Поставим теперь обратную задачу − по известному выражению для производной функции найти саму функцию. Более точно: дана функция
, выраженного исходной функцией. Поставим теперь обратную задачу − по известному выражению для производной функции найти саму функцию. Более точно: дана функция  , а необходимо найти такую функцию
, а необходимо найти такую функцию  , производная которой равна
, производная которой равна  если
если  для всех
для всех 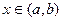 . Далее мы будем опускать упоминание об интервале
. Далее мы будем опускать упоминание об интервале 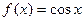 , тогда несложно угадать, что первообразной будет функция
, тогда несложно угадать, что первообразной будет функция  , так как действительно
, так как действительно  . Аналогично, легко проверить, что для функции
. Аналогично, легко проверить, что для функции  первообразной будет функция
первообразной будет функция  .
. ? Возьмем, например,
? Возьмем, например,  . Легко убедиться (взяв производную), что это тоже первообразная для
. Легко убедиться (взяв производную), что это тоже первообразная для  , где
, где  – любое число. Исчерпаем ли мы все первообразные, прибавляя к какой-нибудь из них все числа? Или может найтись такая первообразная, которая не получается из исходной первообразной прибавлением какого-нибудь числа? Оказывается, таких быть не может. И обосновывает этот факт следующая важная
– любое число. Исчерпаем ли мы все первообразные, прибавляя к какой-нибудь из них все числа? Или может найтись такая первообразная, которая не получается из исходной первообразной прибавлением какого-нибудь числа? Оказывается, таких быть не может. И обосновывает этот факт следующая важная . В этом обозначении:
. В этом обозначении:  − значок интеграла,
− значок интеграла,  называется подынтегральной функцией,
называется подынтегральной функцией,  − знак дифференциала (пока пусть это просто буква, разделяющая выражение для подынтегральной функции и переменную интегрирования),
− знак дифференциала (пока пусть это просто буква, разделяющая выражение для подынтегральной функции и переменную интегрирования),  (за буквой
(за буквой  ,
,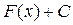 . Как узнать, правильный ли получился ответ, что
. Как узнать, правильный ли получился ответ, что  ? Для проверки можно использовать правило, которое мы фактически сформулировали выше, и которое будем называть
? Для проверки можно использовать правило, которое мы фактически сформулировали выше, и которое будем называть ,
,  .
. 2)
2)  3)
3) 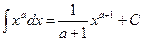 ,
, 
 5)
5)  6)
6) 
 8)
8)  9)
9)  10)
10) 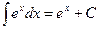
 12)
12)  13)
13) 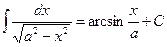

 и
и  – любое (а в формуле 9 – положительное) число.
– любое (а в формуле 9 – положительное) число. .
.
 .
.
 .
.


