Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория приближения функций одной вещественной переменнойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Теория приближения функций одной вещественной переменной Интерполяция алгебраическими многочленами Постановка задачи интерполяции Пусть для функции
Далее будем считать, что выполнено условие
Задача приближенного вычисления для заданной таблицы (1.1) значения функции Решение этой задачи можно найти следующим образом: строится алгебраический многочлен степени не выше
принимающий в точках
Интерполяционным многочленом (интерполянтой) для таблицы (1.1) называется многочлен (1.2) степени не выше Вычисление значения
называется интерполяцией функции Замечание 1.1.. Если Замечание 1.2. Существуют различные формы записи интерполяционного многочлена. Теорема 1.1. Для таблицы (1.1) интерполяционный многочлен существует и единственен. Доказательство. Запишем интерполяционный многочлен в виде
Из условия (1.3) получим систему линейных алгебраических уравнений относительно коэффициентов интерполяционного многочлена
Так как
Следовательно, для любой таблицы (1.1) можно построить единственный интерполяционный многочлен (его коэффициенты определяются единственным решением системы (1.5)). Теорема доказана. Важное замечание 1.1. Наиболее общим способом решения задачи интерполяции для таблицы (1.1) является линейное интерполирование: интерполянт разыскивается в виде обобщенного полинома - линейной комбинации заданной системы линейно независимых базисных функций
где коэффициенты
В этом случае для определения коэффициентов
В силу линейной независимости базисных функций Для случая, когда интерполянт является интерполяционным многочленом система базисных функций имеет вид
Для периодической функции
Такая интерполяция называется тригонометрическо й. В этом случае интерполянт – тригонометрический полином степени
Предложение 1.1. Пусть
Задание. Докажите предложение 1.1. Замечание 1.3. Решение системы (1.5) является достаточно сложной вычислительной задачей. Поэтому способом построения интерполяционного многочлена, установленным при доказательстве теоремы 1.1, на практике обычно не пользуются. Более удобный способ построения интерполяционного многочлена был предложен Лагранжем. Погрешность интерполяции Погрешностью интерполяции называется разность
Очевидно, что в узлах интерполяции
В остальных точках погрешность интерполяции, вообще говоря, отлична от нуля. Замечание 1.6. Из предложения 1.1 следует, что погрешность интерполяции Найдем погрешность интерполяции для многочлена степени В этом случае Следовательно,
где Продифференцировав по
так как Отсюда найдем
Однако, для произвольной функции, заданной только таблицей (1.1), ничего конкретного сказать о погрешности интерполяции нельзя. Если функция Теорема 1.2. Если
где Доказательство. Будем разыскивать погрешность интерполяции в виде (1.9), положив
Зафиксируем произвольное
Очевидно, что Таким образом, Учитывая, что для любого
получаем
Следовательно,
и
Теорема доказана. Важное замечание 1.2. Из формулы (1.11) следует, что погрешность интерполяции зависит от выбора узлов интерполяции Замечание 1.7. Из доказательства теоремы 1.1 получаем, что
Следствие 1.2. Пусть
Важный пример (погрешность линейной полиномиальной интерполяции). Пусть
Наибольшее значение Отсюда по формуле (1.13) получаем максимальную оценку погрешности линейной интерполяции
Если Найдем оценку погрешности интерполяции при минимальных требованиях к гладкости функции Пусть
Действительно, используя формулу (1.15), имеем
Поскольку
Так как
Оценка (1.17) доказана. Если имеется таблица большого числа значений некоторой функции
Замечание 1.8. Для класса Многочлены Чебышова
Рассмотрим поведение многочлена Чебышова Положим в формуле (1.35) Получим
или
Итак, значения многочлена Отсюда получаем, что
Предложение 1.3. Корни многочлена Чебышова Вопрос о корнях многочлена Функция
Отрезку
Предложение 1.3 доказано. Замечание 1.12. Нули функции Предложение 1.4. Многочлен Чебышова
Действительно, производная Предложение 1.4 доказано. Важное замечание 1.6. Многочлены Чебышова
Формула (1.40) получается из (1.35) с помощью обратной замены С помощью (1.40) легко вычисляются значения многочлена Чебышова на отрезке Замечание 1.13. Из формулы (1.40) немедленно получаем: 1) Все многочлены 2) Для
3) Многочлены
Теорема 1.3. Многочлен Чебышова Это означает, что для любого многочлена
Доказательство. Пусть существует многочлен
Тогда разность
Это означает, что многочлен Теорема 1.3 доказана. Таким образом, для решения задачи об оптимальном выборе узлов интерполяции на отрезке
При этом в соответствии с (1.37) оценка погрешности интерполяции (1.12) примет вид
Из теоремы 3 следует, что оценку (1.41) улучшить на отрезке Рассмотрим случай интерполирования на произвольном отрезке
взаимно однозначно отображается на отрезок
Точки (1.43) являются оптимальными узлами для оценки погрешности интерполяции на произвольном отрезке По узлам (1.43) построим
Отсюда получаем оценку погрешности интерполяции на произвольном отрезке
Интерполяционный процесс. Чтобы построить интерполяционный процесс нужно задать на
где все элементы Набор узлов интерполяции По каждой сетке
Последовательность интерполяционных многочленов (2.1) называют интерполяционным процессом. Говоря о сходимости интерполяционного процесса, ищут ответ на вопрос о сходимости последовательности интерполяционных многочленов Интерполяция сплайнами Понятие сплайна. Построенный нами в предыдущем пункте локальный интерполянт Термин сплайн (англ.- spline) имеет техническое происхождение. Первоначально сплайнами называли длинные гибкие деревянные рейки, используемые английскими кораблестроителями для вычерчивания деталей корпуса корабля в натуральную величину. Другими словами, сплайн был чертежным инструментом для построения гладких кривых. В вычислительной математике под сплайном на отрезке Пусть отрезок
Набор точек Сплайном степени
степени не выше Из определения следует, что для многочленов (3.14), представляющих сплайн на каждом частичном отрезке
Таким образом, сплайн – это функция, склеенная из многочленов
Для сплайнов степени
где число Сплайн называется интерполяционным для заданной таблицы (1.1), если
где Интерполяция посредством сплайнов называется сплайн-интерполяцией. Замечание 3.2. Непрерывная кусочно-линейная функция (ломаная) является сплайном первой степени нулевого порядка (дефект равен 1). На практике чаще всего используются сплайны третьей степени второго порядка. Такие сплайны называют кубическими. Выбор значения гладкости
Теория приближения функций одной вещественной переменной
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 518; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.043 с.) |

 ,
,  известны ее значения в
известны ее значения в  - ой точках
- ой точках  . Запишем эти значения функции
. Запишем эти значения функции  в таблицу
в таблицу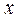



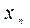


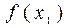

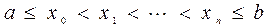 .
. при
при  называется задачей интерполяции (распространения во внутрь).
называется задачей интерполяции (распространения во внутрь).
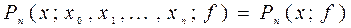 , (1.2)
, (1.2)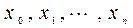 те же значения, что и функция
те же значения, что и функция 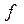 :
: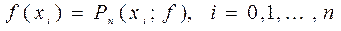 . (1.3)
. (1.3)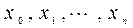 называются узлами интерполяции.
называются узлами интерполяции. по формуле
по формуле (1.4)
(1.4) , то вычисление
, то вычисление 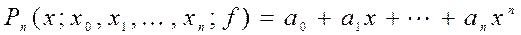 .
. :
: . (1.5)
. (1.5) , то определитель системы (1.5) (определитель Вандермонда) отличен от нуля:
, то определитель системы (1.5) (определитель Вандермонда) отличен от нуля:
 .
.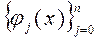 :
: ,
, определяются из условия интерполяции
определяются из условия интерполяции .
. .
.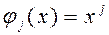 ,
,  .
.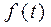 , с периодом
, с периодом  интерполянт разыскивается по системе базисных тригонометрических функций
интерполянт разыскивается по системе базисных тригонометрических функций .
. имеет вид:
имеет вид:
 - пространство многочленов степени не выше
- пространство многочленов степени не выше  , то для любой таблицы (1.1)
, то для любой таблицы (1.1) .
.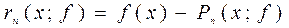 . (1.8)
. (1.8)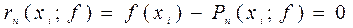 .
. для любой функции
для любой функции  , где
, где 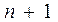 (
( ,
,  ).
). есть многочлен степени
есть многочлен степени 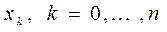 являются его корнями.
являются его корнями. , (1.9)
, (1.9)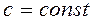 .
. ,
,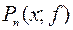 - многочлен степени
- многочлен степени 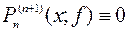 .
. . Таким образом, для
. Таким образом, для  погрешность интерполяции имеет вид
погрешность интерполяции имеет вид . (1.10)
. (1.10) (
( - пространство функций
- пространство функций  ), то для погрешности интерполяции можно получить формулу, аналогичную (1.9).
), то для погрешности интерполяции можно получить формулу, аналогичную (1.9). , то для любого
, то для любого  погрешность интерполяции определяется формулой
погрешность интерполяции определяется формулой , (1.11)
, (1.11) - некоторая точка отрезка
- некоторая точка отрезка  ).
). ,
, .
.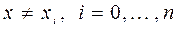 и рассмотрим вспомогательную функцию
и рассмотрим вспомогательную функцию  от переменной
от переменной  :
:
 и обращается в нуль в
и обращается в нуль в  точках отрезка
точках отрезка 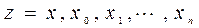 . По теореме Ролля функция
. По теореме Ролля функция  (производная от функции
(производная от функции  ) обращается в нуль, по крайней мере, в
) обращается в нуль, по крайней мере, в  точках отрезка
точках отрезка  , функция
, функция  равна нулю по крайней мере в
равна нулю по крайней мере в  точках этого отрезка,
точках этого отрезка, 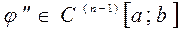 и так далее.
и так далее.
 обращается в нуль, по крайней мере, в одной точке
обращается в нуль, по крайней мере, в одной точке 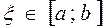 и
и  .
.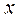
 и
и 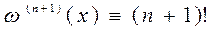 ,
, .
.
 , где
, где  .
. .
.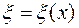 удовлетворяет условию
удовлетворяет условию .
. и
и 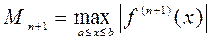 . Тогда
. Тогда , для любого
, для любого  , (1.12)
, (1.12) , (1.13)
, (1.13) (1.14)
(1.14)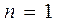 и
и  . Обозначим
. Обозначим  ,
, 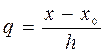 ,
,  . В этом случае
. В этом случае  и интерполяционный многочлен может быть записан в виде
и интерполяционный многочлен может быть записан в виде (1.15)
(1.15) на отрезке
на отрезке  достигается в точке
достигается в точке  и
и 
 . (1.16)
. (1.16) то, оценка (1.16) не имеет места.
то, оценка (1.16) не имеет места.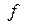 удовлетворяет условию Липшица на отрезке
удовлетворяет условию Липшица на отрезке  , то есть для любых
, то есть для любых  выполнено неравенство
выполнено неравенство  где
где  . Тогда максимальная оценка погрешности линейной интерполяции имеет вид
. Тогда максимальная оценка погрешности линейной интерполяции имеет вид . (1.17)
. (1.17)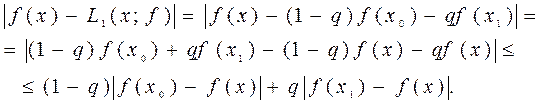
 и
и 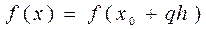 имеем
имеем ,
, .
.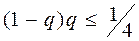 при
при  , то
, то .
. с постоянным шагом
с постоянным шагом  изменения аргумента, то для вычисления значения
изменения аргумента, то для вычисления значения  в заданной точке
в заданной точке 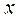 обычно поступают следующим образом. Выбирают два соседних узла, между которыми находится
обычно поступают следующим образом. Выбирают два соседних узла, между которыми находится 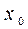 , а правый – за
, а правый – за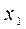 и
и  вычисляют по формуле линейной интерполяции (1.15). Погрешность интерполяции для
вычисляют по формуле линейной интерполяции (1.15). Погрешность интерполяции для  оценивается по формуле (1.16).
оценивается по формуле (1.16). в (1.12)-(1.14) улучшить (уменьшить) нельзя, так как для случая
в (1.12)-(1.14) улучшить (уменьшить) нельзя, так как для случая 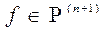 неравенство (1.12) превращается в равенство. Что касается величины
неравенство (1.12) превращается в равенство. Что касается величины  , то она существенно зависит от выбора узлов интерполяции и, следовательно, может быть уменьшена при специальном выборе узлов.
, то она существенно зависит от выбора узлов интерполяции и, следовательно, может быть уменьшена при специальном выборе узлов.

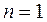








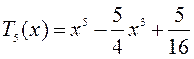
 на отрезке
на отрезке  .
. ,
,  (функция
(функция  взаимно однозначно отображает отрезок
взаимно однозначно отображает отрезок  на отрезок
на отрезок 
 ,
, 
 при
при  на отрезке
на отрезке  (1.37)
(1.37) вещественные, различные и принадлежат интервалу
вещественные, различные и принадлежат интервалу  .
. .
. обращается в нуль в точках
обращается в нуль в точках ,
,  .
. только при
только при 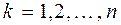 . Следовательно, все
. Следовательно, все  корней многочлена
корней многочлена  (1.38)
(1.38) . Корни многочлена Чебышова в силу нелинейности функции
. Корни многочлена Чебышова в силу нелинейности функции 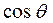 сгущаются к концам отрезка
сгущаются к концам отрезка 
 (1.39)
(1.39) обращается на отрезке
обращается на отрезке  в нуль в точках
в нуль в точках  Точки
Точки 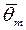 находятся между нулями функции
находятся между нулями функции 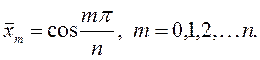
 на отрезке
на отрезке  . (1.40)
. (1.40) при
при  .
. являются четными функциями, а
являются четными функциями, а  нечетными.
нечетными. имеет место рекуррентная формула
имеет место рекуррентная формула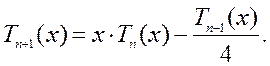
 ,
,  ,
,  :
:
 .
.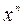 равным 1 имеет на отрезке
равным 1 имеет на отрезке  , такого, что
, такого, что 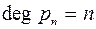 ,
,  имеем
имеем (1.41)
(1.41) , такой, что
, такой, что , (1.42)
, (1.42) ,
,  .
. будет многочленом степени не выше
будет многочленом степени не выше  , отличным от тождественного нуля. Кроме того, в силу (1.37) и предположения (1.40) эта разность в
, отличным от тождественного нуля. Кроме того, в силу (1.37) и предположения (1.40) эта разность в  точках
точках  принимает отличные от нуля значения противоположных знаков:
принимает отличные от нуля значения противоположных знаков: ,
, .
. , то есть точки
, то есть точки (1.43)
(1.43) (1.44)
(1.44) ,
, 
 Отрезок
Отрезок  ,
, 
 на отрезке
на отрезке  на отрезке
на отрезке  ,
, . (1.43)
. (1.43) :
:
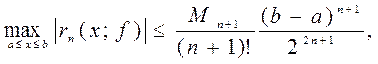 (1.44)
(1.44) .
.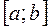 бесконечную матрицу узлов интерполяции
бесконечную матрицу узлов интерполяции
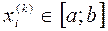 ,
,  ,
,  .
. , принадлежащих
, принадлежащих  , называют сеткой. Таким образом, м атрицаузлов
, называют сеткой. Таким образом, м атрицаузлов  .
.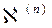 ,
,  можно построить интерполяционный многочлен степени
можно построить интерполяционный многочлен степени 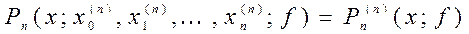 . (2.1)
. (2.1) к функции
к функции  .
. для равноотстоящих узлов, определяемых формулами (3.3)-(3.4), обладает существенным недостатком: в точках склейки - общих точках частичных отрезков
для равноотстоящих узлов, определяемых формулами (3.3)-(3.4), обладает существенным недостатком: в точках склейки - общих точках частичных отрезков  он не является гладкой функцией. Возникает задача построения локального интерполянта, являющегося гладкой функцией на всем отрезке
он не является гладкой функцией. Возникает задача построения локального интерполянта, являющегося гладкой функцией на всем отрезке  . Эта задача решается с помощью сплайнов.
. Эта задача решается с помощью сплайнов. понимают кусочно-полиномиальную функцию гладкую на всем отрезке.
понимают кусочно-полиномиальную функцию гладкую на всем отрезке. частичных отрезков точками
частичных отрезков точками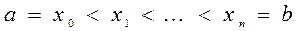 .
. принято называть сеткой.
принято называть сеткой. порядка
порядка  на отрезке
на отрезке  , совпадающая на каждом частичном отрезке
, совпадающая на каждом частичном отрезке  с многочленом
с многочленом (3.14)
(3.14) (3.15)
(3.15)










 Рис. 3.1
Рис. 3.1
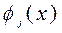 так, что в результате получается
так, что в результате получается  ,
,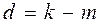 называется дефектом сплайна.
называется дефектом сплайна. , (3.16)
, (3.16) объясняется, в том числе, и тем, что при движении режущего инструмента в автоматизированных металлообрабатывающих комплексах по траектории, являющееся дважды непрерывно дифференцируемой кривой не возникают ударные нагрузки. В случае разрывов второй производной по второму закону Ньютона они появляются и могут привести к разрушению инструмента или дефектам обрабатываемой поверхности. При этом значение степени
объясняется, в том числе, и тем, что при движении режущего инструмента в автоматизированных металлообрабатывающих комплексах по траектории, являющееся дважды непрерывно дифференцируемой кривой не возникают ударные нагрузки. В случае разрывов второй производной по второму закону Ньютона они появляются и могут привести к разрушению инструмента или дефектам обрабатываемой поверхности. При этом значение степени  является минимальным для обеспечения существования интерполяционного сплайна класса
является минимальным для обеспечения существования интерполяционного сплайна класса  для любой таблицы (1.1).
для любой таблицы (1.1).