
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимальный выбор узлов интерполяции. Многочлены ЧебышоваСодержание книги
Поиск на нашем сайте
Формула (1.10) показывает, что погрешность интерполяции зависит от гладкости интерполируемой функции величина Замечание 1.11. Величина Сначала найдем решение задачи об оптимальном выборе узлов интерполяции на отрезке Многочлен Чебышова
Положим Покажем, что формула (1.35) действительно определяет многочлен степени Используя формулу бинома Ньютона, имеем
Отсюда следует, что члены, содержащие иррациональности, при сложении взаимно уничтожаются. Получаем, что выражение (1.35) действительно является многочленом степени Так как,
то коэффициент при старшей степени Многочлены Чебышова
Рассмотрим поведение многочлена Чебышова Положим в формуле (1.35) Получим
или
Итак, значения многочлена Отсюда получаем, что
Предложение 1.3. Корни многочлена Чебышова Вопрос о корнях многочлена Функция
Отрезку
Предложение 1.3 доказано. Замечание 1.12. Нули функции Предложение 1.4. Многочлен Чебышова
Действительно, производная Предложение 1.4 доказано. Важное замечание 1.6. Многочлены Чебышова
Формула (1.40) получается из (1.35) с помощью обратной замены С помощью (1.40) легко вычисляются значения многочлена Чебышова на отрезке Замечание 1.13. Из формулы (1.40) немедленно получаем: 1) Все многочлены 2) Для
3) Многочлены
Теорема 1.3. Многочлен Чебышова Это означает, что для любого многочлена
Доказательство. Пусть существует многочлен
Тогда разность
Это означает, что многочлен Теорема 1.3 доказана. Таким образом, для решения задачи об оптимальном выборе узлов интерполяции на отрезке
При этом в соответствии с (1.37) оценка погрешности интерполяции (1.12) примет вид
Из теоремы 3 следует, что оценку (1.41) улучшить на отрезке Рассмотрим случай интерполирования на произвольном отрезке
взаимно однозначно отображается на отрезок
Точки (1.43) являются оптимальными узлами для оценки погрешности интерполяции на произвольном отрезке По узлам (1.43) построим
Отсюда получаем оценку погрешности интерполяции на произвольном отрезке
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 1104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.208.127 (0.008 с.) |

 (
(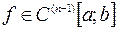 ) и выбора узлов
) и выбора узлов  . Естественно возникает задача нахождения такого расположения узлов интерполяции
. Естественно возникает задача нахождения такого расположения узлов интерполяции 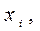
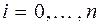 на отрезке
на отрезке 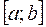 , при котором минимальна
, при котором минимальна и тем самым минимальна правая часть оценки погрешности интерполяции (1.12). Эта задача называется задачей об оптимальном выборе узлов интерполяции.
и тем самым минимальна правая часть оценки погрешности интерполяции (1.12). Эта задача называется задачей об оптимальном выборе узлов интерполяции.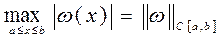 называется в конструктивной теории функций уклонением функции
называется в конструктивной теории функций уклонением функции 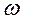 от нуля на отрезке
от нуля на отрезке  .
. . Для этого нам понадобятся многочлены Чебышова.
. Для этого нам понадобятся многочлены Чебышова. для
для 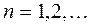 определяется формулой
определяется формулой . (1.35)
. (1.35)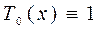 .
. с коэффициентом при старшей степени равным 1.
с коэффициентом при старшей степени равным 1. ,
,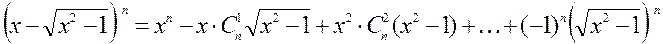 .
.
 многочлена
многочлена 

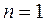








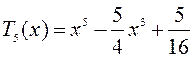
 ,
,  (функция
(функция  взаимно однозначно отображает отрезок
взаимно однозначно отображает отрезок  на отрезок
на отрезок 
 ,
, 
 при
при  на отрезке
на отрезке  (1.37)
(1.37) вещественные, различные и принадлежат интервалу
вещественные, различные и принадлежат интервалу  .
. .
. обращается в нуль в точках
обращается в нуль в точках ,
,  .
. только при
только при 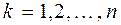 . Следовательно, все
. Следовательно, все  (1.38)
(1.38) . Корни многочлена Чебышова в силу нелинейности функции
. Корни многочлена Чебышова в силу нелинейности функции 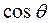 сгущаются к концам отрезка
сгущаются к концам отрезка 
 (1.39)
(1.39) обращается на отрезке
обращается на отрезке  в нуль в точках
в нуль в точках  Точки
Точки 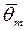 находятся между нулями функции
находятся между нулями функции 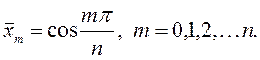
 на отрезке
на отрезке  . (1.40)
. (1.40) при
при  .
. являются четными функциями, а
являются четными функциями, а  нечетными.
нечетными. имеет место рекуррентная формула
имеет место рекуррентная формула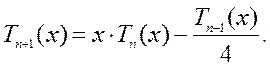
 ,
,  ,
,  :
:
 .
.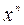 равным 1 имеет на отрезке
равным 1 имеет на отрезке  , такого, что
, такого, что 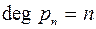 ,
,  имеем
имеем (1.41)
(1.41) , такой, что
, такой, что , (1.42)
, (1.42) ,
,  .
. будет многочленом степени не выше
будет многочленом степени не выше  , отличным от тождественного нуля. Кроме того, в силу (1.37) и предположения (1.40) эта разность в
, отличным от тождественного нуля. Кроме того, в силу (1.37) и предположения (1.40) эта разность в  точках
точках  принимает отличные от нуля значения противоположных знаков:
принимает отличные от нуля значения противоположных знаков: ,
, .
. , то есть точки
, то есть точки (1.43)
(1.43) (1.44)
(1.44) ,
, 
 Отрезок
Отрезок  ,
, 
 на отрезке
на отрезке  на отрезке
на отрезке  ,
, . (1.43)
. (1.43) :
:
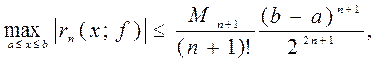 (1.44)
(1.44) .
.


