
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерполяционный многочлен НьютонаСодержание книги Поиск на нашем сайте Удобным представлением интерполяционного многочлена для практических вычислений является его запись в виде интерполяционного многочлена Ньютона. Введем в рассмотрение разделенные разности функции Значения функции Для любой пары узлов
будем называть разделенными разностями первого порядка. Разделенной разностью второго порядка на узлах
Если известны разделенные разности
Заметим, что для построения разделенной разности не обязательно соседство узлов, важно их количество: для разделенной разности Далее мы будем рассматривать разделенные разности, построенные по соседним узлам
Для таблицы (1.1) можно построить таблицу разделенных разностей:
Предложение 1.2. Для разделенной разности
Доказательство предложения 1.2 проведем по индукции. Действительно, разделенная разность первого порядка очевидно может быть представлена в виде (1.18):
Пусть формула (1.18) справедлива для разделенных разностей
Подставляя сюда вместо разделенных разностей
Предложение 1.2 доказано. Из предложения 1.2 (формулы (1.18)) получаем следующие важные свойства разделенных разностей: 1) Разделенная разность является линейным оператором относительно функции 2) Разделенная разность 3) Погрешность интерполяции
Действительно, имеем
Выражение в фигурных скобках совпадает с представлением разделенной разности Формула (1.19) доказана. 4) Если
где
Действительно из следствия 3) из предложения 1.2 для любого
С другой стороны, по теореме 1.2 для любого
где Замечание 1.9. Если Отсюда следует, что если Полученные результаты позволяют записать интерполяционный многочлен для таблицы (1.1) в виде
Действительно, имеет место очевидное равенство:
где Из очевидного равенства
Следует, что многочлен По следствию 2) из предложения 1.2 имеем
где Пусть
Так как
и, следовательно,
Формула (1.21) доказана. Явная запись интерполяционного многочлена для таблицы (1.1) в виде (1.21) называется интерполяционной формулой Ньютона, а полином Важное замечание 1.3. Интерполяционную формулу Ньютона можно считать дискретным аналогом формулы Тейлора. При этом она не содержит производных и ее погрешность (1.19) напоминает остаточный член формулы Тейлора. Достоинством записи интерполянта в форме Ньютона является то, что для повышения степени интерполяционного многочлена нет необходимости в его полной перестройке; достаточно лишь добавить к уже полученному выражению еще одно или несколько слагаемых. Кроме того, с помощью разделенных разностей можно приближенно оценивать погрешность интерполяции.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 908; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 для заданной таблицы (1.1).
для заданной таблицы (1.1). будем называть разделенными разностями нулевого порядка.
будем называть разделенными разностями нулевого порядка. величины
величины
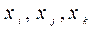 назовем величину
назовем величину
 - ого порядка, то разделенная разность
- ого порядка, то разделенная разность  - ого порядка на узлах
- ого порядка на узлах 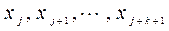 определяется как
определяется как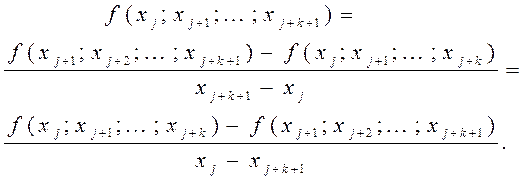
 узел.
узел. ,
,  :
:

 -ого
порядка
-ого
порядка
 -ого
порядка
-ого
порядка




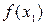



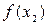

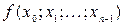


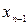



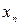



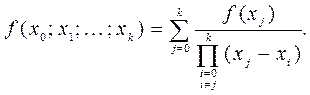 (1.18)
(1.18)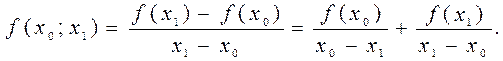
 - ого порядка. Тогда по определению
- ого порядка. Тогда по определению

 является симметрической функцией своих аргументов
является симметрической функцией своих аргументов  представима формулой
представима формулой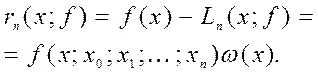 (1.19)
(1.19)
 - ого порядка
- ого порядка  по формуле (1.18).
по формуле (1.18).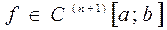 , то
, то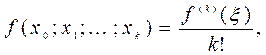 (1.20)
(1.20) ,
, 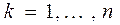 .
. имеем
имеем .
.

 . Следовательно,
. Следовательно, 
 . Полагая здесь
. Полагая здесь  , получаем следствие 4).
, получаем следствие 4). - многочлен степени
- многочлен степени  {
{ 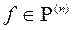 ,
,  }, то для любого
}, то для любого 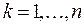 разделенная разность
разделенная разность  -ого порядка
-ого порядка  есть многочлен степени
есть многочлен степени  .
. тождественно равна нулю.
тождественно равна нулю. :
: (1.21)
(1.21)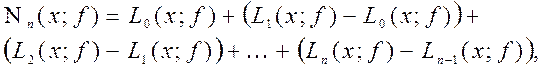
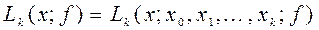 ,
,  - интерполяционный многочлен Лагранжа степени
- интерполяционный многочлен Лагранжа степени  , построенный по узлам
, построенный по узлам  таблицы (1.1).
таблицы (1.1). ,
, 
 является интерполяционным для многочлена
является интерполяционным для многочлена  .
.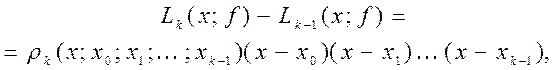
 - разделенная разность
- разделенная разность  .
.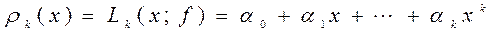 . Из следствия 3) предложения 1.2 получаем, что для любого
. Из следствия 3) предложения 1.2 получаем, что для любого  разделенная разность
разделенная разность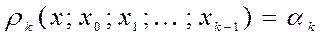 .
. при
при  , то при
, то при  , имеем
, имеем

 - интерполяционным многочленом Ньютона (полиномом Ньютона).
- интерполяционным многочленом Ньютона (полиномом Ньютона).


