
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сходимость интерполяционного процесса.Содержание книги Поиск на нашем сайте Обычно рассматривают следующие виды сходимости функциональной последовательности 1) Поточечная сходимость к
2) Равномерная сходимость к
3) Среднеквадратичная сходимость с весом
В дальнейшем нам понадобится важный результат линейного функционального анализа, известный как теорема Банаха-Штейнгауса. Пусть Теорема 2.1. (Банах-Штейнгаус) Для того чтобы последовательность операторов
необходимо и достаточно выполнение двух условий: а) существует б) последовательность Важное замечание 2.1. Для матрицы узлов
Введем оператор Положим
где Нетрудно доказать, что
Следовательно,
В противном случае нормы операторов Замечание 2.1. С практической точки зрения интересны два случая сходимости интерполяционного процесса на равномерных сетках (сетках с равноотстоящими узлами): 1) Пусть 2) Пусть Случай 1) для Что касается случая 2), то увеличение числа узлов, то есть степени интерполяционного многочлена В общем случае свойство сходимости или расходимости интерполяционного процесса зависит как от выбора на Приведем некоторые результаты, иллюстрирующие этот вывод. Теорема 2.2. (Фабер-Бернштейн) Для любой последовательности сеток
Теорема 2.3. (Марцинкевич) Для любой непрерывной на
Теорема 2.4. Если
Пример. (Бернштейн)Если
не будут сходиться при
Замечание 2.2. Если в предыдущем примере равномерную сетку заменить чебышовской сеткой
Среднеквадратичнуюсходимость с весом последовательности интерполяционных многочленов Предложение 2.1. Пусть
Важное замечание 2.2. В практических вычислениях интерполяционные многочлены высокой степени (
|
||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 781; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.005 с.) |

 для фиксированной последовательности сеток
для фиксированной последовательности сеток  :
: на
на 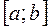 :
: для любого
для любого  ;
;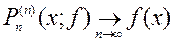 на
на  ;
; на
на  к
к  ;
; на
на  - произвольное банахово пространство. Рассмотрим последовательность линейных непрерывных (ограниченных) операторов
- произвольное банахово пространство. Рассмотрим последовательность линейных непрерывных (ограниченных) операторов  .
. поточечно сходилась к оператору
поточечно сходилась к оператору  при
при  , то есть
, то есть при
при  ,
, (
( ) такая, что
) такая, что  для всех
для всех  .
.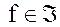 , где
, где 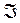 - плотное множество в банаховом пространстве
- плотное множество в банаховом пространстве 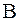 .
. на
на 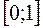 построим последовательность интерполяционных многочленов Лагранжа
построим последовательность интерполяционных многочленов Лагранжа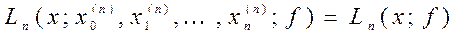 .
. (
( - пространство функций непрерывных на
- пространство функций непрерывных на  ,
,  ), ставящий в соответствие функции
), ставящий в соответствие функции  .
. ,
,
 - многочлены базиса Лагранжа (см. (1.6)).
- многочлены базиса Лагранжа (см. (1.6)). . С другой стороны имеет место неравенство (Бернштейн)
. С другой стороны имеет место неравенство (Бернштейн) (2.1)
(2.1) , при
, при  . Отсюда и теоремы 2.1 получаем, что последовательность
. Отсюда и теоремы 2.1 получаем, что последовательность  не может сходиться равномерно на
не может сходиться равномерно на  :
: .
. были бы по условию а) теоремы 2.1 ограничены.
были бы по условию а) теоремы 2.1 ограничены. фиксировано (
фиксировано ( ). В этом случае рассматривается сходимость интерполяционного процесса при
). В этом случае рассматривается сходимость интерполяционного процесса при  на последовательности сеток
на последовательности сеток 
 фиксировано (
фиксировано ( ). В этом случае рассматривается сходимость интерполяционного процесса при
). В этом случае рассматривается сходимость интерполяционного процесса при 
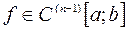 рассмотрен в пункте 1.5. (см. формулы (1.22) и (1.24)). Мы отметили, что погрешность интерполяции есть величина порядка
рассмотрен в пункте 1.5. (см. формулы (1.22) и (1.24)). Мы отметили, что погрешность интерполяции есть величина порядка  при
при  с ростом ее порядка и функция
с ростом ее порядка и функция  может вообще иметь только ограниченное число производных.
может вообще иметь только ограниченное число производных. матрицы узлов
матрицы узлов 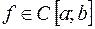 ) найдется такая последовательность сеток
) найдется такая последовательность сеток 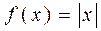 ,
,  , то интерполяционные многочлены
, то интерполяционные многочлены 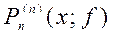 , построенные на равномерных сетках
, построенные на равномерных сетках ,
, к
к  ни в одной точке, кроме
ни в одной точке, кроме  :
: на
на  .
. (сеткой, построенной по узлам, являющимся корнями многочлена Чебышова
(сеткой, построенной по узлам, являющимся корнями многочлена Чебышова  ), то интерполяционные многочлены
), то интерполяционные многочлены  на
на  :
: на
на  .
.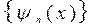 - система многочленов, ортогональных на
- система многочленов, ортогональных на  - корни многочлена
- корни многочлена  . Тогда для последовательности сеток
. Тогда для последовательности сеток  соответствующая последовательность интерполяционных многочленов
соответствующая последовательность интерполяционных многочленов  сходиться при
сходиться при  ) обычно не используются. Для интерполяции заданной функции
) обычно не используются. Для интерполяции заданной функции 


