
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция распределения. ГистограммаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Цель работы. Студент должен знать: смысл первичной статистической обработки результатов исследований, параметры и способы распознания различных типов распределения случайных величин. Студент должен уметь: произвести первичную статистическую обработку результатов экологических экспериментов, произвести построение гистограмм. Практическое значение выполняемых исследований Количественные закономерности в природе и технике могут быть изучены с использованием методов математической статистики. Таким образом может быть выполнен анализ основных погрешностей в различных измерениях с использованием простейших методов статистической обработки результатов экологических и биологических измерений. Использование программ в языках программирования (например, BASIC) для нахождения различных статистических характеристик и обработки результатов позволяет резко облегчить механические многократно повторяемые операции в расчетах и повысить их точность. Литература 1. Еськов В.М., Филатова О.Е., Рачковская В.А. Статистическая обработка результатов измерений в практикуме по экологии и естествознанию.- Сургут: Изд. СурГУ, 1999.- 43 с. 2. М. Дж. Кендалл, А. Стюарт. Теория распределений. 3. Гмурман В. В.. Теория вероятностей и математическая статистика.
Бюджет времени: На изучение темы отводится 6 часов, из них 2 часа лекций, 2 часа лабораторные занятия и 2 часа на самоподготовку.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО I ЭТАПУ "Самоподготовка" Для подготовки к лабораторной работе Вам следует повторить материал прошлых курсов, изучить лекции и ответить на следующие вопросы: 1. Каков смысл статистической обработки результатов? 2. Сформулируйте теорему Бернулли. 3. Что такое случайная величина? Назовите величины ее характеризующие. 4. В чем отличие распределения Гаусса от распределения Пуассона? 5. Как осуществляется поиск грубых ошибок (промахов) эксперимента? 6. Сформулируйте алгоритм поиска ошибки эксперимента.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО II ЭТАПУ: “Выполнение лабораторной работы” 1. Отранжируйте ряд с экспериментальными данными (получите их у преподавателя) и разбейте его на 5-7 интервалов. 2. Рассчитайте 3. Постройте гистограмму: по вертикале 4. Сравните график с функцией Гаусса и сделайте вывод. Блок информации Классическое и статистическое определение вероятности. Теорема Бернулли
В природе, технике, и особенно в различных естественных науках (которые раньше называли физикой), при проведении различных наблюдений и исследований человек имеет дело с различными величинами, которые мы в дальнейшем будем называть эколого-техническими величинами (ЭТВ), выделяя специфику рассматриваемого вопроса. Вообще под физикой можно понимать все природные явления (от первоначального понятия physic- природа). Эти величины могут быть абсолютными константами (например, скорость света С), относительными константами для данных исследований (например, скорость движения тела- постоянная величина в данном эксперименте), а также переменными ЭТВ, зависимыми или независимыми (рост и масса учащихся в школе №). Как известно, в природе зависимости между переменными величинами могут быть функциональными, когда одному или нескольким значениям независимых величин xi соответствует вполне определенное значение зависимой величины y, т.е. y=y(x1,x2,...xn) и статистическими, когда одному значению переменной x соответствует целая совокупность (так называемый ряд распределения) другой переменной y. В последнем случае мы будем говорить о влиянии различных случайных факторов на изучаемые физические процессы, в которых, однако, можно установить вполне конкретные, статистические закономерности. Строго говоря, случайные факторы действуют в любом экологическом или техническом эксперименте, где точность измерительных приборов невысока, а исключить влияние других природных факторов (колебания температур, освещенности, вибрации) представляется невозможным. Отсюда следует целесообразность и необходимость элементарных знаний по статистической обработке результатов измерений у исследователей при выполнении измерений в естествознании и биологии, в частности, довольно часто в методической литературе статистическую обработку сводят к расчетам погрешностей, но, как мы убедимся, круг задач, возникающих при выполнении эколого-технических измерений, значительно шире и требует более глубоких знаний в области математической статистики. Однако, несмотря на большое разнообразие возникающих статистических задач, следует еще раз подчеркнуть главную идею при обработке результатов измерений- установление вполне определенных закономерностей между изучаемыми ФТВ. Рассмотрение темы начнем с наиболее общего и простейшего раздела - построение гистограмм и расчета погрешностей или ошибок измерений. Конечной целью многих исследований является нахождение истинного значения ЭТВ (концентрация токсичных веществ в оде или воздухе, скорость прироста численности популяции, отношения половозрелых и неполовозрелых особей в популяции, продолжительность жизни жителя ХМАО и т.д.) или совокупности истинных значений переменных при изучении и проверке законов природы. Эти истинные значения ЭТВ (в дальнейшем будем обозначать xo или yo) можно найти практически, если воспользоваться известной теоремой теории вероятностей - теоремой Бернулли, которая гласит, что частота любого события P* (отношение числа испытаний, в которых событие наступило m к общему числу испытаний n, т.е.
P* =m/n (8.1) сходится по вероятности к вероятности P этого события. Иными словами при неограниченном числе испытаний мы с очень большой точностью можем определить истинное значение Р исследуемой величины. Например, проводя эколого-технические измерения бесконечно большое число раз и получая значения нашей ЭТВ x1,x2,...xn, где n®¥, мы можем вычислить среднее значение
которое при n®¥ будет с очень большой вероятностью
где e- любое сколь угодно малое положительное число. Отметим, что вероятность достоверного (происходящего в любом испытании) события- P=1, а невозможного события- P=0. В указанном методе нахождения xo имеются определенные сложности. Во- пеpвых, бесконечно много раз повторять эксперимент вообще говоря бессмысленно. Во- втоpых, рассуждения справедливы, если отклонения Dx (или ошибки) измеряемой ЭТВ x от xo (Dx=x-xo) являются так называемыми случайными величинами (СВ) или случайными ошибками, которые не зависят от экспериментатора и их невозможно исключить, а можно только учитывать. Практически, исследователь может допустить еще два вида ошибок: промахи и систематические ошибки. Промахи происходят при неаккуратном выполнении измерений или вследствие незнания исследователем порядка выполнения работ, ее целей и задач. Эти ошибки могут и должны быть исключены путем перехода от незнания к знаниям. Систематические ошибки есть результат действия некоторых постоянных факторов, которые можно выявить и исключить. Примерами таких ошибок являются: действие выталкивающей силы Архимеда при взвешивании на аналитических весах, наличие теплового расширения шкал измерительных приборов (например, термометров), неправильная установка нуля прибора и т.д. Для измерительных приборов со шкалой всегда указывается класс точности прибора, который равен относительной ошибки в процентах (т.е. отношению абсолютной погрешности прибора Dx в делениях к общему числу делений на шкале x), определяемой как:
Это значит, если класс точности равен 2 и общее число делений на шкале x=200, то (Dx/x)•100%=2. Отсюда Dx=2x/100%=400/100=4 (делениям). Тогда при показаниях прибора 40 делений относительная погрешность измерения составит Z:
так как 4 делениям погрешности по отношению к измеряемым 40 дают 10% погрешности. Таким образом, чем меньше измеряемая величина x, тем выше относительная погрешность измерения. Значит измерять надо во второй половине шкалы приборов!
 , в который с некоторой заданной вероятностью b (доверительной вероятностью) попадает истинное значение xo. Иногда говорят, что полученный доверительный интервал накрывает истинное значение xo с заданной вероятностью b (см. рис. 8.1), т.е. , в который с некоторой заданной вероятностью b (доверительной вероятностью) попадает истинное значение xo. Иногда говорят, что полученный доверительный интервал накрывает истинное значение xo с заданной вероятностью b (см. рис. 8.1), т.е.
Рис. 8.1. Нахождение истинного значения х0 случайной величины и его среднего значения на числовой оси в рамках доверительного интервала.
Для понимания сущности метода расчета доверительного интервала любому исследователю природных явлений необходимо рассмотреть некоторые основные закономерности теории вероятностей (ТВ) и математической статистики (МС), однако, для сугубо практического использования предлагаемых методов приведенную ниже информацию (в 8.7 и 8.8) можно использовать для ознакомления. В заключение важно отметить, что вероятность события легко (классически) определяется только для схемы урн (шансов), когда мы имеем полную группу событий (в результате испытания одно событие обязательно наступит!) и они равнозначны. Тогда P(A)=m/n где m- число шансов (случаев) таких, что событие А наступит, а n- общее число случаев. Например, в карточной колоде 4 туза и всего 36 карт, тогда вероятность вытащить туза (событие А) равна
Р(А)= 4/36= 1/6. Во всех остальных случаях мы должны использовать теорему Бернулли для нахождения Р(А), указывая, что Р*(А)®Р(А) при n®¥, т.е. надо повторять число испытаний для повышения точности идентификации вероятности события A. Для изучения понятия гистограмм мы сейчас должны рассмотреть ряд важнейших понятий: 1. Понятие ряда распределения. 2. Дифференциальная и интегральная функции распределения. 3. Числовые характеристики случайных величин.
1.Случайная величина (СВ) х - переменная, принимающая те или иные значения в результате испытания из множества возможных значений {х}. Если это множество бесконечное и непрерывное, т.е. соответствует определению х на отрезке или прямой, то говорят о непрерывной случайной величине (НСВ), иначе, если множество значений х- дискретный ряд чисел, то говорят о дискретной случайной величине (ДСВ). Каждому значению ДСВ соответствует своя вероятность появления P=P(x), которая связана с частотой события P* предельной теоремой Бернулли (см. выше). Например, возраст особи – НСВ. Численность особей в популяции – ДСВ (хотя иногда мы ее считаем НСВ в 1-й части) При бросании шестигранного кубика один раз, выпадение 5 очков происходит с вероятностью P=1/6, это означает, что при очень большом числе испытаний n, отношение числа испытаний m с выпаданием 5 очков к общему числу испытаний n приближенно равно P, т.е.
Отличие Р от Р* определяется теоремой Бернулли (см. 8.3) Для любой ДСВ можно задать ряд распределения, т.е. таблицу соответствий численных значений х её вероятности. Например, для нашего случая
Этому ряду распределения P=P(x) соответствует график в координатах P и x в виде набора точек, которые можно соединить отрезками. В нашем примере P(xi)=1/6=const (8.8) В термодинамике биосистем (бофизика) в разделе "Энтропия" Вы более подробно познаколись с одной из физических интерпретаций вероятности ДСВ и ее связи с таким фундаментальным понятием, как энтропия и S (забегая вперед, отметим: S~ ln P).
Рис. 8.2. Графическое представление функции распределения Р(х) для ДСВ (опыт с бросанием кубика).
Для НСВ вероятность принятия конкретного значения х всегда равна нулю. На практике это соответствует тому, например, что невозможно изготовить по заданию деталь размером точно 22 мм, т.к. обязательно будет какая-то погрешность. Тогда целесообразно говорить о вероятности попадания х в некоторый интервал Dx около заданного значения x, т.е. хÎ(x±Dx). Очевидно, что эта вероятность P будет зависеть от Dx и самого значения x (см. замечание 1) [1] т.е.
Функция f(x) называется плотностью вероятности или дифференциальным законом распределения случайной величины. Она не отрицательна, определена для всех хÎ(-¥,+¥) и определяет вероятность попадания х внутрь любого интервала (a,b) формулой
В квантовой механике дифференциальная функция распределения может быть получена после решения уравнения Шредингера. Она имеет большой теоретический смысл, т.к. определяет вероятность нахождения частицы (например, электрона) в некоторой области пространства Dv, т.е. Dv=Dx·Dy·Dz. По формуле Ньютона-Лейбница
где F(x) первообразная для f(x), и называется интегральной функцией распределения. Она определяет вероятность того, что случайная величина X примет любые значения меньше данного x (см. замечание 2)[2]. Значения f(x) или F(x) для НСВ полностью ее определяют. На практике же найти эти функции бывает очень сложно и чаще определяют так называемые числовые характеристики (ЧХ) или их статистические величины, которые с заданной степенью точности (вероятностью) приближаются к истинным значениям. В математической статистике существует целый комплекс методов оценки достоверности совпадения практически определённых ЧX и их истинных значений (критерий согласия Пирсона, Колмогорова и т.д.) или даже статистической функции распределения F*(x) и истинной F(x). Отметим, что гистограмма грубо представляет f(x), т.е. она является статистическим аналогом дифференциальной функции распределения. Однако, если известно истинное значение f(x) или F(x), то определить их ЧX несложно. Рассмотрим важнейшие из них. I Математическое ожидание или момент нулевого порядка характеризует среднее значение СВ. Для ДСВ
Для НСВ
Обратите внимание, что сумма переходит в интеграл, а вместо вероятности Pi=P(xi) в формуле (8.13) стоит f(x)dx). II Дисперсия или центральный (относительно среднего значения x) момент второго порядка D[0] характеризует величину разброса значений х около x=M[0]. Для ДСВ
Соответственно для НСВ
Так как по размеру D[0]~x2, то на практике для удобства пользуются средним квадратическим отклонением или стандартом случайной величины
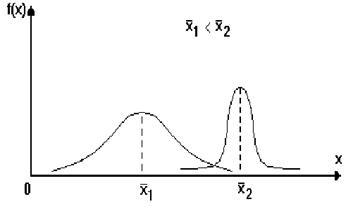
На рис.8.3 приводятся графики плотности вероятности f(x) для т.н. нормального закона распределения (распределения Гаусса) со значениями D1[0]<D2[0], а на рис.8.4 распределения Гаусса с разными M[0]. III Существуют центральные моменты высших порядков, которые характеризуют, например, асимметричность f(x) (момент третьего порядка)
и др. свойства функции f(x). Отметим, что математическое понятие центрального момента в ТВ пришло из механики. Если на прямой находятся точечные массы m1, m2,..., mn и их абсциссы на числовой оси x1,x2,...,xn, то момент первого порядка или статический момент, деленный на
а момент второго порядка
равен моменту инерции системы материальных точек I. В ТВ абсциссам x соответствует значение СВ (ДСВ или НСВ), а аналогом mi/m является вероятность
поэтому последнюю величину Pi в статистике иногда называют относительным весом или просто весом
В природе существуют различные законы распределения СВ, из них наибольшее распространение получили: нормальный закон распределения или закон Гаусса, для которого плотность вероятности равна (см. рис.8.3):
и распределение Пуассона для n целочисленных (дискретных) значений СВ, где n невелико, имеющее вид:
где m - среднее значение случайной величины (см. рис. 8.5). Для задания нормального закона достаточно знать s- среднее квадратическое отклонение и Таким образом, зная эти параметры для некоторой СВ мы имеем полную информацию о ней. Вот почему одной из главных задач статистической обработки результатов экспериментальных измерений (СОРЭИ) является получение хотя бы приближенных значений параметров функций распределений и оценка степени точности вычисленных параметров на основе сравнительно небольшого числа измерений (так называемых малых выборках). Конечная задача СОРЭИ - свернуть статистический ряд (совокупность всех возможных экспериментальных значений х) до одной функции распределения, которая в сжатой форме хранит информацию о данной СВ. В нашей работе это делается через построение гистограмм для измеряемых экологических случайных величин. В заключение приведем графики функции Гаусса.
Рис.8.3. Две функции Гаусса для 2-х различных дисперсий.
Рис.8.4. Две функции распределения Гаусса для 2-х разных значений математического ожидания и двух разных дисперсий (D1>D2).
Отметим при этом, что вероятность попасть случайной величине х в интервал ( График распределения Пуассона имеет следующий вид:
Рис.8.5. График распределения Пуассона.
Это распределение асимметрично и при n®¥ переходит в распределение Гаусса. Остановимся более подробно на практической части – построении гистограмм. По определению: “гистограмма – это график, состоящий из прямоугольников, высота которых равна частоте события 1. Полученную в опыте выборку (всех xi) необходимо ранжировать (расположить в порядке вырастания от xmin до xmax). 2. Разбить весь интервал измерения (xmin, xmax) на m частей ( 3. Для каждого 4. На графике ( 5. Приблизительно соеденить верхушки прямоугольников плавной линией и получить грубый вид f(x) (обратить внимание на схожесть Вашей гистограммы с функцией Гаусса (или др. функцией)).
Лабораторная работа № 9.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 790; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.015 с.) |

 для каждого интервала и запишите в таблицу (
для каждого интервала и запишите в таблицу (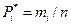 ).
).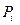 , а по горизонтали
, а по горизонтали 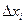 .
. (8.2)
(8.2) приближаться к истинному значению xo, при этом
приближаться к истинному значению xo, при этом 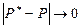 . В этом случае говорят, что Р* сходится к Р по вероятности. Это высказывание аналитически запишется так
. В этом случае говорят, что Р* сходится к Р по вероятности. Это высказывание аналитически запишется так при n®¥, (8.3)
при n®¥, (8.3)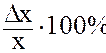 .
. , (8.4)
, (8.4)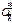
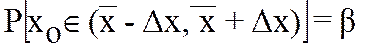 (8.5)
(8.5)
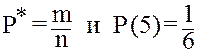 (8.6)
(8.6)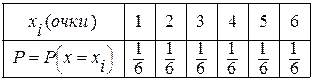 (8.7)
(8.7)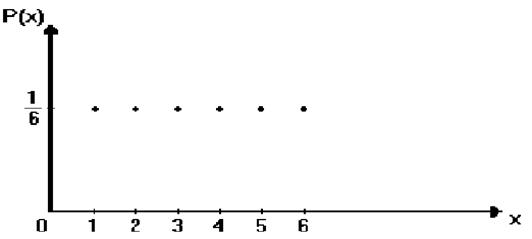
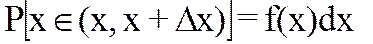 (8.9)1
(8.9)1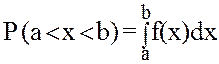 (8.10)
(8.10)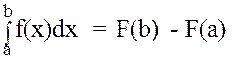 , (8.11)
, (8.11)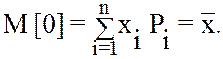 (8.12)
(8.12)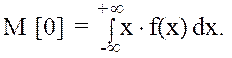 (8.13)
(8.13)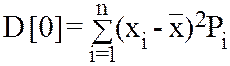 , (8.14)
, (8.14)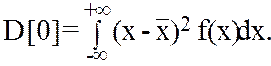 (8.15)
(8.15) (8.16)
(8.16) (8.17)
(8.17)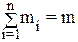 определяет центр массы системы
определяет центр массы системы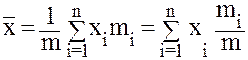 (8.18)
(8.18)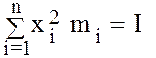 (8.19)
(8.19)
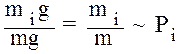 .
.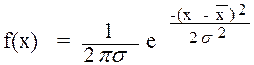 (8.20)
(8.20)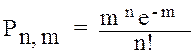 (8.21)
(8.21) (математическое ожидание х). Чтобы определить распределение Пуассона достаточно знать только один параметр m.
(математическое ожидание х). Чтобы определить распределение Пуассона достаточно знать только один параметр m.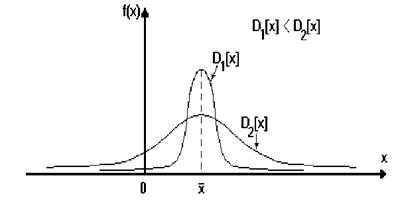
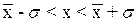 ) равна b=0.6326, а в интервал
) равна b=0.6326, а в интервал 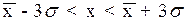 равна b=0.9972, т.е. последняя вероятность соответствует "почти достоверному" событию. Вот почему в математической статистике значение СВ, выходящее за интервал в
равна b=0.9972, т.е. последняя вероятность соответствует "почти достоверному" событию. Вот почему в математической статистике значение СВ, выходящее за интервал в 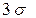 около
около 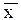 отбрасывают как маловероятные. Использование этого свойства распределения Гаусса получило название " правило трех сигм ".
отбрасывают как маловероятные. Использование этого свойства распределения Гаусса получило название " правило трех сигм ".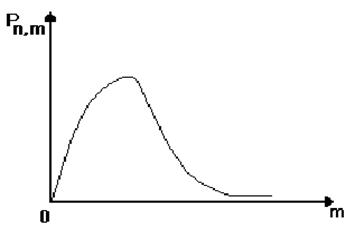
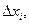 где
где 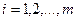 ).
).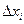 найти свои значения частот
найти свои значения частот 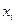 попавшие в
попавшие в 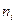 на число N всех измерений, т.е.
на число N всех измерений, т.е. 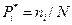 .
.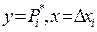 ) построить прямоугольники с высотой
) построить прямоугольники с высотой 


