
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равномерное распределение. Плотность, функция распределения, математическое ожидание и дисперсия.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
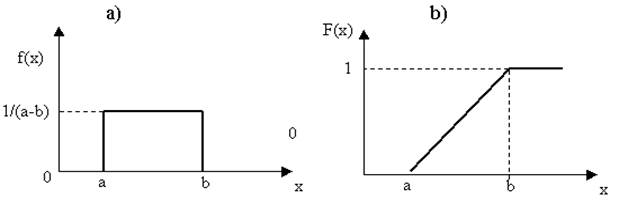
Равномерное распределение. Плотность, функция распределения, математическое ожидание и дисперсия. Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение. Исходя из основного свойства плотности вероятности, f(x) = 1/(b-a) на интервале (a;b). Основное свойство плотности вероятности: несобственный интеграл от плотности вероятности в пределах от -∞ до +∞ равен единице. Геометрически это выражается тем, что площадь фигуры, ограниченной сверху графиком плотности вероятности, снизу - осью OX, равна 1.
Математическое ожидание равномерного распределения: Пусть случайная величина
Математическое ожидание
Дисперсия равна Среднее квадратичное отклонение равномерного распределения:
Двумерная СВ. Задание закона распределения указанной СВ. Кроме одномерных случайных величин изучают величины, возможные значения которых определяются двумя, тремя,…, n числами. Такие величины называются соответственно друмерными, трехмерными,…, n – мерными. Будем обозначать через (X, Y) двумерную случайную величину. Каждую из величин X, Y называют составляющей (компонентой); обе величины X и Y, рассматриваемые одновременно, образуют систему двух СВ. Законом распределения дискретной двумерной СВ называют перечень возможных значений этой величины, т.е. пар чисел Первая строка таблицы содержит все возможные значения составляющей Х, а первый столбец – все возможные значения составляющей Y. В клетке, стоящей на пересечении «столбца Так как события Зная закон распределения двумерной дискретной СВ, можно найти законы распределения каждой из составляющих. Действительно, например события
Функцией распределения двумерной СВ (X, Y) называют функцию F(x,y), определяющую для каждой пары чисел х, у вероятность того, что Х примет значение, меньшее х, и при этом Y примет значение, меньшее у: F(x, y) = P(X< x, Y< y). Свойство 1. Значение функции распределения удовлетворяют двойному неравенству Свойство 2. F(x, y) есть неубывающая функция по каждому аргументу т.е.
Свойство 3. Имеют место предельные соотношения: 1) 2) Свойство 4. a) При y = ∞ функция распределения системы становится функцией распределения составляющей X:
Используя функция распределения системы СВ X и Y, легко найти вероятность того, что в результате испытания случайная точка попадает в полуполосу
Вычитая из вероятности попадания случайной точки в квадрант с вершиной Аналогично имеем
Рассмотрим прямоугольник
Найдем вероятность попадания случайной точки Основные понятия математической статистики: генеральная и выборочная совокупности. Повторная и бесповторная выборки.
Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов. Генеральной совокупностью называют совокупность объектов, из которых производится выборка. При составлении выборки можно поступать двумя способами: после того как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. Выборки подразделяются на повторные и бесповторные. Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность. Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается. 47. Виды представления статистического эксперимента (вариационного ряда): полигон, гистограмма, эмпирическая функция распределения. Простейшее преобразование статистических данных является их упорядочивание по величине. Выборка
Рисунки и графики представляют собой удобный и наглядный способ представления выборки. Выборку, извлеченную из дискретной генеральной совокупности, можно представить в виде полигона частот или полигона относительных частот. На плоскости в прямоугольной системе координат строят точки с координатами
Эмпирической функцией распределения называют функцию F*(x), определяющую для каждого значения х относительную частоту события Х< х. По определению F*(x) = Эмпирическая функция распределения выборки служит для оценки теоритической функции распределения генеральной совокупности. Основные свойства функции распределения выборки. 1. Эмпирическая функция распределения принимает значения из интервала 2. Функция распределения выборки является неубывающей, непрерывной слева функцией. 3. Если
Равномерное распределение. Плотность, функция распределения, математическое ожидание и дисперсия.
Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение. Исходя из основного свойства плотности вероятности, f(x) = 1/(b-a) на интервале (a;b). Основное свойство плотности вероятности: несобственный интеграл от плотности вероятности в пределах от -∞ до +∞ равен единице. Геометрически это выражается тем, что площадь фигуры, ограниченной сверху графиком плотности вероятности, снизу - осью OX, равна 1.
Математическое ожидание равномерного распределения: Пусть случайная величина
Математическое ожидание
Дисперсия равна Среднее квадратичное отклонение равномерного распределения:
|
|||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 6148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.103.12 (0.011 с.) |


 - координата точки, брошенной наудачу на отрезок
- координата точки, брошенной наудачу на отрезок  . Тогда математическое ожидание
. Тогда математическое ожидание
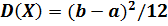
 . Вычислим второй момент:
. Вычислим второй момент:
 .
.
 и их вероятностей
и их вероятностей  . Обычно закон распределения задают в виде таблицы с двойным входом.
. Обычно закон распределения задают в виде таблицы с двойным входом. » и «строки
» и «строки  », указана вероятность
», указана вероятность 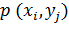 того, что двумерная СВ примет значение
того, что двумерная СВ примет значение  .
. образуют полную группу, то сумма вероятностей, помещенных во всех клетках таблицы равна 1.
образуют полную группу, то сумма вероятностей, помещенных во всех клетках таблицы равна 1. ,
,  , …,
, …,  несовместны, поэтому вероятность
несовместны, поэтому вероятность 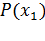 того, что Х примет значение
того, что Х примет значение  , по теореме сложения такова:
, по теореме сложения такова: .
. , надо просуммировать вероятность столбца
, надо просуммировать вероятность столбца 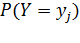 .
. 41. Функция распределения двумерной СВ, ее свойства. Вероятность попадания случайной точки в полуполосу и прямоугольник.
41. Функция распределения двумерной СВ, ее свойства. Вероятность попадания случайной точки в полуполосу и прямоугольник.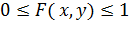


 3)
3) 
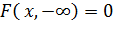 4)
4) 


 и Y < y (рисунок 2а) или в полуполосу
и Y < y (рисунок 2а) или в полуполосу  и
и  (рисунок 2б).
(рисунок 2б).
 вероятность попадания точки в квадрант с вершиной
вероятность попадания точки в квадрант с вершиной  (рисунок 2а), получим
(рисунок 2а), получим 
 .
. Таким образом, вероятность попадания случайной точки в полуполосу равна приращению функции распределения по одному из аргументов.
Таким образом, вероятность попадания случайной точки в полуполосу равна приращению функции распределения по одному из аргументов. со сторонами параллельными осям (рисунок 3). Пусть уравнения сторон таковы:
со сторонами параллельными осям (рисунок 3). Пусть уравнения сторон таковы:  .
. в этот прямоугольник. Искомую вероятность можно найти, например, так: из вероятности попадания случайной точки в полуполосу
в этот прямоугольник. Искомую вероятность можно найти, например, так: из вероятности попадания случайной точки в полуполосу  с вертикальной штриховкой (эта вероятность равна
с вертикальной штриховкой (эта вероятность равна  ) вычесть вероятность попадания точки в полуполосу
) вычесть вероятность попадания точки в полуполосу  с горизонтальной штриховкой (эта вероятность равна
с горизонтальной штриховкой (эта вероятность равна  ):
): (*)
(*) объёма
объёма  из генеральной совокупности
из генеральной совокупности  , упорядоченная в порядке неубывания элементов, т.е.
, упорядоченная в порядке неубывания элементов, т.е.  , называется вариационным рядом:
, называется вариационным рядом:
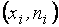 или
или  соответственно и соединяют эти точки отрезками прямых. Полученная ломаная и называется полигоном частот (если по оси ординат отложены частоты вариант) или полигоном относительных частот (если по оси ординат отложены относительные частоты вариант). Полигон можно построить и для сгруппированной выборки. Но чаще для отображения таких выборок используют гистограммы. Гистограмма – это столбчатая диаграмма, изображенная на координатной плоскости. Если отложить по оси абсцисс границы интервалов одинаковой ширины, на которые разбита сгруппированная выборка, а по оси ординат – частоты или относительные частоты соответствующих интервалов, то можно построить график в виде прямоугольников, ширина которых равна длине интервала, а высота – соответствующей частоте или относительной частоте. Полученная диаграмма называется гистограммой частот или гистограммой относительных частот соответственно. На гистограмме частот сумма всех высот равна
соответственно и соединяют эти точки отрезками прямых. Полученная ломаная и называется полигоном частот (если по оси ординат отложены частоты вариант) или полигоном относительных частот (если по оси ординат отложены относительные частоты вариант). Полигон можно построить и для сгруппированной выборки. Но чаще для отображения таких выборок используют гистограммы. Гистограмма – это столбчатая диаграмма, изображенная на координатной плоскости. Если отложить по оси абсцисс границы интервалов одинаковой ширины, на которые разбита сгруппированная выборка, а по оси ординат – частоты или относительные частоты соответствующих интервалов, то можно построить график в виде прямоугольников, ширина которых равна длине интервала, а высота – соответствующей частоте или относительной частоте. Полученная диаграмма называется гистограммой частот или гистограммой относительных частот соответственно. На гистограмме частот сумма всех высот равна  , а на гистограмме относительных частот – единице. Необходимо подчеркнуть, что гистограммы частот и относительных частот имеют смысл только в том случае, если все интервалы одинаковой ширины.
, а на гистограмме относительных частот – единице. Необходимо подчеркнуть, что гистограммы частот и относительных частот имеют смысл только в том случае, если все интервалы одинаковой ширины.


 (
(  ).
).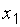 – наименьшее опытное значение, то для
– наименьшее опытное значение, то для  . Если
. Если  – наибольшая варианта, то для
– наибольшая варианта, то для  .
.



