
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центральная предельная теорема (цпт), следствия из нее.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нормальное распределение -наиболее распространенное в природе распределение непрерывных величин. Математическим обоснованием этого факта служит центральная предельная теорема: Сумма большого числа как угодно распределенных независимых случайных величин распределена асимптотически нормально, если только слагаемые вносят равномерно малый вклад в сумму. Это значит, что чем больше независимых слагаемых в сумме, тем ближе закон ее распределения к нормальному. Вместо суммы часто рассматривают среднее арифметическое большого числа случайных величин, оно отличается от суммы только множителем (1/n), поэтому его распределение также стремится к нормальному с ростом числа n суммируемых величин. Поскольку случайные величины, с которыми мы сталкиваемся, например, при измерениях, есть результат действия множества независимых факторов, понятно, почему измеряемые значения, как правило, распределены нормально. Если независимые случайные величины не распределены по нормальному закону, то можно наложить на них некоторые весьма нежесткие ограничения, и их сумма будет все-таки распределена нормально. Эту задачу поставили и решили в основном русские ученые П. Л. Чебышев и его ученики А. А. Марков и А. М. Ляпунов. Теорема (Ляпунов). Если независимые случайные величины где Фактически мы приводим не теорему Ляпунова, а одно из следствий из нее, так как этого следствия вполне достаточно для практических приложений. Поэтому условие
Смысл условия Следствием центральной предельной теоремы является широко применяемая при решении задач теорема Муавра-Лапласа: Если производится серия n независимых испытаний, в каждом из которых некоторое событие происходит с вероятностью р, то закон распределения величины,
где m - число появлений события в n испытаниях, а q = 1 - p, стремится к нормальному с матожиданием 0 и дисперсией 1 при n, стремящемся к бесконечности. Поскольку плотность нормального распределения с матожиданием 0 и дисперсией 1 как функция х, а также значение интеграла от этой плотности в пределах от 0 до z как функция z табулированы во всех учебниках и задачниках по теории вероятностей, то легко найти вероятность попадания х, а следовательно и m при известных n, p в любой интервал. Двумерная СВ. Задание закона распределения указанной СВ. Кроме одномерных случайных величин изучают величины, возможные значения которых определяются двумя, тремя,…, n числами. Такие величины называются соответственно друмерными, трехмерными,…, n – мерными. Будем обозначать через (X, Y) двумерную случайную величину. Каждую из величин X, Y называют составляющей (компонентой); обе величины X и Y, рассматриваемые одновременно, образуют систему двух СВ. Законом распределения дискретной двумерной СВ называют перечень возможных значений этой величины, т.е. пар чисел Первая строка таблицы содержит все возможные значения составляющей Х, а первый столбец – все возможные значения составляющей Y. В клетке, стоящей на пересечении «столбца Так как события Зная закон распределения двумерной дискретной СВ, можно найти законы распределения каждой из составляющих. Действительно, например события
Функцией распределения двумерной СВ (X, Y) называют функцию F(x,y), определяющую для каждой пары чисел х, у вероятность того, что Х примет значение, меньшее х, и при этом Y примет значение, меньшее у: F(x, y) = P(X< x, Y< y). Свойство 1. Значение функции распределения удовлетворяют двойному неравенству Свойство 2. F(x, y) есть неубывающая функция по каждому аргументу т.е.
Свойство 3. Имеют место предельные соотношения: 1) 2) Свойство 4. a) При y = ∞ функция распределения системы становится функцией распределения составляющей X:
Используя функция распределения системы СВ X и Y, легко найти вероятность того, что в результате испытания случайная точка попадает в полуполосу
Вычитая из вероятности попадания случайной точки в квадрант с вершиной Аналогично имеем
Рассмотрим прямоугольник
Найдем вероятность попадания случайной точки
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1062; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.008 с.) |

 имеют конечные математические ожидания
имеют конечные математические ожидания  и конечные дисперсии
и конечные дисперсии  , число их достаточно велико, а при неограниченном возрастании
, число их достаточно велико, а при неограниченном возрастании 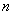
 ,
, - абсолютные центральные моменты третьего порядка, то сумма их с достаточной степенью точности имеет распределение
- абсолютные центральные моменты третьего порядка, то сумма их с достаточной степенью точности имеет распределение 

 и их вероятностей
и их вероятностей  . Обычно закон распределения задают в виде таблицы с двойным входом.
. Обычно закон распределения задают в виде таблицы с двойным входом. » и «строки
» и «строки  », указана вероятность
», указана вероятность 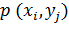 того, что двумерная СВ примет значение
того, что двумерная СВ примет значение  .
. образуют полную группу, то сумма вероятностей, помещенных во всех клетках таблицы равна 1.
образуют полную группу, то сумма вероятностей, помещенных во всех клетках таблицы равна 1. ,
,  , …,
, …,  несовместны, поэтому вероятность
несовместны, поэтому вероятность 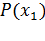 того, что Х примет значение
того, что Х примет значение  , по теореме сложения такова:
, по теореме сложения такова: .
. , надо просуммировать вероятность столбца
, надо просуммировать вероятность столбца 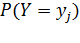 .
. 41. Функция распределения двумерной СВ, ее свойства. Вероятность попадания случайной точки в полуполосу и прямоугольник.
41. Функция распределения двумерной СВ, ее свойства. Вероятность попадания случайной точки в полуполосу и прямоугольник.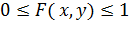


 3)
3) 
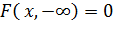 4)
4) 


 и Y < y (рисунок 2а) или в полуполосу
и Y < y (рисунок 2а) или в полуполосу  и
и  (рисунок 2б).
(рисунок 2б).
 вероятность попадания точки в квадрант с вершиной
вероятность попадания точки в квадрант с вершиной  (рисунок 2а), получим
(рисунок 2а), получим 
 .
. Таким образом, вероятность попадания случайной точки в полуполосу равна приращению функции распределения по одному из аргументов.
Таким образом, вероятность попадания случайной точки в полуполосу равна приращению функции распределения по одному из аргументов. со сторонами параллельными осям (рисунок 3). Пусть уравнения сторон таковы:
со сторонами параллельными осям (рисунок 3). Пусть уравнения сторон таковы:  .
. в этот прямоугольник. Искомую вероятность можно найти, например, так: из вероятности попадания случайной точки в полуполосу
в этот прямоугольник. Искомую вероятность можно найти, например, так: из вероятности попадания случайной точки в полуполосу  с вертикальной штриховкой (эта вероятность равна
с вертикальной штриховкой (эта вероятность равна  ) вычесть вероятность попадания точки в полуполосу
) вычесть вероятность попадания точки в полуполосу  с горизонтальной штриховкой (эта вероятность равна
с горизонтальной штриховкой (эта вероятность равна  ):
): (*)
(*)


