
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предельные теоремы теории вероятностей.Содержание книги
Поиск на нашем сайте В конце 19 века в теории вероятностей возникло направление исследований, которое получило название: предельные теоремы теории вероятностей. В этом направлении, начало которого было положено нашими соотечественниками П.Л.Чебышевым, А.А.Марковым, А.М.Ляпуновым, по сей день ведутся интенсивные исследования. Предельные теоремы теории вероятностей можно разбить на две большие группы. 1. Одна группа теорем составляет "закон больших чисел". Закон больших чисел формулирует условия, при которых совокупное действие большого числа случайных факторов приводит к результату почти не зависящему от случая (т.е. практически постоянный результат) 2. Вторая группа теорем связана с выяснением вопроса о распределении сумм большого числа случайных величин. В этих теоремах выясняется, какие законы распределения может иметь сумма случайных величин, если число слагаемых неограниченно увеличивается, и какие условия при этом нужно наложить на сами величины. В частности, центральная предельная теорема посвящена установлению сумм, при которых возникает нормальный закон распределения. Центральная предельная теорема Первый вариант этой теоремы был доказан в 1912 г. А.М.Ляпуновым. В настоящее время имеется несколько формулировок этой теоремы, различающихся условиями, которые накладываются на случайные величины. Мы приведём простейший вариант центральной предельной теоремы для одинаково распределённых независимых случайных величин. Пусть ТЕОРЕМА. Если случайные величины Так как в условиях теоремы случайные величины независимы, то т.е. в условиях теоремы сумма Мы не приводим доказательства теоремы потому, что оно требует введения многих дополнительных понятий и утверждений. Было потрачено немало усилий, чтобы ослабить условия, налагаемые на случайные величины в центральной предельной теореме. В частности, оказалось, что утверждение теоремы остаётся в силе и для слабо зависимых случайных величин. Как уже отмечалось, существует много вариантов и соответственно формулировок центральной предельной теоремы, но во всех этих вариантах суть условий одна: Если случайная величина может быть представлена в виде суммы большого числа независимых (или слабо зависимых) случайных величин, каждая из которых мала по сравнению с суммой, то эта сумма имеет закон распределения близкий к нормальному. Пример 1. Наглядной иллюстрацией действия центральной предельной теоремы является рассеивание снарядов при артиллерийской стрельбе. На траекторию снаряда действует большое количество независимых факторов, влияние каждого из которых невелико. Этими факторами являются отклонения в размере заряда, в размере и весе снаряда, сила и направление ветра на разных высотах, плотность воздушных вихрей, зависящая от температуры и влажности воздуха, и т.д. В результате отклонение снаряда от цели имеет приблизительно нормальный закон распределения. Пример 2. Другими широко известным примером может служить ошибка возникшая при измерениях. Ошибка, как правило, является суммой малых ошибок возникающих из-за действия случайных факторов таких, как температура окружающей среды, состояние наблюдателя, состояние измерительного прибора и т.д.
Классическая Ц. П. Т Пусть
Тогда
где
Скорость сходимости можно оценить с помощью неравенства Берри — Эссеена. Замечания Неформально говоря, классическая центральная предельная теорема утверждает, что сумма
билет №_12_
|
||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 859; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |

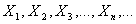 последовательность одинаково распределённых случайных величин с математическими ожиданиями
последовательность одинаково распределённых случайных величин с математическими ожиданиями  и дисперсиями
и дисперсиями 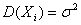 .
.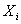 независимы и
независимы и  , то при достаточно большом n закон распределения суммы
, то при достаточно большом n закон распределения суммы 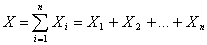 будет сколь угодно близок к нормальному закону распределения
будет сколь угодно близок к нормальному закону распределения 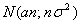 .
.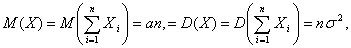
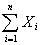 имеет закон распределения близкий к
имеет закон распределения близкий к  с ростом п, возрастают, то удобнее рассматривать не просто суммы
с ростом п, возрастают, то удобнее рассматривать не просто суммы 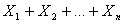 , а нормированные суммы
, а нормированные суммы 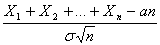 . Такие суммы при
. Такие суммы при 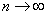 имеют закон распределения
имеют закон распределения 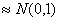 .
. есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию. Обозначим последние
есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию. Обозначим последние 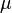 и
и 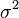 , соответственно. Пусть также
, соответственно. Пусть также .
.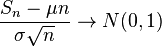 по распределению при
по распределению при 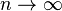 ,
,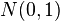 — нормальное распределение с нулевым математическим ожиданием и стандартным отклонением, равным единице. Обозначив символом
— нормальное распределение с нулевым математическим ожиданием и стандартным отклонением, равным единице. Обозначив символом  выборочное среднее первых
выборочное среднее первых  величин, то есть
величин, то есть 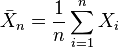 , мы можем переписать результат центральной предельной теоремы в следующем виде:
, мы можем переписать результат центральной предельной теоремы в следующем виде: по распределению при
по распределению при 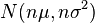 . Эквивалентно,
. Эквивалентно,  .
.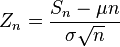 , получаем
, получаем  , где
, где  — функция распределения стандартного нормального распределения.
— функция распределения стандартного нормального распределения.


