
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределения непрерывных случайных величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Равномерное распределение. Непрерывная величина Х распределена равномерно на интервале (a, b), если все ее возможные значения находятся на этом интервале и плотность распределения вероятностей постоянна:
Примерами равномерно распределенных величин являются ошибки округления. Так, если все табличные значения некоторой функции округлены до одного и того же разряда Показательное распределение. Непрерывная случайная величина Х имеет показательное распределение, если плотность распределения ее вероятностей выражается формулой:
График плотности распределения вероятностей (31) представлен на рис. 5.
Время Т безотказной работы компьютерной системы есть случайная величина, имеющая показательное распределение с параметром λ, физический смысл которого – среднее число отказов в единицу времени, не считая простоев системы для ремонта. Нормальное (гауссово) распределение. Случайная величина Х имеет нормальное (гауссово) распределение, если плотность распределения ее вероятностей определяется зависимостью:
где m = M (X), При График плотности нормального распределения (32) представлен на рис. 6.
Нормальное распределение является наиболее часто встречающимся в различных случайных явлениях природы. Так, ошибки выполнения команд автоматизированным устройством, ошибки вывода космического корабля в заданную точку пространства, ошибки параметров компьютерных систем и т.д. в большинстве случаев имеют нормальное или близкое к нормальному распределение. Более того, случайные величины, образованные суммированием большого количества случайных слагаемых, распределены практически по нормальному закону.
Гамма-распределение. Случайная величина Х имеет гамма-распределение, если плотность распределения ее вероятностей выражается формулой:
где Основные свойства гамма-функции:
Параметры
билет №_10_ Накопители на жестких магнитных дисках. Устройство, технические характеристики, физический и логический уровни хранения информации (дорожка, сектор, цилиндр, кластер, файл). Точечные оценки параметров. Случайные и систематические ошибки. Оценочные функции. Характеристики качества оценок: смещенность, эффективность, робастность. Оценки математического ожидания и дисперсии. Точечные оценки параметров. Случайные и систематические ошибки. Оценочные функции. Характеристики качества оценок: смещенность, эффективность, робастность. Оценки математического ожидания и дисперсии. Точечные оценки. Точечной оценкой наз. такая Оценка (О), значение к-рой представимо геометрически в виде точки в том же пространстве, что и значения неизвестных параметров (размерность пространства равна числу оцениваемых параметров). Именно точечные О. с. и используются как приближенные значения для неизвестных физич. величин. В дальнейшем для простоты предполагается, что оценке подлежит один единственный параметр; в этом случае точечная О. с. представляет собой функцию от результатов наблюдений, принимающую числовые значения. Точечные оценки могут быть состоятельными, несмещенными и эффективными. Состоятельной называется оценка, которая при увеличении объема выборки стремится по вероятности к истинному значению числовой характеристики. Несмещенной называется оценка, математическое ожидание которой равно оцениваемой числовой характеристике (параметру). Оценка называется эффективной, если ее дисперсия меньше дисперсии любой другой оценки данного параметра, т.е. наиболее эффективной считают ту из нескольких возможных несмещенных оценок, которая имеет наименьшую дисперсию.
Требование несмещенности на практике не всегда целесообразно, так как оценка с небольшим смещением и малой дисперсией может оказаться предпочтительнее несмещенной оценки с большой дисперсией. На практике не всегда удается удовлетворить одновременно все три этих требования, однако выбору оценки должен предшествовать ее критический анализ со всех перечисленных точек зрения. Наиболее распространенным методом получения оценок является, метод наибольшего (максимального) правдоподобия, теоретически обоснованный математиком Р. Фишером, который приводит к асимптотически несмещенным и эффективным оценкам с приближенно нормальным распределением. Среди других методов можно назвать методы моментов и наименьших квадратов.
|
||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 644; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.86.112 (0.01 с.) |

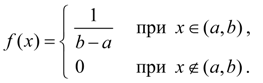 (29)
(29) (30)
(30)
 , то выбирая наугад табличное значение, мы считаем, что ошибка округления выбранного числа есть случайная величина, равномерно распределенная в интервале
, то выбирая наугад табличное значение, мы считаем, что ошибка округления выбранного числа есть случайная величина, равномерно распределенная в интервале 
 (31)
(31)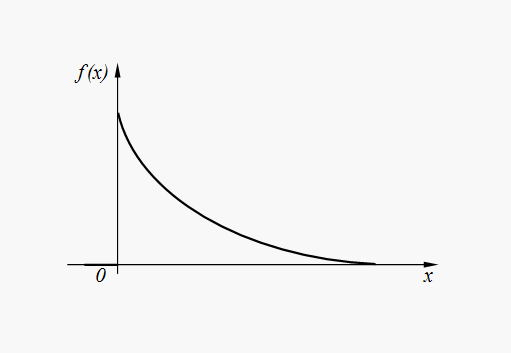
 (32)
(32) .
. нормальное распределение называется стандартным.
нормальное распределение называется стандартным.
 (33)
(33) – гамма-функция Эйлера.
– гамма-функция Эйлера.
 – любые положительные числа. Гамма-распределение является также распределением Пирсона типа III [3]. При
– любые положительные числа. Гамма-распределение является также распределением Пирсона типа III [3]. При  гамма-распределение превращается в показательное распределение с параметром λ, так как Г(1) = 1. Гамма-распределение широко используется в математической статистике. Hа рис. 7 представлены графики плотности гамма-распределения (33) при
гамма-распределение превращается в показательное распределение с параметром λ, так как Г(1) = 1. Гамма-распределение широко используется в математической статистике. Hа рис. 7 представлены графики плотности гамма-распределения (33) при  .
.



