
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция распределения системы двух случайных величин и ее свойства. ( в файле 2)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Функцией распределения вероятностей системы двух случайных величин называется функция двух аргументов
Геометрически функцию распределения системы двух случайных величин можно интерпретировать как вероятность попадания случайной точки
Сформулируем основные свойства функции распределения вероятностей системы двух случайных величин.
Свойство 1.
или символически
Свойство 2.
Свойство 3.
или
Свойство 4. Функция распределения является неубывающей функцией по каждому аргументу:
Свойство 5. Вероятность попадания случайной точки
Плотность распределения системы случайных величин и ее свойства. (в файле 2) Предположим, что функция распределения
Функция
Используя формулу (5.1), выразим функцию распределения системы
Рассмотрим свойства плотности распределения системы двух случайных величин.
Свойство 1. Плотность распределения есть функция неотрицательная:
Свойство 2. Двойной несобственный интеграл с бесконечными пределами от плотности распределения системы равен единице:
Плотности распределения СВ, входящих в систему, условный закон распределения. (в файле 2) Условные законы распределения
Пусть известна плотность распределения системы двух случайных величин. Используя свойства функций распределения, можно вывести формулы для нахождения плотности распределения одной величины, входящей в систему:
Перейдем теперь к решению обратной задачи: по известным законам распределения отдельных величин, входящих в систему, найти закон распределения системы. Легко увидеть, что в общем случае эта задача неразрешима. Действительно, с одной стороны, законы распределения отдельных случайных величин, входящих в систему, характеризуют каждую из случайных величин в отдельности, но ничего не говорят о том, как они взаимосвязаны. С другой стороны, искомый закон распределения системы должен содержать все сведения о случайных величинах системы, в том числе и о характере связей между ними.
Таким образом, если случайные величины
Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина, входящая в систему, приняла определенное значение, называется условным законом распределения.
Условный закон распределения можно задавать как функцией распределения, так и плотностью распределения. Условная функция распределения обозначается
Плотностью распределения для случайной величины
Аналогично плотностью распределения для случайной величины
Условная плотность распределения обладает всеми свойствами безусловной плотности распределения. В частности,
24. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции. 25. Центральным моментом порядка s, h системы СВ (X, Y) называется математическое ожидание произведения степеней s, h соответствующих центрированных случайных величин:
Вторые центральные моменты: Коэффициент корреляции служит мерой линейной зависимости между случайными величинами.
25. Неравенство Чебышева. Нера́венство Чебышёва в теории вероятностей утверждает, что случайная величина в основном принимает значения близкие к своему среднему. Более точно, оно даёт оценку вероятности, что случайная величина примет значение далёкое от своего среднего. Неравенство Чебышёва является следствием неравенства Маркова. Формулировки Пусть случайная величина
Если
|
|||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 875; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.1.58 (0.006 с.) |

 , равная вероятности совместного выполнения двух неравенств
, равная вероятности совместного выполнения двух неравенств  и
и  , т. е.
, т. е.
 в левый нижний бесконечный квадрант плоскости (рис. 14) с вершиной в точке
в левый нижний бесконечный квадрант плоскости (рис. 14) с вершиной в точке  .
.

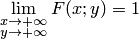 или
или 



 непрерывна и дважды дифференцируема. Тогда смешанная частная производная функции
непрерывна и дважды дифференцируема. Тогда смешанная частная производная функции 
 называется плотностью распределения системы непрерывных случайных величин
называется плотностью распределения системы непрерывных случайных величин 


 .
.
 взаимозависимы, то закон распределения системы не может быть выражен через законы распределения отдельных случайных величин, входящих в систему. Это приводит к необходимости введения условных законов распределения.
взаимозависимы, то закон распределения системы не может быть выражен через законы распределения отдельных случайных величин, входящих в систему. Это приводит к необходимости введения условных законов распределения. , условная плотность распределения —
, условная плотность распределения —  (мы записали условные законы распределения случайной величины
(мы записали условные законы распределения случайной величины  при условии, что другая случайная величина
при условии, что другая случайная величина  приняла определенное значение).
приняла определенное значение).
 . Отсюда получаем
. Отсюда получаем  .
.


 :
:

 - характеризует рассеяние случайных величин в направлении оси OX.
- характеризует рассеяние случайных величин в направлении оси OX. - характеризует рассеяние случайных величин в направлении оси OY.
- характеризует рассеяние случайных величин в направлении оси OY.
 , отсюда
, отсюда 
 где
где 

 , то случайные величины линейно зависимы;
, то случайные величины линейно зависимы; , то случайные величины не коррелированны, что не означает их независимости вообще.
, то случайные величины не коррелированны, что не означает их независимости вообще. определена на вероятностном пространстве
определена на вероятностном пространстве  , и её математическое ожидание
, и её математическое ожидание  и дисперсия
и дисперсия  конечны. Тогда
конечны. Тогда , где
, где  .
. , где
, где  - стандартное отклонение и
- стандартное отклонение и  , то получаем
, то получаем В частности, случайная величина с конечной дисперсией отклоняется от среднего больше, чем на
В частности, случайная величина с конечной дисперсией отклоняется от среднего больше, чем на  стандартных отклонения с вероятностью меньше
стандартных отклонения с вероятностью меньше  . Она отклоняется от среднего на
. Она отклоняется от среднего на  стандартных отклонения с вероятностью меньше
стандартных отклонения с вероятностью меньше  .
.


