
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мода и медиана случайной величиныСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Модой дискретной случайной величины называется наиболее вероятное значение. Для непрерывной случайной величины мода есть такое значение случайной величины, которому отвечает наибольшее значение плотности распределения.
Моменты случайной величины. Момент случайной величины — числовая характеристика распределения данной случайной величины. Если дана случайная величина
если математическое ожидание
если математическое ожидание в правой части этого равенства определено. Замечания Если определены моменты В силу линейности математического ожидания центральные моменты могут быть выражены через начальные, и наоборот. Например:
Геометрический смысл некоторых моментов
называется коэффициентом асимметрии.
называется коэффициентом эксцесса распределения Вычисление моментов Моменты могут быть вычислены напрямую через определение путём интегрирования соответствующих степеней случайной величины. В частности, для абсолютно непрерывного распределения с плотностью
если а для дискретного распределения с функцией вероятности
если Также моменты случайной величины могут быть вычислены через ее характеристическую функцию
Если распределение таково, что для него в некоторой окрестности нуля определена производящая функция моментов
Коэффициент ассиметрии, эксцесс. Коэффициент асимметрии: Числовая характеристика асимметрии распределения вероятностей, определяемая через центральные моменты 2-го и 3-го порядков: Коэффицие́нт асимметри́и (skewness) — числовая характеризующая степени несимметричности распределения данной случайной величины. Пусть задана случайная величина Коэффициент асимметрии распределения случайной величины
ЭКСЦЕССА КОЭФФИЦИЕНТ , эксцесс,- скалярная характеристика островершинности графика плотности вероятности унимодального распределения, к-рую используют в качестве нек-рой меры отклонения рассматриваемого распределения от нормального. Э. к.
Биномиальное распределение. Биномиальное распределение распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях. Если при каждом испытании вероятность появления события равна р, причём 0 ≤ p ≤ 1, то число μ появлений этого события при n независимых испытаниях есть случайная величина, принимающая значения m = 1, 2,.., n с вероятностями
где q = 1 — p, a Распределение Пуассона. Распределение Пуассона — вероятностное распределение дискретного типа, моделируетслучайную величину Распределение Пуассона играет ключевую роль в теории массового обслуживания. Выберем фиксированное число
где · · Тот факт, что случайная величина
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1411; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.57.41 (0.01 с.) |

 .
. определённая на некотором вероятностном пространстве, то:
определённая на некотором вероятностном пространстве, то: -м начальным моментом случайной величины
-м начальным моментом случайной величины  называется величина
называется величина
 в правой части этого равенства определено;
в правой части этого равенства определено; называется величина
называется величина





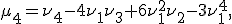 и т. д.
и т. д. равняется математическому ожиданию случайной величины и показывает относительное расположение распределения на числовой прямой.
равняется математическому ожиданию случайной величины и показывает относительное расположение распределения на числовой прямой. равняется дисперсии распределения
равняется дисперсии распределения  и показывает разброс распределения вокруг среднего значения.
и показывает разброс распределения вокруг среднего значения. , будучи соответствующим образом нормализован, является числовой характеристикой симметрии распределения. Более точно, выражение
, будучи соответствующим образом нормализован, является числовой характеристикой симметрии распределения. Более точно, выражение
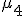 контролирует, насколько ярко выражена вершина распределения в окрестности среднего. Величина
контролирует, насколько ярко выражена вершина распределения в окрестности среднего. Величина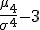

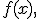 имеем:
имеем:



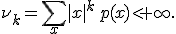
 :
:
 то моменты могут быть вычислены по следующей формуле:
то моменты могут быть вычислены по следующей формуле:

 , такая что
, такая что  .
.
 определяется по формуле
определяется по формуле
 есть 2-й коэффициент Пирсона,
есть 2-й коэффициент Пирсона,  и
и  - 2-й и 4-й центральные моменты вероятностного распределения.
- 2-й и 4-й центральные моменты вероятностного распределения.
 — биномиальные коэффициенты (отсюда название Б. р.). Приведённая формула иногда называется формулой Бернулли. Математическое ожидание и Дисперсия величины μ, имеющей Б. р., равны М (μ) = np и D (μ) = npq, соответственно. При больших n, в силу Лапласа теоремы (См. Лапласа теорема), Б. р. близко к нормальному распределению (См. Нормальное распределение), чем и пользуются на практике. При небольших n приходится пользоваться таблицами Б. р.
— биномиальные коэффициенты (отсюда название Б. р.). Приведённая формула иногда называется формулой Бернулли. Математическое ожидание и Дисперсия величины μ, имеющей Б. р., равны М (μ) = np и D (μ) = npq, соответственно. При больших n, в силу Лапласа теоремы (См. Лапласа теорема), Б. р. близко к нормальному распределению (См. Нормальное распределение), чем и пользуются на практике. При небольших n приходится пользоваться таблицами Б. р. и определим дискретное распределение, задаваемое следующей функцией вероятности:
и определим дискретное распределение, задаваемое следующей функцией вероятности: ,
, обозначает факториал числа
обозначает факториал числа 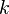 ,
, — основание натурального логарифма.
— основание натурального логарифма.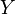 имеет распределение Пуассона с параметром
имеет распределение Пуассона с параметром  , записывается:
, записывается:  .
.


