
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисперсия случайной величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Дисперсия случайной величины есть характеристика распределения, разбросанность значений случайной величины около ее математического ожидания. Само слово дисперсия означает ”рассеивание”. Дисперсия случайной величины – это математическое ожидание квадрата отклонения случайной величины от ее математического ожидания
Если
То Когда
Поэтому вводится еще одна мера рассеивания с размерностью, совпадающей с размерностью случайной величины. Это так называемое среднее квадратичное отклонение, которое определяется как корень квадратный из дисперсии. Среднее квадратичное отклонение обозначается символом: Свойства дисперсии Свойства дисперсии: 1. Дисперсия постоянной величины всегда равна нулю. Действительно,
2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат. Действительно, 3. Дисперсия алгебраической суммы двух независимых случайных величин равна сумме их дисперсий, то есть 4. Упрощенное правило вычисления дисперсии: дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания, то есть Доказательство ведь
Система случайных величин. Свойства распределения двумерного случайного вектора В ТВ часто приходится сталкиваться с задачами, в которых результат опыта описывается не одной случайной величиной, а двумя или более СВ, образующими комплекс или систему. Например, точка попадания снаряда определяется не одной случайной величиной, а двумя: абсциссой и ординатой – и может быть рассмотрена как комплекс двух случайных величин. Пусть имеется упорядоченная система n случайных величин Тогда Чтобы задать случайный вектор, надо указать все те значения, которые он может принимать, и соответствующие этим значениям вероятности, т.е. вероятности, с которыми эти значения принимаются. Универсальным способом задания случайного вектора является задание его функции распределения, которая определяется равенством
В двумерном случае Y
y M(x,y)
0 x X
Остановимся подробнее на двумерном случае. При этом пусть 1. по каждой из переменных; 3. 4.
Функция распределения дискретного двумерного случайного вектора. Пусть распределение вектора
Здесь Функциия распределения вектора
где суммирование распространяется на все
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 478; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.22.34 (0.007 с.) |

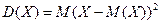 .
. - дискретная случайная величина, которая задается как
- дискретная случайная величина, которая задается как
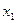








 , то
, то . Дисперсия как мера рассеивания значений случайной величины обладает тем недостатком, что ее размерность не совпадает с размерностью случайной величины (размерность дисперсии – это квадрат размерности случайной величины).
. Дисперсия как мера рассеивания значений случайной величины обладает тем недостатком, что ее размерность не совпадает с размерностью случайной величины (размерность дисперсии – это квадрат размерности случайной величины). или
или  ,
, 
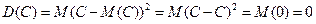 .
.

 Здесь было использовано свойство математического ожидания: если
Здесь было использовано свойство математического ожидания: если  и
и  – независимые случайные величины, то
– независимые случайные величины, то  .
. .
.
 - постоянная величина.
- постоянная величина. . Будем называть ее случайной векторной или
. Будем называть ее случайной векторной или  -мерной случайной величиной и обозначать так:
-мерной случайной величиной и обозначать так: 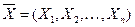 .
. -ая случайная координата вектора
-ая случайная координата вектора 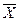 . Упорядоченную систему из
. Упорядоченную систему из  .
. - это вероятность попадания случайной точки
- это вероятность попадания случайной точки  в область
в область










 ,
,  . Свойства функции распределения случайного вектора аналогичны свойствам функции распределения случайной величины. Перечислим их:
. Свойства функции распределения случайного вектора аналогичны свойствам функции распределения случайной величины. Перечислим их: ; 2.
; 2.  - неубывающая функция
- неубывающая функция ,
, 



 - дискретное, и
- дискретное, и  , а
, а  . Тогда все возможные ситуации отражаются в таблице:
. Тогда все возможные ситуации отражаются в таблице: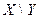



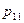






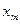

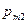

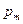


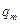
 – это вероятность того, что случайный вектор
– это вероятность того, что случайный вектор 


 - вероятность того, что
- вероятность того, что  независимо от значений случайной величины
независимо от значений случайной величины  - вероятность того, что
- вероятность того, что  независимо от значений случайной величины
независимо от значений случайной величины 
 , для которых
, для которых  , а
, а  принимает все такие значения, для которых
принимает все такие значения, для которых  .
.


