
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики случайной точкиСодержание книги
Поиск на нашем сайте Случайную точку характеризуют пять чисел:
где Пример. В урне три шара с номерами 1, 2, 3. Вынимают наугад два шара. Х – номер первого шара, Y – номер второго шара. Закон распределения случайной точки (Х,Y) был составлен в п.2.5.2:
1. Вероятности значений случайной величины Х вычисляются суммированием по строкам, случайной величины Y – суммированием по столбцам. Таким образом, законы распределения случайных величин Х и Y имеют вид:
Из этого примера видно, что по совместному распределению двух случайных величин можно восстановить закон распределения каждой из них в отдельности. Обратное неверно. 2. Числовые характеристики случайных величин Х и Y: 1) математическое ожидание:
аналогично 2) дисперсия:
аналогично, 3) среднее квадратическое отклонение:
3. Числовые характеристики случайной точки (Х,Y) находим по формуле
По формуле (2.14) находим
Линейная регрессия Пусть (Х,Y) – двумерная случайная величина, где Х и Y – зависимые случайные величины. Возможно приближенное представление величины Y в виде линейной функции величины Х:
где Функция (2.15) называется наилучшим приближением в смысле метода наименьших квадратов, если математическое ожидание Теорема. Линейная среднеквадратическая регрессияY на Х имеет вид:
где Коэффициент
реализующую линейную зависимость (2.16) случайной величины Y от случайной величины Х, называют прямой среднеквадратической регрессии Y на Х (линией регрессии Y на X). Поскольку зависимость (2.16) является приближенной, то существует погрешность этого приближения, называемая остаточной дисперсией:
Аналогичную форму записи имеет прямая среднеквадратической регрессии Х на Y (линия регрессии X на Y):
Пример. Найти линейную среднюю квадратичную регрессию и остаточную дисперсию случайной величины Y на случайную величину Х по данным примера п. 2.5.5. Решение. Для двумерной случайной величины (X,Y), приведенной в примере 2.5.5, все необходимые числовые характеристики найдены:
Из уравнения (2.16) получаем искомое соотношение:
Остаточная дисперсия рассчитывается по формуле (2.17):
Для оценки среднеквадратичной погрешности линейной регрессии обычно используют величину
Закон больших чисел Закон больших чисел – это теорема, доказательство которой основано на следующих леммах. Лемма 1. Неравенство Маркова. Пусть X – неотрицательная непрерывная случайная величина. Тогда для любого числа
Доказательство. Докажем неравенство Маркова для случая непрерывной случайной величины. Построим оценку M(X):
При построении оценки использованы определение математического ожидания непрерывной случайной величины, условие неотрицательности случайной величины Х, свойство плотности вероятности:
Из полученной оценки Пример 1. Среднее количество вызовов, поступающих в течение часа на телефонную станцию, равно 300. Оценить вероятность того, что в течение часа число вызовов: 1) превысит 400; 2) будет не более 500. Решение. Пусть Х – число вызовов, поступающих на телефонную станцию в течение часа. По условию задачи Используя неравенство Маркова, получаем:
1) 2)
Ответ:
Лемма 2. Неравенство Чебышева. Пусть Х – случайная величина с числовыми характеристиками
Доказательство. Используя неравенство Маркова и определение дисперсии, имеем:
Пример 2. Средний расход воды на перерабатывающей станции составляет 1000 л в день. Отклонение от нормы не превышает 200 л в день. Оценить вероятность того, что расход воды в день не превысит 2000 л: 1) по неравенству Маркова; 2) по неравенству Чебышева. Решение. Пусть случайная величина Х – расход воды в день (л). По условию задачи
1)
т. е. В данной задаче оценку вероятности события, найденную с помощью неравенства Маркова Будем в дальнейшем кратко называть случайные величины однотипными, если они имеют одно и то же математическое ожидание а и одну и ту же дисперсию D. Лемма 3. О среднем арифметическом. Пусть
Доказательство. Случайная величина
имеет числовые характеристики
Применяя к случайной величине Х неравенство Чебышева, получим:
что и требовалось доказать. Теорема. Закон больших чисел. Пусть Тогда для любого числа
Последнее означает, что при достаточно больших
т. е. среднее арифметическое большого числа однотипных независимых случайных факторов практически неслучайная величина. Доказательство. Всилу леммы 3 и с учетом того, что
Учитывая, что
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 416; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.01 с.) |

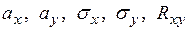 ,
, – числовые характеристики случайной величины Х;
– числовые характеристики случайной величины Х; 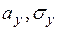 – числовые характеристики случайной величины Y;
– числовые характеристики случайной величины Y; 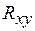 – коэффициент корреляции.
– коэффициент корреляции.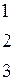
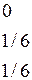
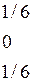

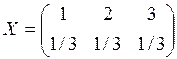 ;
; 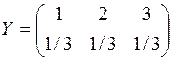 .
. ,
, ;
;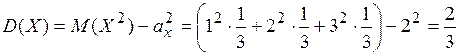 ,
,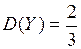 ;
;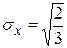 ,
,  .
. .
.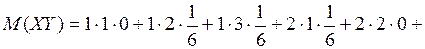
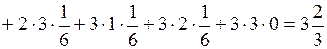 .
.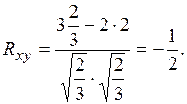
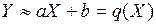 , (2.15)
, (2.15)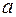 и
и 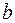 – параметры, подлежащие определению. Обычно эти параметры определяются методом наименьших квадратов.
– параметры, подлежащие определению. Обычно эти параметры определяются методом наименьших квадратов.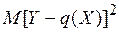 принимает наименьшее возможное значение. Функцию
принимает наименьшее возможное значение. Функцию 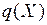 называют среднеквадратической регрессией Y на Х.
называют среднеквадратической регрессией Y на Х. , (2.16)
, (2.16)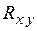 – коэффициент корреляции,
– коэффициент корреляции,  и
и 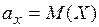 – математические ожидания величин Y и Х соответственно.
– математические ожидания величин Y и Х соответственно.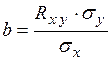 называют коэффициентом регрессии Y на Х, а прямую
называют коэффициентом регрессии Y на Х, а прямую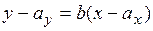 ,
,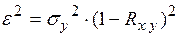 . (2.17)
. (2.17)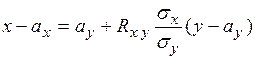 .
.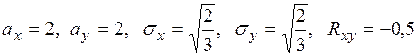 .
.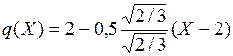 или
или .
. .
. , в нашем случае она составляет:
, в нашем случае она составляет: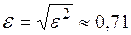 .
.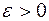 справедливо неравенство
справедливо неравенство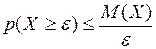 .
.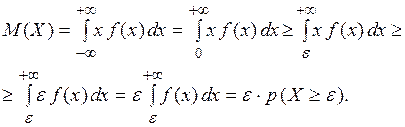
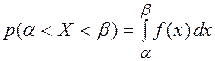 для
для 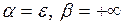 .
. после деления на
после деления на  получаем требуемое неравенство.
получаем требуемое неравенство.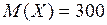 .
. ;
; .
.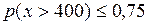 ;
; 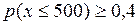 , т. е. не более чем в 75% случаев на станцию в течение часа поступит более 400 вызовов; не менее чем в 40% случаев в течение часа на станцию поступит не более 500 вызовов.
, т. е. не более чем в 75% случаев на станцию в течение часа поступит более 400 вызовов; не менее чем в 40% случаев в течение часа на станцию поступит не более 500 вызовов. и
и  . Тогда для любого числа
. Тогда для любого числа 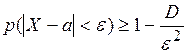 .
.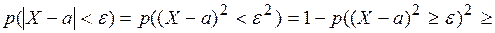
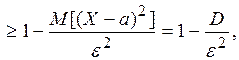 что и требовалось доказать.
что и требовалось доказать.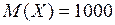 и
и 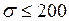 . Построим оценки:
. Построим оценки: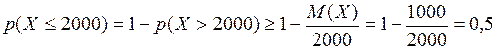 ;
;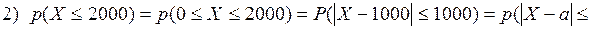
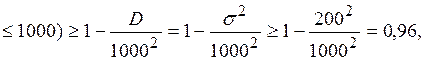
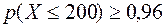 по неравенству Чебышева.
по неравенству Чебышева. , удалось уточнить с помощью неравенства Чебышева
, удалось уточнить с помощью неравенства Чебышева  .
. – независимые однотипные случайные величины с числовыми характеристиками а и D. Тогда для любого числа
– независимые однотипные случайные величины с числовыми характеристиками а и D. Тогда для любого числа 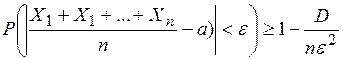 .
.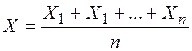
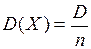 . Это следует из свойств математического ожидания и дисперсии для независимых случайных величин:
. Это следует из свойств математического ожидания и дисперсии для независимых случайных величин:
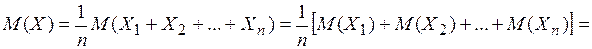
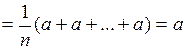 ;
;

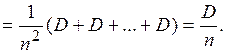
 ,
,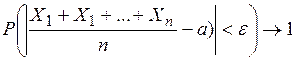 при
при 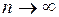 . (2.18)
. (2.18) с практической достоверностью (с вероятностью
с практической достоверностью (с вероятностью 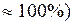
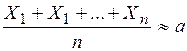 ,
,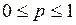 получаем двойное неравенство:
получаем двойное неравенство: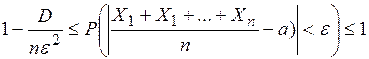 .
.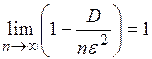 и свойство пределов «О двух милиционерах», получаем требуемое соотношение (2.18). Закон больших чисел был впервые получен русским математиком П. Л. Чебышевым.
и свойство пределов «О двух милиционерах», получаем требуемое соотношение (2.18). Закон больших чисел был впервые получен русским математиком П. Л. Чебышевым.


