
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь признаков, измеренных в номинальных шкалахСодержание книги
Поиск на нашем сайте
Ограничимся двумя признаками Х и
По частотам Понятие о многомерном анализе И других статистических методах На практике при обследовании некоторого объекта измеряется не один, а несколько его признаков. В таких опытах каждое наблюдение представляется некоторым конечным упорядоченным набором чисел. Часть математической статистики, которая исследует эксперименты с такими многомерными наблюдениями, называется многомерным статистическим анализом. Одномерный статистический анализ является частным случаем многомерного. При планировании эксперимента следует стремиться к тому, чтобы признаков было меньше, т. к. каждый признак, не несущий полезной информации (или несущий её малое количество), только создает помехи для анализа. Факторный анализ Одним из наиболее распространенных методов многомерного анализа является факторный анализ. При исследовании сложных объектов и их систем (в психологии, биологии, социологии и т. д.) часто невозможно непосредственно измерить величины, определяющие свойства этих объектов (так называемые факторы), а иногда неизвестны даже количество и смысл факторов, поэтому производят измерения величин, зависящих от последних. Для обнаружения влияющих на измеряемые переменные факторов используются методы факторного анализа. Например, изучение различных свойств личности, которые не поддаются прямому измерению, происходит с помощью психологических тестов. Затем тестовые баллы подвергаются факторному анализу, который позволяет выявить личностные свойства, оказавшие влияние на поведение испытуемых. Опишем в общих чертах схему факторного анализа. Вычисляют коэффициенты корреляции между всевозможными парами переменных и составляют из них интеркорреляционную матрицу (в ней справа и сверху цифрами обозначены изученные в эксперименте переменные, а внутри показаны их корреляции друг с другом; поскольку всевозможных пар в данном случае меньше, чем клеток матрицы, то заполняется только часть матрицы, расположенная выше её главной диагонали). Приведем пример:
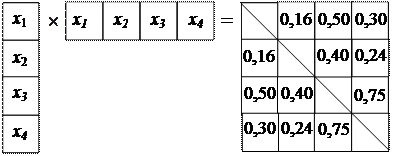
Анализ корреляционной матрицы показывает, что переменная 1 значительно коррелирует с переменными 2 и 3; переменная 2 достоверно коррелирует с переменной 3, а переменная 3 – с переменной 4. Задача факторного анализа является как бы обратной по отношению к задаче умножения двух матриц, одна из которых является столбцом, а другая – строкой. Она сводится к тому, чтобы по уже имеющейся матрице парных корреляций отыскать одинаковые, по включенным в них числам, столбец и строку, умножение которых друг на друга порождает корреляционную матрицу. Иллюстрация:
Здесь х 1, х 2, х 3 и х 4 – искомые числа. Для их определения существуют специальные математические процедуры и программы для ЭВМ. Допустим, что мы уже нашли эти числа: х 1 = 0,45, х 2 = 0,36, х 3 = 1,12 и х 4 = 0,67. Совокупность найденных чисел и называется фактором, а сами эти числа – факторными весами ли нагрузками. От факторов можно перейти к содержательной интерпретации обнаруженных статистических закономерностей. Фактор содержит в себе ту же самую информацию, что и вся корреляционная матрица, а факторные нагрузки соответствуют коэффициентам корреляции. В нашем примере переменная х 3 имеет наибольшую факторную нагрузку (1,12), а х 2 – наименьшую (0,36). Следовательно, влияние х 3 на все переменные является наиболее значимым, а влияние х 2 – наименее значимым. Из корреляционной матрицы видно, что связи переменной х 3 со всеми остальными являются наиболее сильными (от 0,40 до 0,75), а переменной х 2 – самыми слабыми (от 0,16 до 0,40).
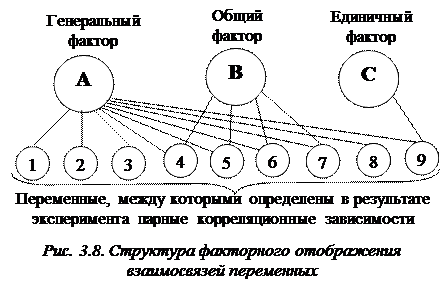
Чаще всего в итоге факторного анализа определяются не один, а несколько факторов, по-разному объясняющих матрицу интеркорреляции переменных. В таком случае факторы делят на генеральные, общие и единичные. Генеральными называются факторы, все факторные нагрузки которых значительно отличаются от нуля (нуль нагрузки свидетельствует о том, что данная переменная никак не связана с остальными и не оказывает на них никакого влияния). Общие – это факторы, у которых часть факторных нагрузок отлична от нуля. Единичные – это факторы, у которых существенно отличается от нуля только одна из нагрузок. На рис. 3.8 схематически представлена структура факторного отображения переменных в факторах различной степени общности. Отрезки, соединяющие факторы с переменными, указывают на высокие факторные нагрузки.
Дискриминантный анализ Предположим, что мы имеем совокупность объектов, разбитую на несколько групп (т. е. для каждого объекта мы можем сказать, к какой группе он относится). Пусть каждый объект имеет несколько количественных признаков. Нужно найти способ, как на основании значений признаков определить группу, к которой следует отнести определенный объект. Например, исследуемыми объектами могут быть пациенты – здоровые или больные той или иной болезнью, а характеристиками – результаты медицинских анализов. Для решения поставленной задачи применяются методы дискриминантного анализа, которые позволяют строить функции от измеряемых признаков, значения которых и определяют разбиение объектов на группы. Желательно, чтобы этих функций (дискриминирующих признаков) было немного – в этом случае результаты анализа легче содержательно истолковать. Особую роль, благодаря своей простоте, играет линейный дискриминантный анализ, в котором классифицирующие признаки выбираются как линейные функции от первичных признаков.
Кластерный анализ Кластерный анализ – это процедура, которая позволяет на основе множества признаков, характеризующих ряд объектов, сгруппировать их в классы (кластеры) так, чтобы объекты, входящие в один класс, были более однородными, чем объекты, входящие в другие классы. Группировка происходит на основе вычисления расстояний между объектами в различных метриках по числовым значениям признаков. Большинство методов кластеризации (иерархической группировки) являются аггломеративными (объединительными) – они начинаются с создания элементарных кластеров, каждый из которых состоит ровно из одного исходного наблюдения (одной точки), а на каждом последующем шаге происходит объединение двух наиболее близких кластеров в один. Момент остановки этого процесса может задаваться исследователем (например, указанием требуемого числа кластеров или максимального расстояния, при котором допустимо объединение). Графическое изображение процесса объединения кластеров может быть получено с помощью дендрограммы – дерева объединения кластеров. Другие методы кластерного анализа являются дивизивными – они пытаются разбивать объекты на кластеры непосредственно. Методы кластеризации довольно разнообразны, в них по-разному выбирается способ определения близости между кластерами (и между объектами), а также используются различные алгоритмы вычислений. Заметим, что результаты кластеризации зависят от выбранного метода, и эта зависимость тем сильнее, чем менее явно изучаемая совокупность разделяется на группы объектов. Поэтому результаты вычислительной кластеризации могут быть дискуссионными. Иногда результаты кластеризации можно обосновать с помощью методов дискриминантного анализа. Методы одномерного и многомерного статистического анализа данных можно реализовать на компьютере с помощью универсальных статистических пакетов STADIA, STATGRAFICS, SYSTAT, а также специализированных пакетов, имеющих большие возможности как в смысле размерности многомерных методов, так и графические.
Упражнения для самопроверки 1. Записать в виде вариационного и статистического рядов выборку 27, 28, 31, 30, 26, 34, 39, 35, 28, 32, 30, 33, 30, 36, 36 значений признака Х. Найти: 1) размах выборки; 2) относительные частоты; 3) моду; 4) медиану. Построить: 1) график эмпирической функции распределения выборки; 2) полигон частот; 3) полигон относительных частот; 4) гистограмму частот. Найти: 1) точечные оценки числовых характеристик 2. На уровне значимости
3. Компания, производящая средства для потери веса, утверждает, что прием таблеток в сочетании со специальной диетой позволяет сбросить в среднем в неделю 400 г веса. Случайным образом отобраны 25 человек, использующих эту терапию, и обнаружено, что в среднем еженедельная потеря в весе составила 430 г со средним квадратическим отклонением 110 г. Проверьте гипотезу о том, что средняя потеря в весе составляет 400 г. Уровень значимости
4. С помощью некоторой психолого-диагностической методики определена величина интереса к изучению некоторого предмета у 12 студентов: 5,3; 6,0; 7,1; 8,1; 4,3; 8,3; 7,4; 2,5; 9,0; 5,7; 3,6; 6,8. Тестовые баллы этих же студентов на экзамене оказались соответственно равны: 12; 15; 17; 20; 10; 25; 16; 9; 23; 11; 14; 21. Проверить гипотезу о статистической зависимости тестовых баллов студентов от их интереса к предмету.
ЗАКЛЮЧЕНИЕ В пособии рассмотрены лишь основные понятия и теоремы теории вероятностей и математической статистики, многие утверждения и теоремы приведены без доказательства. Более широкое и подробное изложение курса читатель может найти в литературе, список которой прилагается. БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Кремер Н. Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2001. – 543 с. 2. Вентцель Е. С. Теория вероятностей: Учебник для вузов. – 7-е изд, стер. – М.: Высш. шк., 2001. – 575 с. 3. Вентцель Е. С., Овчаров Л. А. Теория вероятностей и ее инженерные приложения. Учеб. пособие для втузов. – 2-е изд., стер.– М.: Высш. шк., 2000.– 480 с. 4. Гмурман В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов. – Изд. 7-е, стер. – М.: Высш. шк., 2001. – 479 с. 5. Романовский Р. К., Романовская А. М. Элементы теории вероятностей и математической статистики (теория и задачи). – Омск: Издательство «Наследие», Диалог – Сибирь, 2003. – 172 с. 6. Немов Р. С. Психология: Учеб. для студ. высш. пед. заведений: В 3 кн. – М.: ВЛАДОС, 2000. – Кн. 3. – 640 с. 7. Ниворожкина Л. И., Морозова З. А., Герасимова И. А., Житникова И. В. Основы статистики с элементами теории вероятностей для экономистов: Руководство для решения задач.– Ростов н/Д: Феникс, 1999. – 320 с. 8. Тюрин Ю. Н., Макаров А. А. Анализ данных на компьютере / Под ред. В. Э. Фигурнова. – М.: ИНФРА-М, Финансы и статистика, 1995.– 384 с. 9. Красс М. С., Чупрынов Б. П. Основы математики и ее приложения в экономическом образовании: Учеб. – М.: Дело, 2000. – 688 с.
ПРИЛОЖЕНИЯ
1. Таблица значений функции Гаусса
И её график
3. Таблица значений функции Пуассона
4. Таблица квантилей распределения И график функции
Окончание прил. 4
|
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 348; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.177.204 (0.024 с.) |

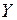 .Пусть признак Х имеет r градаций (уровней)
.Пусть признак Х имеет r градаций (уровней)  , признак
, признак  градаций
градаций 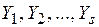 . Обозначим через
. Обозначим через  частоту события
частоту события  Выборочные частоты представляют в виде таблиц, называемых таблицами сопряженности
Выборочные частоты представляют в виде таблиц, называемых таблицами сопряженности
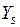
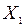
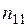
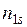



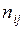 вычисляют статистику (существуют различные методы) и определяют, зависимы или нет признаки Х и
вычисляют статистику (существуют различные методы) и определяют, зависимы или нет признаки Х и 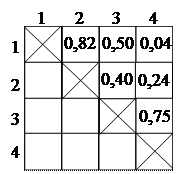
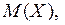
 признака Х; 2) интервальные оценки числовых характеристик
признака Х; 2) интервальные оценки числовых характеристик 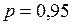 .
.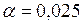 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:
проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты: .
. и её график
и её график
 2. Таблица значений функции Лапласа
2. Таблица значений функции Лапласа 


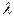 m
m
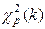

 k
k



