
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Повторные испытания. Схема БернуллиСодержание книги
Поиск на нашем сайте
Рассмотрим часто встречающуюся ситуацию. 1. Проводится n независимых испытаний. Независимость означает, что в каждом следующем испытании полностью повторяются условия, в которых проводилось предыдущее. 2. В каждом испытании интересующее нас событие А (успех) наступает с одной и той же вероятностью р, и не наступает, т. е. наступает событие Указанная ситуация – схема повторных испытаний (схема Бернулли). Пусть k – число наступлений события А (число успехов) в серии из n независимых испытаний. Очевидно, что в зависимости от случая k принимает одно из возможных значений Обозначим Теорема. Вероятность числа успехов k в серии из n повторных испытаний находится по формуле Бернулли:
где p – вероятность успеха, q – вероятность неуспеха. Доказательство:
В сумме перечислены всевозможные n-ки (произведения n элементов), в которых на k местах стоит множитель А и на (n – k) местах – множитель
поскольку множители в составе каждого слагаемого независимы, вероятность каждого слагаемого – Пример. Вероятность изготовления на станке стандартной детали равна 0,8. Найти вероятность возможного числа бракованных деталей среди пяти отобранных. Решение. Испытание – проверка детали на стандартность. Обозначим события:
Полученные вероятности изобразим точками с координатами Наивероятнейшее число появлений успеха В схеме повторных испытаний В последнем примере мы видим, что есть значения k (в данном случае Теорема. Наивероятнейшее число
причем таких Доказательство: 1. Докажем, что таких
Так как 2. По определению наивероятнейшего числа:
Из неравенства (1) с учетом формул Бернулли и числа сочетаний имеем:
После почленного деления на
Умножая обе части неравенства на выражение
Отсюда
Аналогично из неравенства (2) системы получаем Пример 1. В условиях примера п. 1.8
Так как
Пример 2. Сколько раз необходимо подбросить игральную кость, чтобы наивероятнейшее число выпадений трёх очков было равно 10? Решение. Пусть событие Наивероятнейшее число успехов
Отсюда
Схема повторных испытаний. Формулы приближенных Вычислений
Если число испытаний Теорема 1. Формула Пуассона. Если вероятность успеха в каждом испытании стремится к нулю
Эта приближенная формула дает незначительные погрешности, если
Пример 1. Швейной фабрикой выпускаются два вида пальто с меховым воротником и без него. Пальто с меховым воротником составляют 0,01% от всего объема выпускаемых изделий. Найти вероятность того, что из 100 тыс. пальто, изделий с меховым воротником окажется только два. Решение. В этом примере n достаточно велико: Пусть событие А – пальто с меховым воротником, тогда вероятность успеха Параметр, Тогда по формуле Пуассона (1.18):
Ответ: примерно в 0,2% случаев из 100 тыс. пальто два окажутся с меховым воротником.
Правую часть приближенной формулы можно рассматривать как функцию двух переменных
Эта функция называется функцией Пуассона, для нее существуют таблицы (см. табл. П.3). Пример 2. На факультете насчитывается 1825 студентов. Какова вероятность, что 1 сентября является днем рождения одновременно четырех студентов? Решение. Из условия задачи
|
|||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1064; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.151.11 (0.01 с.) |

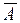 (неуспех), с вероятностью q = 1– p.
(неуспех), с вероятностью q = 1– p. .
.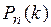 – вероятность k успехов в серии из n испытаний.
– вероятность k успехов в серии из n испытаний. , (1.16)
, (1.16) .
. , все слагаемые суммы – попарно несовместные события, тогда по формулам (1.12), (1.9) получаем:
, все слагаемые суммы – попарно несовместные события, тогда по формулам (1.12), (1.9) получаем:
 , а всего слагаемых –
, а всего слагаемых –  – деталь стандартная (неуспех); А – деталь бракованная (успех).
– деталь стандартная (неуспех); А – деталь бракованная (успех). , k = 0, 1, 2, 3, 4, 5 – число бракованных деталей,
, k = 0, 1, 2, 3, 4, 5 – число бракованных деталей,  ,
, 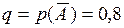 . По формуле (1.16):
. По формуле (1.16): ;
; ;
; ;
; ;
; ;
;  .
.
 . Соединив эти точки ломаной, получим полигон распределения вероятностей (рис. 1.8).
. Соединив эти точки ломаной, получим полигон распределения вероятностей (рис. 1.8). ), обладающие наибольшей вероятностью
), обладающие наибольшей вероятностью  наступления события А в
наступления события А в  независимых испытаниях называется наивероятнейшим, если
независимых испытаниях называется наивероятнейшим, если 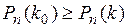 , для
, для 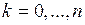 .
. , (1.17)
, (1.17)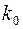 не более двух.
не более двух. , длина этого промежутка равна
, длина этого промежутка равна

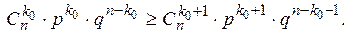
 получим
получим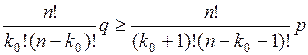 .
. , после упрощений получим неравенство
, после упрощений получим неравенство или
или 


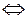
 .
. , т. к.
, т. к.  .
. . Из полученных оценок для
. Из полученных оценок для 


 . Наивероятнейшее число
. Наивероятнейшее число 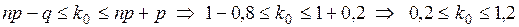 .
. – выпадение тройки (успех); тогда
– выпадение тройки (успех); тогда 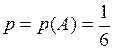 ,
,  .
.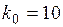 , найдем общее число испытаний
, найдем общее число испытаний  по оценке (1.17):
по оценке (1.17):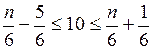 или
или 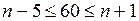 .
. , т. е. для того, чтобы наивероятнейшее число выпавших троек было равно 10, необходимо подбросить игральную кость от 59 до 65 раз.
, т. е. для того, чтобы наивероятнейшее число выпавших троек было равно 10, необходимо подбросить игральную кость от 59 до 65 раз.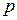 и
и  – дробные числа. Поэтому рассмотрим приближенные формулы вычисления
– дробные числа. Поэтому рассмотрим приближенные формулы вычисления  .
. при неограниченном увеличении числа испытаний
при неограниченном увеличении числа испытаний 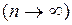 и произведении
и произведении 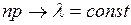 , то вероятность
, то вероятность 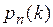 удовлетворяет следующему соотношению:
удовлетворяет следующему соотношению: . (1.18)
. (1.18) .
. .
. =
= 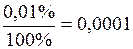 .
.
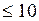 .
. .
. :
: .
. ,
,  ,
, 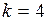 .
. .
.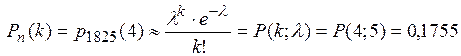 (табл. П. 3).
(табл. П. 3).


