
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центральная предельная теоремаСодержание книги
Поиск на нашем сайте
Центральная предельная теорема – это группа теорем об условиях, при которых возникает нормальный закон распределения. При изучении нормального закона была сформулирована теорема: если
для любого сколь угодно малого числа Замечательным является то, что это утверждение остается верным при большом числе слагаемых, если отбросить требование нормальности. Это утверждение называется центральной предельной теоремой и кратко формулируется так: сумма большого числа независимых однотипных случайных величин с любым законом распределения приближенно нормальна. Впервые центральная предельная теорема была получена в XIX веке немецким математиком Линдебергом. Позднее русским математиком А. М. Ляпуновым этот результат был значительно усилен: оказалось, что требование одинакового закона распределения слагаемых не обязательно. Кратко теорема Ляпунова формулируется так: если случайные величины независимы и никакая из них не доминирует над другими, то при достаточно большом числе слагаемых их сумма приближенно нормальна. Наиболее общая формулировка центральной предельной теоремы была дана советским ученым С. М. Бернштейном. Центральная предельная теорема объясняет широкое распространение нормального закона в природе. Действительно, в ряде случаев случайные величины представляют собой результат наложения большого числа независимых случайных факторов, каждый из которых не доминирует над остальными, поэтому такие случайные величины практически нормально распределены.
Упражнения для самопроверки
1. Из коробки с шестью деталями, среди которых четыре стандартные, наудачу взяты три детали. Составить закон распределения дискретной случайной величины Х – количества стандартных деталей среди отобранных.
2. Случайная составляющая дохода равна 2 Х, а случайная составляющая затрат равна 50 Y. Найти дисперсию прибыли при условиях: величина Х распределена по биномиальному закону с параметрами: n = 100, p = 0,5; величина Y распределена по закону Пуассона с параметром λ = 2; случайные величины X и Y являются независимыми.
Ответ: 5010
3. Найти дисперсию дискретной случайной величины Х – числа отказов элемента некоторого устройства – в 10 независимых опытах, если вероятность отказа элемента в каждом опыте равна 0,9. Ответ: 0,9
4. Непрерывная случайная величина Х задана на всей оси Ох функцией распределения Ответ: 0,25
5. Случайная величина Х задана функцией распределения
Найти вероятность того, что Х примет значения: а) не менее 0,2; б) менее трёх; в) не менее трёх; г) не менее пяти. Ответ: а) 0; б) 0,5; в) 0,5; г) 0. 6. Дана плотность распределения непрерывной случайной величины Х:
Найти функцию распределения F(x).
7. Случайная величина X задана на интервале (0; 5) плотностью распределения
8. Найти дисперсию и среднее квадратическое отклонение случайной величины Х, распределенной равномерно в интервале (2; 8). Ответ:
9. Размер мужских сорочек является случайной величиной с нормальным законом распределения, математическим ожиданием 39 и дисперсией 9. Какой процент от общего объема заказа следует предусмотреть магазину для сорочек 40-го размера воротничка при условии, что этот размер находится в интервале (39,5; 40,5)? Ответ: 12,6%.
10. Найти формулу плотности вероятности нормально распределенной случайной величины Х, если математическое ожидание равно 3, а дисперсия равна 16. Ответ:
11. Случайная величина Х распределена нормально с математическим ожиданием Ответ: 0,2.
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 410; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.218.124 (0.007 с.) |

 – независимые нормальные случайные величины с одними и теми же параметрами
– независимые нормальные случайные величины с одними и теми же параметрами 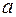 и
и 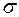 , то их сумма
, то их сумма  также нормальна и имеет параметры
также нормальна и имеет параметры  и
и  . Кроме того, справедливо равенство
. Кроме того, справедливо равенство Ф
Ф 
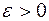 . Это равенство практически точно уже при
. Это равенство практически точно уже при  .
. . Найти вероятность того, что величина Х примет значение, заключенное в интервале (0; 1).
. Найти вероятность того, что величина Х примет значение, заключенное в интервале (0; 1).

 ; вне этого интервала
; вне этого интервала  . Найти дисперсию Х. Ответ: 25/18.
. Найти дисперсию Х. Ответ: 25/18.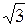 .
.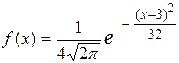 .
.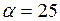 . Вероятность попадания Х в интервал (10;15) равна 0,2. Найти вероятность попадания Х в интервал (35; 40).
. Вероятность попадания Х в интервал (10;15) равна 0,2. Найти вероятность попадания Х в интервал (35; 40).


