
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Локальная формула Муавра-ЛапласаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Укажем без доказательств удобную приближенную формулу вычисления Теорема 2. Если вероятность успеха
где Эта формула дает незначительную погрешность, если
1) функция четная, т.е.
2) функция монотонно убывает при положительных значениях х, причем
3) площадь, заключенная между осью Ох и графиком функции Гаусса равна единице. Пример 3. В некоторой местности из каждых 100 семей 80 имеют холодильники. Найти вероятность того, что из 400 семей 300 имеют холодильники. Решение.
Пример 4. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2. Решение.
можно применить формулу Муавра-Лапласа (1.19):
Формула Бернулли приводит примерно к такому же результату:
Пример 5. Вероятность поражения мишени при одном выстреле равна 0,75. Найти вероятность того, что мишень будет поражена 8 раз при 10 выстрелах. Решение.
По формуле (1.19):
По формуле Бернулли:
Расхождение объясняется тем, что n достаточно мало и Интегральная формула Лапласа Теорема 3. В схеме Бернулли при большом числе испытаний n, если
где Формула (1.20) называется интегральной формулой Лапласа, она дает малую погрешность, если Свойства функции Лапласа Ф (x) По определению функция Лапласа Ф(x) – этоплощадь криволинейной трапеции, опирающейся на отрезок [0; x], и ограниченной сверху функцией Гаусса
1) Ф(x) нечетная, т. е.
Ф(–x) = – Ф(x);
2) Ф(x) возрастает на всей числовой оси;
3) Последнее свойство следует из свойств функции Гаусса и геометрической интерпретации функции Лапласа, причем
с учетом нечетности Ф(x)(рис. 1.11). Пример 6. Из каждых 100 семей 80 имеют холодильник.
Решение. По условию задачи и:
Используя формулу (1.20), получаем:
Следствия интегральной формулы Лапласа Следствие 1
Доказательство:
Следствие 2
Доказательство:
Пример 7. Сколько нужно провести опытов, чтобы с вероятностью 0,901 утверждать, что частота интересующего нас события будет отличаться по абсолютной величине от вероятности появления этого события, равной 0,4, не более чем на 0,1? Решение. Если
Отсюда
По таблицам значений функции Лапласа (табл. П. 2), по значению Ф(х) = 0,4505, находим значение аргумента х:
Так как Отсюда имеем С учетом целочисленности n получаем Итак, нужно провести не менее 66 опытов, чтобы с вероятностью 0,901 частота интересующего нас события отличалась по абсолютной величине от вероятности появления этого события не более, чем на 0,01.
Упражнения для самопроверки 1. Два букиниста обмениваются друг с другом парами книг. Найти число способов обмена, если первый букинист обменивает 6 книг, а второй – 8 книг. Ответ: 588
2. Абонент забыл две промежуточные цифры номера телефона и набрал их наугад. Найти вероятность того, что номер набран правильно в случаях: а) две разные цифры расположены в номере рядом; б) обе цифры расположены в разных местах, за исключением первой позиции. Ответ: а) 1/45; б) 0,01
3. В урне 40 шаров: 15 белых, 15 красных и 10 синих. Найти вероятность появления цветного шара. Ответ: 0,47
4. Абонент забыл первую цифру телефонного номера. Найти вероятность того, что при наборе номера наудачу он наберет его верно не более чем с трёх попыток. Ответ:0,38
5. В лотерее разыгрывается 200 вещевых и 50 денежных выигрышей на каждые 10 тыс. билетов. Чему равна вероятность выигрыша вообще? Ответ: 0,025
6. В читальном зале имеется 6 учебников, из которых три нового выпуска. Читатель последовательно, один за другим, взял два учебника. Найти вероятность того, что обе взятые книги нового выпуска.
Ответ: 0,2
7. В автохозяйстве имеются две автоцистерны. Вероятность технической неисправности этих машин составляет соответственно 0,9 и 0,8. Найти вероятность исполнения работы второй автоцистерной заказчику, сделавшему накануне заказ на автоцистерну. Ответ: 0,4
8. Инвестор решил вложить поровну средства в три предприятия при условии возврата ему через определенный срок 150% от вложенной суммы каждым предприятием. Вероятность банкротства каждого из предприятий 0,2. Найти вероятность того, что по истечении срока кредитования инвестор получит обратно, по крайней мере, вложенную сумму. Ответ: 0,896 9. Три стрелка выстрелили залпом по цели, и две пули поразили её. Найти вероятность того, что первый стрелок поразил цель, если вероятности попадания в цель стрелками соответственно равны 0,4, 0,3 и 0,5. Ответ: 0,69
10. Определить, что вероятнее для соперников равной силы при игре в шахматы: выиграть одну партию из двух или две партии из четырёх. Ответ: выигрыш одной партии из двух.
11. Вероятность появления события равна 0,7 в каждом из 2100 независимых испытаний. Найти вероятность появления события: а) не менее 1470 раз; б) не менее 1470 и не более 1500 раз; в) не более 1469. раз. Ответ: а) 0,4239; б) 0,5; в) 0,5.
12. Вероятность обращения в поликлинику каждого взрослого человека в период эпидемии гриппа равна 0,8. Найти, среди какого числа взрослых человек можно ожидать, что в поликлинику будет не менее 75 обращений. Ответ: 95
13. В банке, осуществляющем кредитование населения, 1000 клиентов. Каждому из клиентов выдается кредит 500 тыс. р. При условии возврата 110% от этой суммы. Вероятность невозврата кредита каждым из клиентов, в среднем составляет Ответ: а) 44,5 млн. р.; б) 40,5 млн. р.
14. Вероятность появления события в каждом из 900 независимых испытаний равна 0,5. Найти вероятность отклонения относительной частоты появления события от его вероятности не более чем на 0,02 по абсолютной величине. Ответ:0,7698
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 2.1. Понятие случайной величины. Закон распределения В первой части пособия приводились примеры событий, состоящих в появлении значений той или иной числовой величины. Например, полученная студентом на экзамене оценка, может быть равной числам 2, 3, 4 и 5. Заранее определить оценку однозначно невозможно, поскольку она зависит от многих причин, которые полностью не могут быть учтены. В этом смысле полученная оценка есть величина случайная; числа 2, 3, 4 и 5 – возможные значения этой величины. Если с испытанием связана некоторая величина, значение которой зависит от случая, то эта величина называется случайной. Приведем несколько примеров случайных величин: 1) число успехов в схеме Бернулли; 2) продолжительность бесперебойной работы компьютера; 3) число купленных путевок в туристической фирме за определенный промежуток времени; 4) результат измерения некоторой величины с помощью прибора. Случайная величина называется дискретной, если она принимает отдельные значения с определенной вероятностью. Число определенных значений дискретной случайной величины может быть конечным и бесконечным, но счетным. Непрерывной случайной величиной называют величину, значения которой полностью заполняют некоторый конечный или бесконечный промежуток на числовой оси.
В приведенных примерах случайные величины 1) и 3) – дискретные; 2) и 4) – непрерывные. Случайные величины будем обозначать заглавными буквами X, Y, …, а их возможные значения – строчными буквами x, y, … Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Этот закон можно задать таблицей, аналитически (формулой) или графически.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 3337; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.207.176 (0.014 с.) |

 . Эта формула была получена для частного случая
. Эта формула была получена для частного случая  Муавром в 1730 г. и обобщена для общего случая
Муавром в 1730 г. и обобщена для общего случая 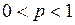 Лапласом в 1785 г.
Лапласом в 1785 г. в каждом испытании постоянна и отлична от 0 и 1, то при достаточно больших значениях n
в каждом испытании постоянна и отлична от 0 и 1, то при достаточно больших значениях n , (1.19)
, (1.19) – функция Гаусса,
– функция Гаусса, 
 .
. Для функции Гаусса
Для функции Гаусса 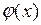 (рис. 1.9) имеются таблицы (табл. П.1), пользуясь которыми нужно иметь в виду следующие свойства функции Гаусса:
(рис. 1.9) имеются таблицы (табл. П.1), пользуясь которыми нужно иметь в виду следующие свойства функции Гаусса: ;
; .
. при
при 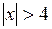 ;
; – вероятность успеха;
– вероятность успеха; 
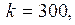
 . Тогда
. Тогда  , значит можно применять формулу (1.16):
, значит можно применять формулу (1.16):
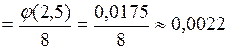 (табл. П.1).
(табл. П.1). .
. , следовательно,
, следовательно,
 .
. 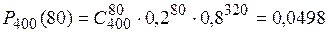 .
.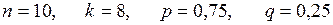 .
.
 .
.
 , то справедлива приближенная формула
, то справедлива приближенная формула , (1.20)
, (1.20) – функция Лапласа.
– функция Лапласа. Для функции имеются таблицы (см. табл. П. 2).
Для функции имеются таблицы (см. табл. П. 2). Свойства функции Ф(x):
Свойства функции Ф(x):
 при
при  .
. 
 Найти вероятность того, что от 300 до 360 (включительно) семей из 400 имеют холодильники.
Найти вероятность того, что от 300 до 360 (включительно) семей из 400 имеют холодильники.

 . (1.21)
. (1.21)

 . (1.22)
. (1.22)

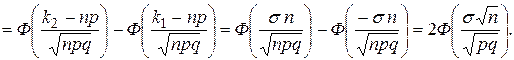
 , то
, то  . Используя условие задачи и следствие 2, получаем:
. Используя условие задачи и следствие 2, получаем: .
.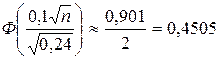 .
. , т.е.
, т.е.  .
. , то
, то  .
. ,
,  , следовательно
, следовательно 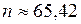 .
. .
. . Какая прибыль гарантирована банку с вероятностью: а) 0,8; б) 0,995?
. Какая прибыль гарантирована банку с вероятностью: а) 0,8; б) 0,995?


