
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретная случайная величинаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Закон распределения дискретной случайной величины Закон распределения дискретной случайной величины – это таблица, состоящая из двух строк. Первая указывает возможные значения случайной величины, а вторая – их вероятности.
Поскольку в каждом испытании случайная величина принимает ровно одно из возможных значений, то события
Если множество возможных значений дискретной случайной величины Х бесконечно, то ряд
Пример 1. В денежной лотерее разыгрываются 100 билетов. Один выигрыш – в 200 руб., два выигрыша – в 100 руб. и 10 выигрышей – по 10 руб. Составить закон распределения чистого выигрыша, полученного участником лотереи, купившим один билет по цене 5 руб. Решение. Пусть случайная величинаХ – чистый выигрышучастника лотереи. Возможные значения
Таким образом, искомый закон распределения имеет вид
Пример 2. Пакет из 8 документов содержит 5 правильно оформленных документов. Наугад отбирают 3 документа. Составить закон распределения случайной величины Х – числа правильно оформленных документовсреди трех отобранных. Решение. Случайная величина Х может принимать четыре возможных значения: 0, 1, 2, 3. Вероятность того, что правильно оформлены m документов среди трех отобранных, определяется формулой
Варьируя значения
Пример 3. Вероятностный прогноз для величины Х – процентного изменения стоимости акций по отношению к их текущему курсу в течение шести месяцев, имеет закон распределения
Найти вероятность того, что покупка акций будет более выгодна, чем помещение денег на банковский депозит под 36% годовых. Решение. Прирост на банковском депозите при условии 3% в месяц (т. к. годовой – 36%) составит через шесть месяцев
Вероятность того, что покупка акций выгоднее банковского депозита, определяется суммой вероятностей, соответствующих более высокому росту курса акций:
т. е. в 60% случаев покупка акций более выгодна, чем помещение денег на банковский депозит. Числовые характеристики дискретной случайной величины Закон распределения полностью характеризует случайную величину. Однако, в ряде случаев при решении практических задач достаточно знать числовые характеристики случайной величины (математическое ожидание, дисперсию, среднее квадратическое отклонение и др.), которые дают некоторое приближенное описание случайной величины. Математическое ожидание дискретной случайной величины
Пусть с испытанием связана дискретная случайная величина Х с законом распределения
Математическим ожиданием дискретной случайной величины Х называется сумма всех произведений её возможных значений на их вероятности:
Отсюда следует, что математическое ожидание есть некоторая постоянная (неслучайная) величина, которая характеризует среднее значение случайной величины с учетом не только её возможных значений, но и их вероятностей. Например, в примере 1 п. 2.2.1
т. е. среднеожидаемый чистый выигрыш участника лотереи равен 0.
Пример. Мишень разбита на восемь секторов и установлена так, что может вращаться вокруг своей оси. При достаточно большой скорости вращения стрелок не может различать цифры и стреляет наугад. При попадании в сектор с номером 1 стрелок выигрывает один рубль, в сектор с номером 2 – 2 руб. и т. д. Стоит ли участвовать в такой игре, если за право стрелять один раз надо платить 5 руб.? Решение. Поскольку мишень вращается, то способности стрелка не имеют никакого значения, т. е. попадание в любой сектор равновозможное. Возможный выигрыш – случайная величина, обозначим её Х. Составим закон распределения этой величины:
Вычислим среднеожидаемый выигрыш:
Так как среднеожидаемый выигрыш в 4,5 руб. меньше платы за выстрел 5 руб., то стрелять много раз явно невыгодно. На основании подобных расчетов организуются различные азартные игры, приводящие игроков к разорению.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 464; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.58.68 (0.006 с.) |

 . (2.1)
. (2.1)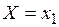 ,
,  ,…,
,…,  образуют полную группу, следовательно, сумма их вероятностей равна единице:
образуют полную группу, следовательно, сумма их вероятностей равна единице:
 сходится и его сумма равна единице:
сходится и его сумма равна единице:
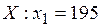 ,
,  ,
,  ,
,  . Соответствующие им вероятности равны:
. Соответствующие им вероятности равны: ;
;  ;
;  ;
; .
. .
. , где
, где  .
.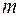 от 0 до 3, получаем искомое распределение:
от 0 до 3, получаем искомое распределение: .
. .
. .
. ,
, .
. (2.2)
(2.2) ,
, .
. .
.


