
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретные случ.величины. Закон распределенияСодержание книги
Поиск на нашем сайте o Случайная величина Х называется дискретной, если она принимает конечное либо счетное число значений, т.е. Ωх—конечно или счетно. o Простейшей формой задания дискретной случайной величины является таблица, в которой перечислены возм-е значения случайной величины и соотв-щие им вероятности.
Табл. называется рядом распр-я дискр-й сл-й вел-ны. Ряд распределения можно изобразить граф-ки. В этом случае по Ох откладывают значения xi, а по Оу —вер-сти pi. Полученные точки соединяют отрезками и получают ломаную, к-я является одной из форм задания закона распределения дискретной величины. o Говорят, что дискретная случайная величина Х имеет биномиальное распределение с параметрами (n,p), если она может принимать целые неотрицательные значения
o .
Обозначим через X дискретную случайную величину—число испытаний, которое нужно провести до первого появления события А. Очевидно, возможными значениями случайной величины Х являются натуральные числа. Пусть в первых k-1 испытаниях событие А не наступало, а в k-ом испытании появилось. Вероятность этого события o Говорят, что случайная величина Х имеет геометрическое распределение с параметром р (0<р<1), если она принимает натуральные значения
Математическое ожидание Свойство 1. К числу важных числовых характеристик относится математическое ожидание, которое приближенно равно среднему значению случайной величины. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Обозначают математическое ожидание случайной величины Х через MX или М(Х). Если случайная величина Х принимает конечное число значений, то Если случайная величина Х принимает счетное число значений, то Математическое ожидание дискретной случайной величины—это неслучайная величина (т.е. число, постоянная). Свойства математического ожидания: 1.Математическое ожидание постоянной величины равно самой постоянной: M(C)=C. Будем рассматривать постоянную С как дискретную случайную величину, которая принимает 1 возможное значение С, с вер-тью =1. Следовательно, Замечание. Произведение постоянной величины С на дискретную случайную величину Х определяется как дискретная случайная величина СХ, возможные значения которой равны произведениям постоянной С на возможные значения Х, вероятности возможных значений СХ равны вероятностям соответствующих возможных значении Х. 2.Постоянный множитель можно выносить за знак математического ожидания: M(CX)=CM(X). Случайные величины X1,X2,…,Xn называются независимыми, если для любых числовых множеств B1,B2,…,Bn Следствие. Мат.ожидание произведения нескольких взаимно незав-х случ-х величин равно произведению их мат. ожиданий.
Следствие. Мат. ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых. Дисперсия o Дисперсией случайной величины называется число o Средним квадратическим отклонением случайной величины Х называется число
Свойства дисперсии. Свойство 1. Дисперсия постоянной величины С равна 0.DC=0.
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
Следствие. Дисперсия суммы нескольких независимых случайных величин равна сумме дисперсий этих величин.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 331; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.23.103 (0.007 с.) |

 Законом распределения дискретной случайной величины Х называется совокупность пар чисел вида (хi, рi), где xi—возможные значения случайной величины, а pi—вероятности, с которыми случайная величина принимает эти значения, т.е.
Законом распределения дискретной случайной величины Х называется совокупность пар чисел вида (хi, рi), где xi—возможные значения случайной величины, а pi—вероятности, с которыми случайная величина принимает эти значения, т.е.  , причем
, причем с вероятностями
с вероятностями  .
.



 Говорят, что случайная величина Х имеет распределение Пуассона с параметром λ (λ>0), если она принимает целые неотрицательные значения
Говорят, что случайная величина Х имеет распределение Пуассона с параметром λ (λ>0), если она принимает целые неотрицательные значения  с вероятностями
с вероятностями



 с вероятностями
с вероятностями 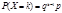 , где q=1-p.
, где q=1-p. .
.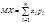 .
. , причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
, причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно. .
. 3.Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
3.Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:  .
. 4.Математическое ожидание суммы двух случайных величин рано сумме математических ожиданий слагаемых:.
4.Математическое ожидание суммы двух случайных величин рано сумме математических ожиданий слагаемых:. . Дисперсия является мерой разброса значений случайной величины вокруг ее математического ожидания.
. Дисперсия является мерой разброса значений случайной величины вокруг ее математического ожидания. .
.
 .
. .
. .
. .
.



