
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равномерное, показательное и нормальное распределение и их характеристики.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте o
Примером равномерно распределенной случ-й вел-ны может служить Х-координата точки, науд. брошенной на [a, b]. o Говорят, что случайная величина Х имеет показательное распределение с параметром λ>0, если она непрерывна и имеет плотность распределения
; обозначают Х~M(λ).
o Говорят, что случайная величинf Х имеет нормальное распределение с параметрами a, G2, если она непрерывна и имеет плотность График плотности нормально распределенной случайной величины имеет вид: o Математическим ожиданием или средним значением непрерывной случайной величины Х с плотностью p(x) называется число o Дисперсией непрерывной случайной величины Х называется число Математическоеожидание и дисперсия непрерывных случайных величин обладают теми же свойствами, что и для дискретных случайных величин.
ТЕОРЕМА О НОРМАЛЬНОМ РАСПРЕД-НИИ. КРИТЕРИИ НЕЗАВИСИМОСТИ ВЕЛИЧИН. Теорема 1. Если случайная величина Х имеет нормальное стандартное распределение с параметрами (a, G2), то случайная величина
Теорема 2. (Критерий независимости дискретных случайных величин). Для того чтобы дискретные случайные величины Х1,…,Хn были независимы, необходимо и достаточно, чтобы для любых действительных чисел х1,…,хn выполнялось соотношение Для того чтобы непрерывные случайные величины Х1, Х2,…,Хn были независимыми, необходимо и достаточно, чтобы для любых действительных чисел х1,…,хn выполнялось соотношение
Здесь
Случайный вектор. Св-ва функции распред-я случ вектора. o Вектор Таким образом, случайный вектор o Функция
Свойства функции распределения случайного вектора. Свойство 1. Свойство 2. Функция распределения случайного вектора неубывающая по каждому аргументу. Пусть x1<y1, тогда событие Тогда Свойство 3.
Свойство 4.
Дискрет и непрерывный случ вектор. Св-ва плотности распределения o Случайный вектор называется дискретным, если все его компоненты—дискретные случайные величины. o Случайный вектор Свойства плотности распределения случайного вектора. Свойство 1. Свойство 2. Свойство 3.
Числовые характеристики системы двух случайных величин. Ковариация, корреляция. Ассиметрия и эксцесс. o Если каждой паре возможных значений случайных величин X и Y соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов X и Y: o Ковариацией между случайными величинами Х и Y называется число,
. o Свойства корреляции. Свойство 1. Абсолютная величина коэффициента корреляции не превосходит единицы, т.е. Свойство 2. Свойство 3. Если случайные величины независимы, то они некоррелированы, т.е. r=0. Пусть Х и Y—независимы, тогда по свойству математического ожидания o Случайные величины Х и Y называют некоррелированными если их коэффициент корреляции равен 0. Замечание. Из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух случайных величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин. o
Знак коэффициента асимметрии указывает на правостороннюю или левостороннюю асимметрию.
o Эксцессом случайной величины Х называется число Характеризует сглаженность кривой распределения по отношению к кривой нормального распределения.
24. Задачи мат.статистики 1)указать сп-бы сбора и группировки стат-х сведений, полученных в рез-те наблюдений или экспериментов. 2)разработать методы анализа стат-х данных в зав-сти от информации. Пусть необходимо изучить сов-сть однородных объектов относительно некоторого кач-го или колич-го признака, характер-щего объект. Выборка -сов-ть случайно отобранных объектов. Генеральная сов-ть – сов-ть объектов, из которых производится выборка. Объем сов-сти – число объектов сов-сти. Выборка должна быть репрезентативной. Пусть можно произвести измерение случ-й величины Х. В п экспериментах результаты измерений х1,х2…хп – некоторые числа. Пусть вып-ся предпосылки: 1.Эксперименты проводят в одинаковых условиях. 2.Эксперименты проводят независимо др.отдруга. Опр: говорят, что рез-ты п экспериментов х1…хп образуют конкретную выборку объема п из генеральной сов-сти случ-й величины Х, если вып-ся предпосылки 1 и 2. Величину Х наз-т теоретической случайной. Пусть треб-ся произвести измерения п случайных величин х1,..хп. Если производить изм-ния сериями, то рез-ты: Х1(1)….Хп(1)-1 серия; Х1(2)…Хп(2)- 2 серия; Х1(к)…Хп(к)-к серия. Тогда случайные величины Х1…Хп – абстрактные рез-ты измерений, т.е. полученные до того, как их провели. Из 1й предпосылки – случайные величины Х1…Хп одинаково распределены и имеют закон распределения, совпадающий с законом распр-я теоретической случ. величины. Из 2й предп – случайные величины независимы. Опр: говорят, что независимые случ.величины х1,..хп образуют абстрактную выборку объема п, если они незав. и одинаково распределены. Опр: функция распр-я F(x) случ-й величины наз. теоретической функцией распределения.
|
|||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 753; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.27 (0.006 с.) |

 Говорят, что случайная величина Х равномерно распределена на отрезке [a, b], если она непрерывна и имеет плотность вероятности:
Говорят, что случайная величина Х равномерно распределена на отрезке [a, b], если она непрерывна и имеет плотность вероятности: Функция распределения равномерно распределенной случайной величины X.
Функция распределения равномерно распределенной случайной величины X.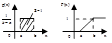



 Функция распределения показательно распределенной случайной величины Х.
Функция распределения показательно распределенной случайной величины Х. . Обозначение Х~N(a, G2), те Х имеет нормальное распределение с параметрами a, G2.
. Обозначение Х~N(a, G2), те Х имеет нормальное распределение с параметрами a, G2.
 при условии, что этот интеграл сходится абсолютно.
при условии, что этот интеграл сходится абсолютно. 
 . Если случайная величина имеет плотность p(x),
. Если случайная величина имеет плотность p(x),  .
. имеет нормальное распределение, т.е.
имеет нормальное распределение, т.е.  .
.
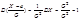 .
. Теорема 3. (Критерий независимости для непрерывных случайных величин).
Теорема 3. (Критерий независимости для непрерывных случайных величин).
 —совместимая плотность распределения случайных величин Х1,…,Хn, то есть совместимая функция распределения случайных величин Х1,…,Хn
—совместимая плотность распределения случайных величин Х1,…,Хn, то есть совместимая функция распределения случайных величин Х1,…,Хn , где
, где  —случайные величины, называются n- мерным случайным вектором.
—случайные величины, называются n- мерным случайным вектором. отображает пространство элементарных исходов Ω→IRn в n-мерное действительное пространство IRn.
отображает пространство элементарных исходов Ω→IRn в n-мерное действительное пространство IRn.
 называется функцией распределения случайного вектора
называется функцией распределения случайного вектора  или совместной функцией распределения случайных величин
или совместной функцией распределения случайных величин  .
.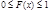 .
. .
. . По свойству вероятности если
. По свойству вероятности если  , то
, то 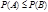 , получим
, получим  . Т.е. функция не убывает по первому аргументу. Аналогично для любого аргумента.
. Т.е. функция не убывает по первому аргументу. Аналогично для любого аргумента. .
.
 .
. называется непрерывным, если существует неотрицательная функция
называется непрерывным, если существует неотрицательная функция  , называется плотностью распределения случайных величин
, называется плотностью распределения случайных величин  такая, что функция распределения
такая, что функция распределения  .
.

 Теорема 1. Пусть
Теорема 1. Пусть  —непрерывный случайный вектор. Тогда случайные величины
—непрерывный случайный вектор. Тогда случайные величины  и
и  —непрерывны, причем
—непрерывны, причем 

 , где
, где  —множество из пространства IRn.
—множество из пространства IRn. .
.
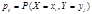 где
где Коэффициентом корреляции между случайными величинами Х и Y называется число.
Коэффициентом корреляции между случайными величинами Х и Y называется число.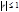 .
. Для того чтобы
Для того чтобы  необходимо и достаточно, чтобы случайные величины Х и Y были связанны линейной зависимостью. Т.е. с вероятностью 1.
необходимо и достаточно, чтобы случайные величины Х и Y были связанны линейной зависимостью. Т.е. с вероятностью 1. Две случайные величины Х и Y называют коррелированными, если их коэффициент корреляции отличен от нуля.
Две случайные величины Х и Y называют коррелированными, если их коэффициент корреляции отличен от нуля. Коэффициентом асимметрии случайной величины Х называется число
Коэффициентом асимметрии случайной величины Х называется число
 .
.


