
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция распределения и плотность распределения непрерывной случайной величины.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Случайная величина Х называется непрерывной, если ее функция распределения непрерывна и имеет производную. Как уже было показано в разделе 4 (формула 4.2), функцией распределения случайной величины Х называется функция F(X), выражающая вероятность выполнения условия
Функция распределения обладает следующими свойствами: 1.Вероятность попадания случайной величины в промежуток от
так как вероятность любого отдельного значения случайной величины равна нулю, если функция распределения непрерывна при этом значении, т. е.:
2.Функция распределения удовлетворяет условиям:
Плотностью распределения (дифференциальной функцией) непрерывной случайной величины называется функция
f(x) = Плотность распределения любой случайной величины неотрицательна: Несобственный интеграл от дифференциальной функции в пределах от -
График функции y = f(x) называется кривой распределения или графиком плотности распределения. Кривая y = f (x) располагается над осью абсцисс. Вероятность попадания случайной величины в промежуток от
Подинтегральное выражение f(x)dx называется элементом вероятности. Оно выражает вероятность попадания случайной точки в промежуток между точками х и Функция распределения F(x) выражается через плотность f(x) формулой:
Математическое ожидание непрерывной случайной величины Х вычисляется по формуле:
дисперсия
Нормальное распределение
Если плотность распределения (дифференциальная функция) случайной переменной определяется выражением:
то говорят, что Х имеет нормальное распределение с параметрами а и
Для расчета вероятности попадания нормально распределенной случайной величины Х в промежуток от
Формула (5.11) иногда в литературе называется интегральной теоремой Лапласа. Функция
3 ) Функция
Формула (5.12) применима и к частоте m, поскольку ее закон распределения при достаточно большом числе испытаний практически совпадает с нормальным. Применительно к случайной величине m, с учетом ее числовых характеристик M(m) = np и формула (5.12) примет вид:
Формула (5.12) может быть применена и к относительной частоте
С вероятностью, очень близкой к единице (равной
В этом состоит правило трех сигм: если случайная величина распределена по нормальному закону, то ее отклонение от математического ожидания практически не превышает Локальная теорема Муавра-Лапласа. При р
Тогда:
для достаточно больших n (здесь
Пример 5.1. На рынок поступила крупная партия говядины. Предполагается, что вес туш - случайная величина, подчиняющаяся нормальному закону распределения с математическим ожиданием а = 950 кг и средним квадратическим отклонением s = 150 кг. Определите вероятность того, что вес случайно отобранной туши: а) окажется больше 1250 кг; б) окажется меньше 850 кг; в) будет находиться между 800 и 1300 кг; г) отклонится от математического ожидания меньше, чем на 50 кг; д) отклонится от математического ожидания больше, чем на 50 кг; е) Найдите границы, в которых отклонение веса случайно отобранной туши от своего математического ожидания не превысит утроенного среднего квадратического отклонения (проиллюстрируйте правило трех сигм); ж) С вероятностью 0,899 определите границы, в которых будет находиться вес случайно отобранной туши. Какова при этом условии максимальная величина отклонения веса случайно отобранной туши от своего математического ожидания? Решение. а) Вероятность того, что вес случайно отобранной туши окажется больше 1250 кг – можно понимать как вероятность того, что вес случайно отобранной туши окажется в интервале от 1250 кг до +∞. Формула расчета вероятности попадания в заданный интервал нормально распределенной случайной велечины Х имеет вид:
где Ф0(z) - функция Лапласа:
Функция Ф0(z) является нечетной функцией; т.е. Ф0(-z) = -Ф0(z). Найдем вероятность того, что вес случайно отобранной туши окажется больше 1250 кг. По условию: a = 1250, b = +¥, а = 950, s = 150. Используем формулу расчета вероятности попадания в заданный интервал нормально распределенной случайной величины Х.
Найдем по таблице функции Лапласа (Приложение 2) значения Ф0(z). Значения Ф0(+¥) в таблице нет. Однако известно, что Ф0(z) ® 0,5 при z ® + ¥.Уже при z = 5 Ф0(z = 5) = 0,49999997» 0,5. Очевидно, что Ф0(+¥) - величина бесконечно близкая к 0,5. Ф0(-¥) - величина бесконечно близкая к -0,5. По таблице функции Лапласа Ф0(2) = 0,47725. Отсюда: P(X>1250) = 0,5 - 0,47725 = 0,02275. Итак, вероятность того, что вес случайно отобранной туши окажется больше 1250 кг, составляет 0,02275. Проиллюстрируем решение задачи графически (рис.5.1).
Рис.5.1 Графическая интерпретация к примеру 5.1. Итак, нам задана нормально распределенная случайная величина Х с математическим ожиданием а = 950 кг. и средним квадратическим отклонением s = 150 кг., то есть Х ~N(950;1502). Мы хотим найти вероятность того, что Х больше 1250, то есть определить Р(Х > 1250). Преобразуем Х в Z, и тогда искомая вероятность определится по таблице Приложения 2 стандартного нормального распределения. Точка z = 0 соответствует математическому ожиданию, то есть а = 950 кг. б) Вероятность того, что вес случайно отобранной туши окажется меньше 850 кг - это, то же самое, что вероятность того, что вес случайно отобранной туши окажется в интервале от -¥ до 850 кг. По условию: a = -¥, b = 850, а = 950, s = 150. Для расчета искомой вероятности используем формулу расчета вероятности попадания в заданный интервал нормально распределенной случайной величины Х.
Согласно свойству функции Лапласа: -Ф0(-¥) = Ф0(+¥), а Ф0(-0,67) = -Ф0(0,67). Найдем по таблице функции Лапласа (Приложение 2) значения Ф0(z). Ф0(+¥)» 0,5; Ф0(0,67) = 0,24857. Отсюда: P(X < 850) = 0,5 - 0,24857 = 0,25143. Вероятность того, что вес случайно отобранной туши окажется меньше 850 кг составляет 0,25143. Проиллюстрируем решение задачи графически (рис. 5.2).
Рис.5.2. Графическая интерпретация к примеру 5.1.
По условию данной задачи точка на оси абсцисс (z = -0,67) соответствует х = 850, т.е. весу, равному 850 кг. Заштрихованная на графике площадь представляет собой вероятность того, что вес наудачу выбранной туши окажется меньше 850 кг, т.е. в интервале от -¥ до 850 кг. в) Найдем вероятность того, что вес случайно отобранной туши окажется в интервале от 800 до 1300 кг. По условию: a = 800, b = 1300, а = 950, s = 150. Для расчета искомой вероятности используем формулу расчета вероятности попадания в заданный интервал нормально распределенной случайной величины Х.
Согласно свойству функции Лапласа: -Ф0(-1) = Ф0(1). Найдем по таблице функции Лапласа (Приложение 2) значения Ф0(z). Ф0(2,33) = 0,49010; Ф0(1) = 0,34134. Отсюда: P(800 < X< 1300) = 0,49010 + 0,34134 = 0,83144. Вероятность того, что вес случайно отобранной туши окажется в интервале от 800 кг до 1300 составляет 0,83144.
Проиллюстрируем решение задачи графически (рис. 5.3).
Рис.5.3. Графическая интерпретация к примеру 5.1.
По условию данной задачи точка на оси абсцисс (z = -1) соответствует х = 800, т.е. весу, равному 800 кг, а точка (z = 2,33) соответствует х = 1300, т.е. весу, равному 1300 кг. Заштрихованная на графике площадь представляет собой вероятность того, что вес наудачу выбранной туши окажется в интервале от 800 до 1300 кг. На графике видно, что искомую вероятность, что вес наудачу выбранной туши окажется в интервале от 800 до 1300 кг, можно было найти другим способом. Для этого необходимо было найти вероятность того, вес наудачу выбранной туши окажется меньше 800 кг, а также- больше 1300 кг, Полученные вероятности – сложить и вычесть из единицы. Так, вероятность того, вес наудачу выбранной туши окажется меньше 800 кг - это, другими словами, вероятность того, что вес случайно отобранной туши окажется в интервале от -¥ до 850 кг.
Вероятность того, что вес случайно отобранной туши окажется больше 1300 кг - это, другими словами, вероятность того, что вес случайно отобранной туши окажется в интервале от 1300 кг до +¥.
Отсюда, искомая вероятность того, что вес наудачу выбранной туши окажется в интервале от 800 до 1300 кг: Р(800 < Х < 1300) = 1 - (P(X<800) + P(X>1300)) = 1 - (0,15866 + 0,0099) = =1 - 0,16856 = 0,83144.
г) Найдем вероятность того, что вес случайно отобранной туши отклонится от математического ожидания меньше, чем на 50 кг, т.е.: P(½X - 950½< 50) =? Что значит: ½X - 950½< 50? Это неравенство можно заменить двойным неравенством: -50 < X - 950 < 50 или 950 - 50 < X < 950 + 50, 900 < X < 1000. Следовательно: P½X - 950½< 50) = Р(900 < Х < 1000). А это вероятность попадания в заданный интервал нормально распределенной случайной величины Х. Отсюда:
Согласно свойству функции Лапласа: -Ф0(-0,33) = Ф0(0,33). Найдем по таблице функции Лапласа (Приложение 2) значения Ф0(z). Ф0(0,33) = 0,1293. Следовательно: P(½X - 950½< 50) = Р(900 < Х < 1000) = 2 × 0,1293 = 0,2586. Вероятность того, что вес случайно отобранной туши отклонится от математического ожидания меньше, чем на 50 кг, составляет 0,2586. Эту задачу легче решить, используя формулу расчета вероятности заданного отклонения нормально распределенной случайной величины Х от своего математического ожидания:
где - D величина отклонения случайной величины Х от математического ожидания. По условию D = 50; а = 950, s = 150. Используя эту формулу, сразу получим: P(½X - 950½< 50) = 2Ф0(50 / 150) = 2Ф0(0,33) = 2 × 0,1293 = 0,2586. Проиллюстрируем решение задачи графически (рис. 5.4).
Рис.5.4. Графическая иллюстрация к задаче 5.1.
По условию данной задачи точка на оси абсцисс (z = -0,33) соответствует х = 900, т.е. весу, равному 900 кг, а точка (z = 0,33) соответствует х = 1000, т.е. весу, равному 1000 кг. Заштрихованная на графике площадь представляет собой вероятность того, что вес наудачу выбранной туши окажется в интервале от 900 до 1000 кг., т.е. отклонится от математического ожидания меньше, чем на 50 кг. д) Найдем вероятность того, что вес случайно отобранной туши отклонится от математического ожидания больше, чем на 50 кг, т.е.: P(½X - 950½> 50) =? Это вероятность события, противоположного по отношению к событию: вес случайно отобранной туши отклонится от математического ожидания меньше, чем на 50 кг (P(½X - 950½< 50)). Следовательно: P(½X - 950½> 50) = 1 - P(½X - 950½< 50) = 1 - 0,2586 = 0,7414. Вероятность того, что вес случайно отобранной туши отклонится от математического ожидания больше, чем на 50 кг, составляет 0,7414. Можно использовать другой алгоритм решения. Вероятность того, что вес случайно отобранной туши отклонится от математического ожидания больше, чем на 50 кг, - это вероятность того, что вес случайно отобранной туши будет или меньше (950 - 50 = 900) кг или больше (950 + 50 = 1000) кг. По теореме сложения вероятностей несовместных событий имеем: P(½X - 950½> 50) = P(X < 900) + P(X > 1000).
Отсюда: P(½X - 950½> 50) = P(X < 900) + P(X > 1000) = 0,3707 + 0,3707 = 0,7414.
е) Найдем границы, в которых отклонение веса случайно отобранной туши от своего математического ожидания не превысит утроенного среднего квадратического отклонения. В этом задании студентам предлагается проиллюстрировать правило трех сигм, которое можно сформулировать следующим образом: Если случайная величина распределена по нормальному закону, то ее отклонение от математического ожидания практически не превышает ±3s. Р(½Х - а ½<3s) = 2Ф0(3) = 0,9973. Вероятность того, что отклонение нормально распределенной случайной величины Х от своего математического ожидания будет меньше 3s или, другими словами, вероятность того, что нормально распределенная случайная величина Х попадет в интервал (а - 3s; а + 3s), равна 0,9973. Следовательно, вероятность того, что отклонение случайной величины от своего математического ожидания по абсолютной величине превысит утроенное среднее квадратическое отклонение, очень мала и равна 0,0027. Другими словами, лишь в 27 случаях из 10000 случайная величина Х в результате испытания может оказаться вне интервала (а - 3s; а + 3s). Такие события считаются практически невозможными. Формулу, описывающую правило трех сигм, несложно получить из формулы вероятности заданного отклонения нормально распределенной случайной величины Х от своего математического ожидания:
Если взять D = 3s, то получим D /s = 3. Отсюда: Р(½Х - а ½< 3s) = 2Ф0(3) = 0,9973.
По условию задачи: а = 950; s = 150. Правило трех сигм можно представить так: Р(а - 3s < Х < a + 3s) = 2Ф0(3) = 0,9973. Интересующие нас границы - это границы интервала (а - 3s; a + 3s), т.е.: а - 3s< Х < a + 3s, 950 – 3 × 150 < X < 950 + 3 × 150, 500 < X < 1400. Учитывая, что вес отобранной туши - нормально распределенная случайная величина, можно быть практически уверенным, что вес случайно отобранной туши не выйдет за пределы от 500 до 1400 кг.
ж) Определим границы, в которых с вероятностью 0,899 будет находиться вес случайно отобранной туши. Формулу вероятности заданного отклонения нормально распределенной случайной величины Х от своего математического ожидания можно представить следующим образом:
или
где g - вероятность того, что отклонение нормально распределенной случайной величины Х от своего математического ожидания не превысит заданной величины D. По условию задачи: а = 950; s = 150. Используя последнюю формулу, получим:
Из соотношения:
По таблице функции Лапласа (Приложение 2) найдем, при каком z = z = 1,64, т.е. Отсюда: D= 1,64 × 150 = 246. С вероятностью 0,899 можно ожидать, что отклонение веса случайно отобранной туши от своего математического ожидания не превысит 246 кг. Найдем границы интересующего нас интервала: а - D < Х < a + D, 950 - 246 < X < 950 + 246, 704 < X < 1196. С вероятностью 0,899 можно ожидать, что вес случайно отобранной туши будет находиться в пределах от 704 до 1196 кг. Ответ:а) 0,02275; б) 0,25143; в) 0,83144; г) 0,2586; д) 0,7414; е) (500; 1400); ж) 246; (704; 1196).
Пример 5.2. Изменим условие предыдущей задачи. На рынок поступила крупная партия говядины. Предполагается, что вес туш – случайная величина, подчиняющаяся нормальному закону распределения с неизвестным математическим ожиданием и средним квадратическим отклонением s =150 кг. Известно, что 37,07% туш имеют вес более 1000 кг. Определите ожидаемый вес случайно отобранной туши. Решение. По условию задачи: s = 150; a = 1000; b = +¥; P(X > 1000) = 0,3707. Ожидаемый вес случайно отобранной туши - это среднеожидаемый вес, математическое ожидание, т.е. а =? Используем формулу (5.10) расчета вероятности попадания в заданный интервал нормально распределенной случайной величины Х:
По таблице функции Лапласа (Приложение 2) найдем, при каком z = 0,33, т.е. Отсюда: 1000 - а = 0,33 × 150 = 50. а = 1000 - 50 = 950. Ответ. Среднеожидаемый вес случайно отобранной туши составляет 950 кг.
Пример 5.3. Вновь изменим условие задачи. На рынок поступила крупная партия говядины. Предполагается, что вес туш - случайная величина, подчиняющаяся нормальному закону распределения с математическим ожиданием а = 950 кг и неизвестным средним квадратическим отклонением. Известно, что 15,87% туш имеют вес менее 800 кг. Определите среднее квадратическое (стандартное) отклонение веса туш. Решение. По условию задачи: а = 950; a = -¥ b = 800; P(X < 800) = 0,1587; s =? Используем формулу (5.10) расчета вероятности попадания в заданный интервал нормально распределенной случайной величины Х:
По таблице функции Лапласа (Приложение 2) найдем, при каком z = 1, т.е. Отсюда: s= 150. Ответ. Среднее квадратическое отклонение веса туш составляет 150 кг.
Пример 5.4. В очередной раз изменим условие задачи. На рынок поступила крупная партия говядины. Предполагается, что вес туш - случайная величина, подчиняющаяся нормальному закону распределения с математическим ожиданием а = 950 кг и неизвестным средним квадратическим отклонением. Каким должно быть среднее квадратическое (стандартное) отклонение, чтобы с вероятностью 0,81648 можно было утверждать, что абсолютное отклонение веса случайно отобранной туши от математического ожидания не превысит 200 кг? Решение. По условию задачи: а = 950; D = 200; P(½X - 950½< 200) = 0,81648; s =? Используем формулу (5.11) расчета вероятности попадания заданного отклонения нормально распределенной случайной величины Х от своего математического ожидания:
Тогда получим: P(½X - 950½< 200) = 2Ф0(200 / s) = 0,81648; 2Ф0(200 / s = 0,81648; Ф0(200 / s) = 0,81648 / 2; Ф0(200 / s) = 0,40824. По таблице функции Лапласа (Приложение 2) найдем, при каком z = 1,33, т.е. Отсюда: s = 200 / 1,33 = 150. Ответ. Чтобы с вероятностью 0,81648 можно было утверждать, что абсолютное отклонение веса случайно отобранной туши от математического ожидания не превысит 200 кг, среднее квадратическое отклонение веса туш должно составлять 150 кг.
Пример 5.5 Фирма собирается приобрести партию из 100 000 единиц некоторого товара. Из прошлого опыта известно, что 1% товаров данного типа имеют дефекты. Какова вероятность того, что в данной партии окажется от 950 до 1050 дефектных единиц товара? Решение. В качестве случайной величины в данной задаче выступает число дефектных единиц товара в общей партии из 100000 единиц. Обозначим ее через X. Перечислим все возможные значения случайной величины Х: 0, 1, 2,..., 99999, 100000. Это - дискретная случайная величина, т.к. ее возможные значения отличаются друг от друга не менее чем на 1, и множество ее возможных значений является счетным. По условию вероятность того, что единица товара окажется дефектной, - постоянна и составляет 0,01 (p = 0,01). Вероятность противоположного события, т.е. того, что единица товара не имеет дефекта - также постоянна и составляет 0,99 (q = 1—p = 1—0,01 = 0,99). Все 100000 испытаний - независимы, т.е. вероятность того, что каждая единица товара окажется дефектной, не зависит от того, окажется дефектной или нет любая другая единица товара. Значения случайной величины Х - это, в общем виде, число появлений интересующего нас события в 100000 независимых испытаниях. Это позволяет сделать вывод о том, что случайная величина Х - число дефектных единиц товара в общей партии из 100000 единиц - подчиняется биномиальному закону распределения вероятностей с параметрами n = 100000 и p = 0,01. Итак, по условию задачи: n = 100000; p = 0,01; q = 0,99, X = m. Необходимо найти вероятность того, что число дефектных единиц товара окажется в пределах от m1 = 950 до m2 =1050, т.е. - вероятность того, что случайная величина X = m попадет в интервал от 950 до 1050, т.е.: P(m1 < m < m2) =? Так как мы имеем дело со случайной величиной, подчиняющейся биномиальному распределению, вероятность появления события m раз в n независимых испытаниях необходимо вычислять по формуле Бернулли (4.9).
В данном случае, для определения искомой вероятности нам необходимо с помощью формулы Бернулли найти P100000, 950; P100000, 951; P100000, 952;...; P100000, 1049; P100000, 1050, а затем - сложить их, используя теорему сложения вероятностей несовместных событий. Очевидно, что такой способ определения искомой вероятности связан с громоздкими вычислениями. Так, например:
Можно значительно облегчить расчеты, если аппроксимировать биномиальное распределение нормальным, т.е. выразить функции биномиального распределения через функции нормального. Когда n - число испытаний в биномиальном эксперименте - возрастает, дискретное биномиальное распределение стремится к непрерывному нормальному распределению. Это означает, что для больших n мы можем аппроксимировать биномиальные вероятности вероятностями, полученными для нормально распределенной случайной величины, имеющей такое же математическое ожидание и такое же среднее квадратическое отклонение. Подставим параметры биномиального распределения (5.15) в формулу (5.10) и получим формулу для приближенного расчета вероятности появления события от m1 и до m2 раз в n независимых испытаниях P(m1 < m > m2):
где Ф 0(z) - функция Лапласа:
Формулу для приближенного вероятности появления события не менее m1 и не более m2 раз в n независимых испытаниях Pn(m1 < m < m2) называют интегральной теоремой Лапласа. Использование локальной и интегральной теорем Лапласа дает приближенные значения искомых вероятностей. Погрешность будет невелика при условии, что npq > 9. Для решения данной задачи воспользуемся интегральной теоремой Лапласа:
По таблице функции Лапласа (Приложение 2) найдем Ф0(1,59): Ф0(1,59) = 0,44408.
Вероятность того, что в партии из 100000 единиц окажется от 950 до 1050 дефектных единиц товара, составляет 0,88816. Данную конкретную задачу можно было решить еще более просто. Математическое ожидание числа дефектных единиц товара равно 1000 единиц: M(m) = n × p = 100000 × 0,01 = 1000. Абсолютное отклонение нижней и верхней границ интервала [m1; m2] от математического ожидания M(m) = n × p составляет 50 единиц: ½m1 – n × p½=½950 – 100000 × 0,01½= 50; ½m2 - n × p½=½1050 – 100000 × 0,01½= 50. Следовательно, искомую вероятность можно рассматривать как вероятность заданного отклонения частоты от своего математического ожидания:
Подставив параметры биномиального распределения в формулу расчета вероятности заданного отклонения нормально распределенной случайной величины от своего математического ожидания, получим формулу для приближенного расчета вероятности заданного отклонения частоты от своего математического ожидания:
При использовании этой формулы для решения задачи сразу получим:
Ответ. Вероятность того, что в партии из 100000 единиц окажется от 950 до 1050 дефектных единиц товара, составляет 0,88816.
Пример 5.6. Фирма собирается приобрести партию из 100 000 единиц некоторого товара. Из прошлого опыта известно, что 1% товаров данного типа имеют дефекты. Какова вероятность того, что в данной партии окажется 1020 дефектных единиц товара? Решение. Так как
Найдем Найдем
Ответ. Вероятность того, что в партии из 100000 единиц окажется 1020 дефектных единиц товара, составляет 0,0103.
Пример 5.7. Подлежат исследованию 400 проб руды. Вероятность промышленного содержания металла в каждой пробе для всех проб одинакова и равна 0,8. Найти вероятность того, что доля проб с промышленным содержанием металла отклонится от вероятности промышленного содержания металла в каждой пробе не более чем на 0,05. Решение. В отличие от предыдущей задачи, в данном случае речь идет о расчете вероятности заданного отклонения частости (относительной частоты) появления события от вероятности его появления в отдельном независимом испытании, т.е.:
При возрастании числа независимых испытаний распределение частости стремится к нормальному распределению точно так же, как и распределение частоты. Это означает, что при больших n мы можем аппроксимировать распределение частости нормальным распределением случайной величины, имеющей такое же математическое ожидание и такое же среднее квадратическое отклонение. Подставив параметры распределения частости в формулу расчета вероятности заданного отклонения нормально распределенной случайной величины от своего математического ожидания, получим формулу для приближенного расчета вероятности заданного отклонения частости от своего математического ожидания (вероятности): Параметры распределения частости:
Используя эти формулы, получим:
Применим данную формулу для решения задачи. По условию: n = 400; p = 0,8; q = 1- 0,8 = 0,2; D = 0,05.
Ответ. Вероятность того, что доля проб с промышленным содержанием металла отклонится от вероятности промышленного содержания металла в каждой пробе не более чем на 0,05, составляет 0,98758.
Задачи к теме 5
1. Компьютерная система содержит 50 одинаковых микрочипов. Вероятность того, что любой микрочип будет работать в заданное время, равна 0,9. Для выполнения некоторой операции требуется, чтобы, по крайней мере, 30 микрочипов было в рабочем состоянии. а) Чему равна вероятность того, что операция будет выполнена успешно? б) Чему равна вероятность того, что будут работать 47 микрочипов? 2. Почтовое отделение быстро оценивает объём переводов в рублях, взвешивая почтовые отправления, полученные в течение каждого текущего рабочего дня. Установлено, что если вес почтовых отправлений составляет N кг, то объём переводов в рублях есть случайная величина, распределенная по нормальному закону со средним значением 160N и стандартным отклонением 20N руб. Найти вероятность того, что в день, когда вес почтовых отправлений составит 150 кг, объём переводов в рублях будет находиться в пределах: а) от 21000 до 27000 руб.; б) более 28500 руб.; в) менее 22000 руб. 3.Менеджер крупного ресторана по опыту знает, что только 80% людей, сделавших заказ на вечер, придут в ресторан поужинать. В один из вечеров менеджер решил принять 60 заказов, хотя в ресторане было лишь 55 свободных столиков. Чему равна вероятность того, что более 55 посетителей придут на заказанные места?
4. Экзамен по математической статистике успешно сдают 75% студентов дневного отделения. Если на втором курсе факультета обучается 250 студентов, то какова вероятность того, что 203 студента сдадут экзамен успешно? 5. В отделе продаж страховой компании работают 45 сотрудников. Вероятность того, что сотрудник выполнит план по числу заключенных договоров, оценивается начальником отдела как 0,7. Какова вероятность того, что: а) план выполнят как минимум 35 сотрудников? б) план выполнят не более 30 сотрудников? в) план выполнят 37 сотрудников?
6. Отдел маркетинга фармацевтической компании утверждает, что новая модификация таблеток от головной боли используется 30% пациентов. Если среди пациентов было отобрано 80 человек, то какова вероятность того, что отобранная доля лиц, предпочитающих новую модификацию таблеток, не будет отличаться по абсолютной величине от истинной доли более чем на 0,1? 7. Дневная выручка супермаркета распределена по нормальному закону с математическим ожиданием 10000 у.е. и стандартным отклонением 1400 у.е. Найдите вероятность того, что: а) выручка супермаркета окажется более 13000 у.е.; б) выручка супермаркета окажется менее 8000 у.е.; в) найдите границы, в которых будет находиться выручка супермаркета согласно правилу трех сигм.
8. По данным независимого исследования, хлеб определенного сорта, составляет 15% от совокупной реализации хлебобулочных изделий. Если выборочному обследованию были подвергнуты 80 торговых предприятий, то какова вероятность того, что доля реализации хлеба определенного сорта в генеральной совокупности будет отличаться по абсолютной величине от истинной доли менее чем на 5%?
9. В течение месяца кредитным отделом банка было выдано 68 ипотечных кредитов. Менеджер банка оценивает вероятность просрочки оплаты таких кредитов как 0,2. Какова вероятность того, что в течени
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1061; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.014 с.) |

 :
: (5.1)
(5.1) до
до  равна приращению функции распределения на концах этого промежутка:
равна приращению функции распределения на концах этого промежутка: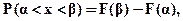 (5.2),
(5.2), , когда F(X) - непрерывна в точке
, когда F(X) - непрерывна в точке  =
= 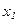
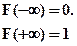 (5.3)
(5.3) (x). (5.4)
(x). (5.4)
 до +
до +  (5.5)
(5.5) до
до  может быть вычислена по формуле:
может быть вычислена по формуле: (5.6)
(5.6)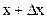 , где
, где  бесконечно малая величина.
бесконечно малая величина. (5.7)
(5.7)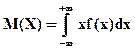 (5.8),
(5.8), (5.9)
(5.9) (5.10)
(5.10) . Вероятностный смысл параметров:
. Вероятностный смысл параметров:  =М(X), а
=М(X), а  . Обозначение:
. Обозначение:
 (5.11)
(5.11) (интеграл Лапласа)
(интеграл Лапласа) обладает свойствами:
обладает свойствами:
 (см. таблицу приложения 2).
(см. таблицу приложения 2). имеем:
имеем: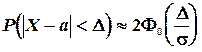 (5.12)
(5.12)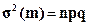 (5.13)
(5.13)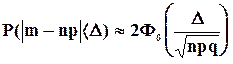 (5.14)
(5.14) с числовыми характеристиками
с числовыми характеристиками 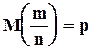 и
и 
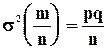
 (5.16)
(5.16)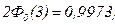 нормально распределенная случайная величина Х удовлетворяет неравенству:
нормально распределенная случайная величина Х удовлетворяет неравенству: (5.17)
(5.17) .
. и p
и p  1 и достаточно большом n биноминальное распределение близко к нормальному закону (причем их математические ожидания и дисперсии совпадают), т.е. имеет место равенство:
1 и достаточно большом n биноминальное распределение близко к нормальному закону (причем их математические ожидания и дисперсии совпадают), т.е. имеет место равенство: , где
, где 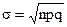 , a =nр
, a =nр (5.18)
(5.18) (х) - плотность вероятностей стандартной нормальной случайной величины
(х) - плотность вероятностей стандартной нормальной случайной величины  и
и 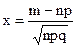 ).
).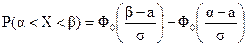 ,
,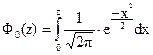


 .
.
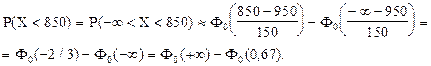














 , найдем D.
, найдем D.

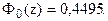
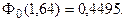

 ;
;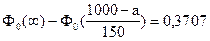 ;
; ;
; .
.



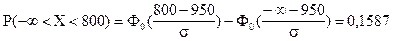 ;
; ;
; ;
; ;
; .
.


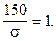




 .
. ,
, , (5.19)
, (5.19) .
. ;
; ;
; ;
; ;
; .
.


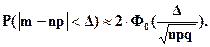 (5.20)
(5.20) ;
;
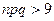 , применим локальную теоремуМуавра-Лапласа:
, применим локальную теоремуМуавра-Лапласа:
 .
.

 ;
;  ;
;  .
.
 (5.21)
(5.21) ;
;



