
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выборочный метод и статистическое оцениваниеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
7.1. Основные понятия и определения выборочного метода Одно из популярных определений статистики говорит, что это – наука, позволяющая распространять выводы, сделанные на основе изучения части совокупности (случайной выборки), на всю совокупность (генеральную совокупность). В этом определении заключена сущность выборочного метода и его ведущая роль в статистике. Все единицы совокупности, обладающие интересующими исследователя признаками, составляют генеральную совокупность. Часть совокупности, случайным образом отобранная из генеральной совокупности – выборочная совокупность – выборка.[2] Число единиц (элементов) статистической совокупности называется её объёмом. Объем генеральной совокупности обозначается N, а объем выборочной совокупности n. Если объем совокупности велик, то его полагают равным бесконечности. Случайная выборка из n элементов - это такой отбор, при котором элементы извлекаются по одному из всей генеральной совокупности и каждый из них имеет равный шанс быть отобранным. Требование случайности обеспечивается отбором по таблицам случайных чисел или по жребию. Такая выборка называется собственно-случайной. Одним из примеров использования собственно-случайной выборки является проведение тиражей выигрышей денежно-вещевых лотерей, при которых обеспечивается равная возможность попадания в тираж любого номера лотерейного билета. По способу отбора элементов различают два типа случайных выборок: собственно-случайная повторная выборка (схема возвращенного шара); собственно-случайнаябесповторная выборка (схема невозвращенного шара). Выбор схемы отбора зависит от характера изучаемого объекта. Напомним, что при повторном отборе единица наблюдения после извлечения из генеральной совокупности регистрируется и вновь возвращается в генеральную совокупность, откуда опять может быть извлечена случайным образом. При бесповторном отборе отобранный элемент в выборку обратно не возвращается. Необходимо заметить, что независимо от способа организации выборки она должна представлять собой уменьшенную копию генеральной совокупности, то есть быть представительной (репрезентативной). Статистическое оценивание
Пусть из генеральной совокупности извлекается выборка объема n, причем значение признака х1 наблюдается m1 раз, х2 m2 раз,..., хk наблюдается mk раз, Мы можем сопоставить каждому значению xi относительную частоту mi/n. Статистическим распределением выборки называют перечень возможных значений признака xi и соответствующих ему частот или относительных частот (частостей) mi (wi). Числовые характеристики генеральной совокупности, как правило неизвестные, (средняя, дисперсия и др.) называют параметрами генеральной совокупности (обозначают, например, По данным выборки рассчитывают числовые характеристики, которые называют статистиками (обозначают В качестве точечных оценок параметров генеральной совокупности используются соответствующие выборочные характеристики. Теоретическое обоснование возможности использования этих выборочных оценок для суждений о характеристиках и свойствах генеральной совокупности дают закон больших чисел и центральная предельная теорема Ляпунова. Выборочная средняя является точечной оценкой генеральной средней, т.е. Генеральная дисперсия имеет 2 точечные оценки: -
При больших объемах выборки Генеральное среднее квадратическое отклонение Ошибки выборки
Поскольку выборочная совокупность представляет собой лишь часть генеральной совокупности, то вполне естественно, что выборочные характеристики не будут точно совпадать с соответствующими генеральными. Ошибка репрезентативности может быть представлена как разность между генеральными и выборочными характеристиками изучаемой совокупности: Применительно к выборочному методу из теоремы Чебышева следует, что с вероятностью сколь угодно близкой к единице можно утверждать, что при достаточно большом объеме выборки и ограниченной дисперсии генеральной совокупности разность между выборочной средней и генеральной средней будет сколь угодно мала.
где
Запись показывает, что о величине расхождения между параметром и статистикой Формула (7.2) устанавливает связь между пределом ошибки Cогласно центральной предельной теореме Ляпунова выборочные распределения статистик (при n ³ 30) будут иметь нормальное распределение независимо от того, какое распределение имеет генеральная совокупность. Следовательно:
где Ф0(t) - функция Лапласа.
Значения вероятностей, соответствующие различным t, содержатся в специальных таблицах: при n ³ 30 - в таблице значений Ф0(t), а при n < 30 в таблице распределения t -Стьюдента. Неизвестное значение В зависимости от способа отбора средняя ошибка выборки определяется по разному: Таблица 7.1
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 502; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.126.199 (0.007 с.) |

 - объем выборки.
- объем выборки.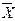 или
или  ,
,  ). Доля единиц, обладающих тем или иным признаком в генеральной совокупности, называется генеральной долей и обозначается р.
). Доля единиц, обладающих тем или иным признаком в генеральной совокупности, называется генеральной долей и обозначается р. , или
, или  ,
,  , выборочная доля обозначается w). Статистики, получаемые по различным выборкам, как правило, отличаются друг от друга. Поэтому статистика, полученная из выборки, является только оценкой неизвестного параметра генеральной совокупности. Оценка параметра - определенная числовая характеристика, полученная из выборки. Когда оценка определяется одним числом, ее называют точечной оценкой.
, выборочная доля обозначается w). Статистики, получаемые по различным выборкам, как правило, отличаются друг от друга. Поэтому статистика, полученная из выборки, является только оценкой неизвестного параметра генеральной совокупности. Оценка параметра - определенная числовая характеристика, полученная из выборки. Когда оценка определяется одним числом, ее называют точечной оценкой.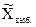 ≈
≈ 
 выборочная дисперсия;
выборочная дисперсия;  - исправленная выборочная дисперсия[3]. -
- исправленная выборочная дисперсия[3]. -  , а
, а  . Причем в математической статистике доказывается, что
. Причем в математической статистике доказывается, что или
или  (7.1)
(7.1) так же имеет 2 точечные оценки:
так же имеет 2 точечные оценки:  - выборочное среднее квадратическое отклонение и
- выборочное среднее квадратическое отклонение и  - исправленное выборочное среднее квадратическое отклонение.
- исправленное выборочное среднее квадратическое отклонение. 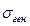 при
при  , а
, а  для оценивания
для оценивания  ;при этом
;при этом  , а
, а  .
. , либо
, либо  .
. (7.2)
(7.2) - средняя по генеральной совокупности,
- средняя по генеральной совокупности, - среднее квадратическое отклонение в генеральной совокупности.
- среднее квадратическое отклонение в генеральной совокупности. , можно судить лишь с определенной вероятностью, от которой зависит величина t.
, можно судить лишь с определенной вероятностью, от которой зависит величина t. , гарантируемым с некоторой вероятностью Р, величиной tи средней ошибкой выборки
, гарантируемым с некоторой вероятностью Р, величиной tи средней ошибкой выборки  .
. (7.3)
(7.3)



