
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Герасимова И.А., Житников И.В., Федосова О.Н.Содержание книги
Поиск на нашем сайте
Практикум по теории вероятностей и математической статистике УДК 311(075.8) ББК 606я73 Н60
Рецензенты: Ниворожкина Л. И., Морозова З. А., Герасимова И. А., Житников И. В., Федосова О.Н. Н60 Практикум по теории вероятностей и математической статистике: Учебное пособие. – Ростов н/Д: РГЭУ, 2007.
ISBN 5-222-00560-7
В пособии кратко и просто изложены основные понятия статистики и теории вероятностей, даны методические указания по решению типовых задач. В конце каждой главы приведены 20 вариантов задач, условия которых приближены к практическим ситуациям в области маркетинга, аудита, финансов и др. Предназначены для студентов и аспирантов экономических вузов, преподавателей колледжей, вузов, а также для практических работников, желающих научиться использовать современные статистические методы и их практические приложения при планировании своей деятельности.
УДК 311(075.8) ББК 60я73 ISBN 5-222-00560-7 Ниворожкина Л.И.,Морозова З.А., Герасимова И. А., Житников И. В., Федосова О.Н.
ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ С ЭЛЕМЕНТАМИ ТЕОРИИ ВЕРОЯТНОСТЕЙ
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
1. Предмет и основные определения теории вероятностей. 2. Классическое определение вероятности. Свойства вероятности, вытекающие из классического определения. Примеры. 3. Статистическое определение вероятности, его особенности и связь с классическим определением. 4. Полная группа несовместных событий, противоположные события, свойства их вероятностей. 5. Зависимые и независимые события. Условные и безусловные вероятности. 6. Теоремы умножения вероятностей. 7. Теоремы сложения вероятностей. 8. Формула полной вероятности. Формула Байеса. 9. Комбинаторика: размещения, сочетания, перестановки. Размещения, сочетания и перестановки с повторениями. Примеры. 10. Случайные величины и случайные события. Дискретные и непрерывные случайные величины. Закон распределения случайной величины и способы его задания. 11 Числовые характеристики случайных величин. Начальные и центральные моменты. Асимметрия и эксцесс. 12 Математическое ожидание случайной величины. Его смысл и примеры. Свойства математического ожидания. 13. Дисперсия и среднее квадратическое отклонение случайной величины. Их смысл и примеры вычисления. Формулы для вычисления дисперсии. Свойства дисперсии. 14. Математическое ожидание, дисперсия и среднее квадратическое отклонение частоты и частости. 15.Формула Бернулли. Биномиальное распределение. Наивероятнейшее число появлений события. 16.Формула Пуассона. Закон распределения вероятностей редких событий. 17. Гипергеометрическое распределение. 18. Равномерное распределение. 19.Непрерывные случайные величины. Дифференциальная и интегральная функции их распределения, их смысл и связь между ними. 20. Вероятность попадания случайной величины в заданный интервал. Вероятность того, что непрерывная случайная величина примет точно заданное значение. 21. Нормальное распределение. Плотность нормального распределения и ее свойства. Функция распределения нормально распределенной случайной величины. 22. Нормированное (стандартное) нормальное распределение. 23. Функция Лапласа: график, свойства, таблицы. 24. Вероятность попадания нормально распределенной случайной величины в заданный интервал. 25.Вероятность заданного отклонения нормальной случайной величины от своего математического ожидания. Правило трех сигм. 26. Локальная теорема Лапласа. 27. Интегральная теорема Лапласа. 28. Закон больших чисел. Понятие о теореме Чебышева (общий случай). Значение теоремы Чебышева. 29. Закон больших чисел. Теорема Бернулли. 30. Понятие о центральной предельной теореме Ляпунова. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
31. Предмет и основные задачи математической статистики. 32. Вариационные ряды. Виды вариации. Границы интервалов в вариационных рядах, величина интервала. Накопленные частоты. 33. Графическое изображение вариационных рядов. 34. Числовые характеристики вариационного ряда. Средняя арифметическая и ее свойства, мода и медиана. 35.Показатели колеблемости: вариационный размах, дисперсия, стандартное отклонение, коэффициент вариации. 36. Моменты вариационного ряда (начальные и центральные). 37. Дихотомическая вариация. Дисперсия альтернативного признака. 38.Основные положения теории выборочного метода. Генеральная совокупность и выборка. 39. Повторная и бесповторная собственно- случайная выборка. 40 Ошибки регистрации и ошибки репрезентативности. Предельная ошибка выборки. 41. Средняя ошибка выборки (для средней и для доли). 42. Необходимая численность выборки. Определение объема выборки при различных способах отбора. 43. Малые выборки. 44. Законы распределения, применяемые в математической статистике: распределения Стьюдента, Пирсона, Фишера. 45.Статистические оценки параметров распределения (сущность теории оценивания): несмещенность, состоятельность, эффективность оценок. 46. Точечные оценки: выборочная средняя, дисперсия, среднее квадратическое отклонение. 47. Точечная оценка генеральной средней по выборочной средней. 48. Точечная оценка генеральной дисперсии. “Исправленные” выборочная дисперсия и среднее квадратическое отклонение. 49. Интервальные оценки. Точность оценки. Доверительная вероятность. 50. Доверительные интервалы для оценки неизвестного значения генеральной средней и генеральной доли. 51.Статистическая проверка гипотез. Статистическая гипотеза: параметрическая и непараметрическая; нулевая и альтернативная. Ошибки I и II рода. Уровень значимости и мощность критерия. 52. Статистический критерий проверки нулевой гипотезы. Наблюдаемое значение критерия. Критическая область. Область принятия гипотезы. Критические точки. Отыскание односторонней и двусторонней критических областей. 53. Основные этапы проверки статистических гипотез. 54. Проверка гипотезы о равенстве двух дисперсий нормально распределенных генеральных совокупностей. 55. Проверка гипотезы о равенстве двух средних произвольно распределенных генеральных совокупностей (большие независимые выборки). 56. Проверка гипотезы о равенстве двух средних нормально распределенных генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки). 57. Проверка гипотезы о равенстве выборочной средней и гипотетической генеральной средней нормальной совокупности при известной и неизвестной генеральной дисперсии. 58. Проверка гипотезы о равенстве наблюдаемой относительной частоты и гипотетической вероятности появления события. 59. Проверка гипотезы о равенстве долей признака в двух совокупностях. 60. Проверка гипотезы о законе распределения случайной величины. Критерий согласия Пирсона.
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ ДОМАШНЕГО ЗАДАНИЯ (КОНТРОЛЬНОЙ РАБОТЫ)
При выполнении домашнего задания (контрольной работы) следует строго придерживаться следующих правил:
Ростовский государственный экономический университет «РИНХ»
Кафедра математической статистики, эконометрики и актуарных расчетов
Домашнее задание по математической статистике с элементами теории вероятностей
Вариант №
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ Для успешного решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики. Комбинаторика происходит от латинского слова ”combinatio” соединение. Группы, составленные из каких-либо предметов, (безразлично каких, например, букв, цветных шаров, кубиков, чисел и т.п.), называются соединениями (комбинациями). Предметы, из которых состоят соединения, называются элементами. Различают три типа соединений: перестановки, размещения и сочетания.
Размещения Размещениями из n элементов по m в каждом называются такие соединения, каждое из которых содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга либо самими элементами (хотя бы одним), либо лишь порядком их расположения. Число размещений из n элементов по m в каждом обычно обозначается символом
Понятие факториала Произведение n натуральных чисел от 1 до n обозначается сокращенно n!, то есть Например, Считается, что 0! = 1. Используя понятие факториала, формулу (1.1) можно представить так:
где Очевидно, что Пример 1.1. Правление коммерческого банка выбирает из 10 кандидатов трех человек на различные должности (все 10 кандидатов имеют равные шансы). Сколько всевозможных групп состоящих из трех человек, можно составить из 10 кандидатов? Решение. В условии задачи речь идет о расчете числа комбинаций из 10 элементов по 3. Так как группы по 3 человека могут отличаться и составом претендентов, и заполняемыми ими вакансиями, т.е. порядком, то для ответа на пункт а) необходимо рассчитать число размещений из 10 элементов по 3.
Ответ. Из 10 человек можно составить 720 различных групп, состоящих из трех человек.
Размещения с повторениями
Размещение с повторениями из n элементов по m(m × n) элементов может содержать любой элемент сколько угодно раз от 1 до m включительно, или не содержать его совсем, то есть каждое размещение с повторениями из n элементов по m элементов может состоять не только из различных элементов, но из m каких угодно и как угодно повторяющихся элементов. Соединения, отличающиеся друг от друга хотя бы порядком расположения элементов, считаются различными размещениями. Число размещений с повторениями из n элементов по m элементов будем обозначать символом Можно доказать, что оно равно nm.
Пример 1.2. Изменим условиепримера 1.1. Правление коммерческого банка выбирает из 10 кандидатов трех человек на три различные должности, Предположим, что один и тот же отобранный из 10 претендентов кандидат, может занять не только одну, но и 2, и даже все 3 различные вакантные должности. Сколько в этом случае возможно комбинаций замещения трех вакантных должностей? Решение. Как и в предыдущей задаче комбинации замещения вакантных должностей могут отличаться и составом претендентов, и заполняемыми ими вакансиями, т.е. порядком. Следовательно, и в этом случае для ответа на вопрос задачи необходимо рассчитать число размещений. Однако, на этот раз, вакантные должности могут замещаться одним и тем же претендентом, а, значит, здесь речь идет о расчете числа размещений с повторениями. По условию задачи n = 10, m = 3. Следовательно:
Ответ. Можно составить 1000 комбинаций замещения 3 различных вакантных должностей.
Сочетания Сочетаниями из n элементов по m в каждом называются такие соединения, каждое из которых содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга по крайней мере одним элементом. Число сочетаний из n элементов по m в каждом обозначается символом
или
Пример 1.3. Правление коммерческого банка выбирает из 10 кандидатов трех человек на одинаковые должности (все 10 кандидатов имеют равные шансы). Сколько всевозможных групп по три человека можно составить из 10 кандидатов? Решение. Состав различных групп должен отличаться, по крайней мере, хотя бы одним кандидатом и порядок выбора кандидата не имеет значения, следовательно, этот вид соединений представляет собой сочетания. По условию задачи n = 10? M = 3. Подставив данные в формулу (1.4.2), получаем
Ответ. Можно составить 120 групп из 10 человек по 3. Замечание. Надо уметь отличать сочетания от размещений. Если, например, в группе 25 студентов, и 10 человек из них вышли из аудитории на перерыв. Они стоят вместе и беседуют. Тогда порядок, в котором они стоят - несущественен. Число всех возможных групп из 25 человек по 10 в этом случае - сочетания. Если же студенты отправились на перерыве в буфет, или в кассу за стипендией, то тогда существенно, в каком порядкеонивстали, то есть кто из них первый, второй и т.д. В этой ситуации при подсчете возможных групп из 25 человек по 10 необходимо составлять размещения.
Сочетания с повторениями Сочетание с повторениями из n элементов по m(m Î n) элементов может содержать любой элемент сколько угодно раз от 1 до m включительно, или не содержать его совсем, то есть каждое сочетание из n элементов по m элементов может состоять не только из m различных элементов, но из m каких угодно и как угодно повторяющихся элементов. Следует отметить, что если, например, два соединения по m элементов отличаются друг от друга только порядком расположения элементов, то они не считаются различными сочетаниями. Число сочетаний с повторениями из n элементов по m будем обозначать символом
Замечание: m может быть и больше n. Пример 1.4. Сколькими способами можно выбрать 6 пирожных в кондитерской, где есть 4 разных сорта пирожных? Решение.
гдеm>n. Ответ. Существует 84 различных способа выбора пирожных. Перестановки
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 307; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.253.84 (0.008 с.) |

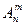 и вычисляется по формуле (1.1)[1]:
и вычисляется по формуле (1.1)[1]: .
.
 (читается: n факториал).
(читается: n факториал). .
. ,
,
 .
. = n (при m=1) и
= n (при m=1) и  = 1 (при m=0).
= 1 (при m=0). .
.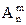 (c повт.)
(c повт.)
 (с повт.) = 103 = 1000.
(с повт.) = 103 = 1000.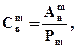 где
где  ,
,
 где
где 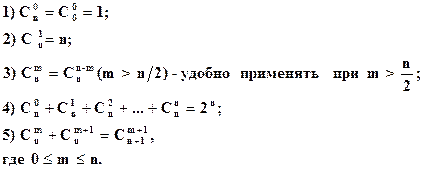
 = 10!/3!7! = 120
= 10!/3!7! = 120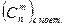 Формула для вычисления числа сочетаний с повторениями:
Формула для вычисления числа сочетаний с повторениями:
 ,
,


