
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы расчёта ошибки выборки для собственно-случайного отбораСодержание книги
Поиск на нашем сайте
Здесь
7.4. Определение численности (объема) выборки Одной из важнейших проблем выборочного метода является определение необходимого объема выборки. От объема выборки зависит размер средней ошибки Из формулы предельной ошибки Таблица 7.2 Формулы расчёта необходимой численности выборки Для собственно-случайного отбора
Интервальное оценивание Мы уже знаем, что
Мы получили интервальную оценку генеральной средней. Из теоремы Чебышева следует, что
Интервальной оценкой называют оценку, которая определяется двумя числами - концами интервала, который с определенной вероятностью накрывает неизвестный параметр генеральной совокупности. Интервал, содержащий оцениваемый параметр генеральной совокупности, называют доверительным интервалом. Для его определения вычисляется предельная ошибка выборки Предельная ошибка выборки равна t-кратному числу средних ошибок выборки. Коэффициент t позволяет установить, насколько надежно высказывание о том, что заданный интервал содержит параметр генеральной совокупности. Если мы выберем коэффициент таким, что высказывание в 95% случаев окажется правильным и только в 5% - неправильным, то мы говорим: со статистической надежностью в 95% доверительный интервал выборочной статистики содержит параметр генеральной совокупности. Статистической надежности в 95% соответствует доверительная вероятность - 0,95. В 5% случаев утверждение "параметр принадлежит доверительному интервалу" будет неверным. То есть 5% задает уровень значимости ( С помощью доверительного интервала можно оценить не только генеральную среднюю, но и другие неизвестные параметры генеральной совокупности. Для оценки математического ожидания а (генеральной средней ) [5]нормально распределенного количественного признака Х по выборочной средней
где t определяется по таблицам функции Лапласа из соотношения 2F0(t) = g;
n - объем выборки (число обследованных единиц). D определяется по формуле:
Для оценки математического ожидания а (генеральной средней ) нормально распределенного количественного признака Х по выборочной средней
D определяется по формуле:
Для оценки математического ожидания а (генеральной средней) нормально распределенного количественного признака Х по выборочной средней
где t определяется по таблицам Стьюдента по уровню значимости a = 1 - g и числу степеней свободы k = n - 1; s - исправленное выборочное среднее квадратическое отклонение; n - объем выборки. D определяется по формуле:
Для оценки математического ожидания а (генеральной средней) нормально распределенного количественного признака Х по выборочной средней
D определяется по формуле:
Для оценки генеральной доли р нормально распределенного количественного признака по выборочной доле
где t определяется по таблицам функции Лапласа из соотношения 2F0(t) = g; w - выборочная доля; n - объем выборки (число обследованных единиц). D определяется по формуле:
Для оценки генеральной доли р нормально распределенного количественного признака по выборочной доле
D определяется по формуле:
Для оценки генеральной доли р нормально распределенного количественного признака по выборочной доле
где t определяется по таблицам Стьюдента по уровню значимости a = 1 - g и числу степеней свободы k = n - 1. D определяется по формуле:
Для оценки генеральной доли р нормально распределенного количественного признака по выборочной доле
D определяется по формуле:
Пример 7.1. С помощью собственно-случайного повторного отбора руководство фирмы провело выборочное обследование 900 своих служащих. Средний стаж их работы в фирме равен 8,7 года, а среднее квадратическое (стандартное) отклонение - 2,7 года. Среди обследованных оказалось 270 женщин. Считая стаж работы служащих фирмы распределённым по нормальному закону, определите: а) с вероятностью 0,95 доверительный интервал, в котором окажется средний стаж работы всех служащих фирмы; б) с вероятностью 0,90 доверительный интервал, накрывающий неизвестную долю женщин во всем коллективе фирмы. Решение. По условию задачи выборочное обследование проведено с помощью собственно-случайного повторного отбора. Объем выборки n = 900 единиц, т.е. выборка - большая. а) Найдем границы доверительного интервала среднего стажа работы всего коллектива фирмы, т.е. границы доверительного интервала для генеральной средней. По условию: Используем формулу:
Найдем t из соотношения 2F0(t) = g: 2F0(t) = 0,95; аса (приложение 2) найдем, при каком t F0(t) = 0,475. F0(1,96) F0(t) = 0,95 / 2 = 0,475; По таблице функции Лапл = 0,475. Следовательно, t = 1,96. Найдем предельную ошибку выборки:
С вероятностью 0,95 можно ожидать, что средний стаж работы всего коллектива фирмы находится в интервале от 8,5236 до 8,8764 года.
б) Теперь оценим истинное значение доли женщин во всем коллективе фирмы. По условию: m = 270; n = 900; g = 0,9. Выборочная доля Рассмотрим формулу:
Найдем t из соотношения 2F0(t) = g: 2F0(t) = 0,9; F0(t) = 0,9 / 2 = 0,45. По таблице функции Лапласа (приложение 2) определим при каком t F0(t) = 0,45. F0(1,64) = 0,45. Следовательно, t = 1,64. Предельная ошибка выборки определяется по формуле:
Итак, с вероятностью 0,9 можно ожидать, что доля женщин во всем коллективе фирмы находится в интервале от 0,2749 до 0,3251. Ответ. Можно ожидать, что с вероятностью 0,95, средний стаж работы всех служащих фирмы находится в интервале от 8,5236 до 8,8764 года. С вероятностью 0,90 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0,2749 до 0,3251. Пример 7.2 Изменим условие примера 7.1. а) С помощью собственно-случайного повторного отбора определяется средний стаж работы служащих фирмы. Предполагается, что он подчиняется нормальному закону. Каким должен быть объем выборки, чтобы с доверительной вероятностью 0,95 можно было утверждать, что принимая полученный средний стаж работы за истинный, совершается погрешность, не превышающая 0,5 года, если стандартное отклонение s равно 2,7 года? б) Каким должен быть объем собственно-случайной повторной выборки, чтобы с надежностью 0,90 можно было утверждать, что максимальное отклонение выборочной доли женщин в выборке от доли женщин во всем коллективе фирмы не превышало 0,05, если в прошлом аналогичном обследовании выборочная доля женщин оказалась равной 0,3? Решение. В данной задаче нужно найти необходимую численность выборки. Расчет необходимой численности выборки дает ответ на вопрос: “Сколько нужно обследовать единиц совокупности, чтобы с заранее заданной вероятностью не превысить заранее заданную ошибку?” а) Дано: D = 0,5; s = 2,7; g = 0,95. По условию задачи требуется найти необходимую численность выборки для средней при повторном отборе. Воспользуемся формулой расчета необходимой численности выборки для средней для собственно-случайного повторного отбора:
Неизвестное значение t найдем из соотношения 2F0(t) = g: 2F0(t) = 0,95; F0(t) = 0,95 / 2 = 0,475; По таблице функции Лапласа (приложение 2) найдем при каком t F0(t) = 0,475. F0(1,96) = 0,475. Следовательно, t = 1,96. Рассчитаем необходимую численность выборки:
Так как n - целое число, а также, учитывая необходимость не превысить заданную ошибку, округлим полученный результат до большего целого. Следовательно, необходимо обследовать не менее 113 служащих. Ответ. Чтобы с вероятностью 0,95 и D= 0,5 года с помощью собственно-случайного повторного отбора определить средний стаж работы в фирме, необходимо обследовать не менее 113 служащих.
б) Дано: D = 0,05; w = 0,3; g = 0,9. По условию задачи требуется найти необходимую численность выборки для доли для собственно-случайного повторного отбора. Воспользуемся формулой расчета необходимой численности выборки для доли для собственно-случайного повторного отбора:
Найдем t из соотношения 2F0(t) = g: 2F0(t) = 0,9; F0(t) = 0,9 / 2 = 0,45. По таблице функции Лапласа (приложение 2) найдем при каком t F0(t) = 0,45. F0(1,64) = 0,45. Следовательно, t = 1,64. Рассчитаем необходимую численность выборки:
Так как n - целое число, а также, учитывая необходимость не превысить заданную ошибку, округлим полученный результат до большего целого. Следовательно, n» 226. Ответ. Чтобы с вероятностью 0,9 и ошибкой
Пример 7.3 Владелец автостоянки опасается обмана со стороны своих служащих (охраны автостоянки). В течение года (365 дней) владельцем автостоянки проведено 40 проверок. По данным проверок среднее число автомобилей, оставляемых на ночь на охрану, составило 400 единиц, а среднее квадратическое (стандартное) отклонение их числа - 10 автомобилей. а) Считая отбор собственно-случайным, с вероятностью 0,99 оцените с помощью доверительного интервала истинное среднее число автомобилей, оставляемых на ночь на охрану. Обоснованны ли опасения владельца автостоянки, если по отчетности охранников среднее число автомобилей, оставляемых на ночь на стоянку, составляет 395 автомобилей? Решение. По условию задачи выборочное обследование проведено с помощью собственно-случайного отбора. Очевидно, что отбор - бесповторный, т.к. не имеет смысла производить проверку более 1 раза в сутки. Объем выборки n = 40, что больше 30 единиц, т.е. выборка - большая. Объём генеральной совокупности N==365. а) Найдем границы доверительного интервала для оценки среднего числа автомобилей, оставляемых на ночь на охрану, т.е. границы доверительного интервала для генеральной средней. По условию: Используем формулу:
Найдем t из соотношения 2F0(t) = g: 2F0(t) = 0,99; F0(t) = 0,99 / 2 = 0,495; По таблице функции Лапласа (приложение 2) найдем при каком t F0(t) = 0,495. F0(2,58) = 0,495. Следовательно, t = 2,58. Найдем предельную ошибку выборки:
Ответ. С уверенностью в 99% можно ожидать, что среднее число автомобилей, оставляемых на ночь на охрану, находится в интервале от 396 до 404. Таким образом можно утверждать, что служащие автостоянки обманывают ее владельца.
Пример 7.4 В 24-х из 40 проверок число автомобилей на автостоянке не превышало 400 единиц. С вероятностью 0,98 найдите доверительный интервал для оценки истинной доли дней в течение года, когда число оставляемых на стоянку автомобилей не превышало 400 единиц. Решение. Определим границы доверительного интервала для доли дней в течение года, когда число оставляемых на стоянку автомобилей не превышало 400 единиц. По условию: m = 24; n = 40; g = 0,98. Выборочная доля Так как то найдем t из соотношения 2F0(t) = g: 2F0(t) = 0,98; F0(t) = 0,98 / 2 = 0,49. По таблице функции Лапласа (приложение 2) найдем при каком t F0(t) = 0,49. F0(2,33) = 0,49. Следовательно, t = 2,33. Найдем предельную ошибку выборки:
Ответ. С вероятностью 0,98 можно ожидать, что доля дней в течение года, когда число оставляемых на стоянку автомобилей не превышало 400 единиц, находится в интервале от 0,4297 до 0,7703. Пример 7.5 Изменим условие примера 7.3. С помощью собственно-случайного бесповторного отбора определяется среднее число автомобилей, оставляемых на ночь на охрану. Предполагается, что оно подчиняется нормальному закону. Каким должен быть объём выборки, чтобы с вероятностью 0,95 можно было утверждать, что принимая полученное среднее число автомобилей по выборке за истинное, совершается погрешность, не превышающая 3 автомобилей, если среднее квадратическое отклонение s равно 10 автомобилям? Решение. Дано: D = 3; s = 10; g = 0,95;N=365. Воспользуемся формулой расчета необходимой численности выборки для средней для собственно-случайного бесповторного отбора:
Найдем t из соотношения 2F0(t) = g: 2F0(t) = 0,95; F0(t) = 0,95 / 2 = 0,475; По таблице функции Лапласа (приложение 2) найдем при каком t F0(t) = 0,475. F0(1,96) = 0,475. Следовательно, t = 1,96. Рассчитаем объём выборки:
Так как n - целое число, а также, учитывая необходимость не превысить заданную ошибку, округлим полученный результат до большего целого. Следовательно, необходимо провести не менее 39 проверок. Ответ. Для определения среднего числа автомобилей, оставляемых на ночь на охрану с вероятностью 0,95 и D=3, необходимо, необходимо провести не менее 39 проверок.
Пример 7.6 Изменим условие примера 7.4. Каким должен быть объём собственно-случайной бесповторной выборки, чтобы с вероятностью 0,9 можно было утверждать, что максимальное отклонение выборочной доли дней от доли дней в течение года (когда среднее число оставляемых на охрану автомобилей не превышало 400 единиц) не превышало 0,1, если по данным прошлых проверок выборочная доля таких дней составляла 0,6? Решение. Дано: D = 0,1; w = 0,6; g = 0,9;N=365. Воспользуемся формулой расчета необходимой численности выборки для доли при собственно-случайном бесповторном отборе:
Найдем t из соотношения 2F0(t) = g: 2F0(t) = 0,9; F0(t) = 0,9 / 2 = 0,45. По таблице функции Лапласа (приложение 2) найдем при каком t F0(t) = 0,45. F0(1,64) = 0,45. Следовательно, t = 1,64. Рассчитаем необходимую численность выборки:
Так как n - целое число, а также, учитывая необходимость не превысить заданную ошибку, округлим полученный результат до большего целого. Следовательно, n» 55. Ответ. Для того чтобы с вероятностью 0,9 и предельной ошибкой 0,1 с помощью собственно-случайного бесповторного отбора определить искомую долю дней в течение года, необходимо провести не менее 55 проверок.
Пример 7.7 Служба контроля Энергосбыта провела выборочную проверку расхода электроэнергии жителями одного из многоквартирных домов. С помощью собственно-случайного отбора выбрано 10 квартир и определен расход электроэнергии в течение одного из летних месяцев (кВт-час): 125; 78; 102; 140; 90; 45; 50; 125; 115; 112. С надежностью 0,95 определите доверительный интервал для оценки среднего расхода электроэнергии на 1 квартиру во всем доме при условии, что в доме 70 квартир, а отбор был: а) повторным; б) бесповторным. Решение. По условию задачи выборочное обследование проведено с помощью собственно-случайного отбора. Объем выборки n = 10 единиц, т.е. выборка - малая. а) Считая отбор повторным, найдем доверительный интервал для оценки среднего расхода электроэнергии на 1 квартиру во всем доме, т.е. границы доверительного интервала для оценки генеральной средней. Для этого используем формулы:
Для определения границ доверительного интервала необходимо рассчитать выборочные среднюю и среднее квадратическое (стандартное) отклонение. Рассчитаем выборочную среднюю арифметическую:
Найдем исправленную выборочную дисперсию:
Найдем исправленное выборочное среднее квадратическое отклонение:
Итак, дано: По таблице Стьюдента (Приложение 5) найдем t по уровню значимости a и числу степеней свободы k. a = 1 - g = 1 - 0,95 = 0,05; k = n - 1 = 10 - 1 = 9. ta=0,05; k=9= 2,26. Найдем предельную ошибку выборки:
Ответ. При условии, что отбор квартир был повторным, с вероятностью 0,95 можно ожидать, что средний расход электроэнергии на 1 квартиру во всем доме находится в интервале от 75,2269 до 121,1731 кВт-часа.
б) Найдем границы доверительного интервала для оценки среднего расхода электроэнергии на 1 квартиру во всем доме, считая отбор бесповторным. Для этого используем формулы:
По условию: Найдем предельную ошибку выборки:
Ответ. При условии, что отбор квартир был бесповторным, с вероятностью 0,95 можно ожидать, что средний расход электроэнергии на 1 квартиру во всем доме находится в интервале от 76,9311 до 119,4689 кВт-часа. Задачи к теме 7
1. Результаты 10-ти дневного наблюдения в молочном отделе супермаркета показали, что в среднем в день реализуется 144 пачки творога с исправленным средним квадратическим отклонением в 23 пачки. Оцените потребность супермаркета в закупке творога, построив 99% доверительный интервал.
2. Фирма, торгующая автомобилями в небольшом городе, собирает информацию о состоянии местного автомобильного рынка в текущем году. С этой целью из 8500 горожан в возрасте 18 лет и старше, отобрано 500 человек. Среди них оказалось 130 человек, планирующих приобрести новый автомобиль в текущем году. Оцените долю лиц в генеральной совокупности в возрасте 18 лет и старше, планирующих приобрести новый автомобиль в текущем году, если a = 0,01. 3. При выборочном опросе 1200 телезрителей оказалось, что 456 из них регулярно смотрят программы телеканала НТВ. Постройте 99%-ный доверительный интервал, оценивающий долю всех телезрителей, предпочитающих программы телеканала НТВ. 4. Выборочные обследования показали, что доля покупателей, предпочитающих новую модификацию зубной пасты, составляет 60% от общего числа покупателей данного товара. Каким должен быть объём выборки, чтобы можно было получить оценку генеральной доли с точностью не менее 0,1 при доверительной вероятности 0,954? 5. Среднемесячные расходы на питание домохозяйств из трех человек оцениваются по случайной выборке. С вероятностью 0,997 определите объем выборки, необходимой для такой оценки, если ошибка выборки не должна превышать 500 рублей, а по результатам более ранних исследований среднее квадратическое отклонение составило 2000 рублей.
6. Менеджер компании, занимающейся прокатом автомобилей, хочет оценить среднюю величину пробега одного автомобиля в течение месяца. Из 280 автомобилей, принадлежащих компании, методом случайной бесповторной выборки отобрано 35. По данным этой выборки установлено, что средний пробег автомобиля в течение месяца составляет 1342 км со стандартным отклонением 227 км. Считая пробег автомобиля случайной величиной, распределённой по нормальному закону, найти 95%-ный доверительный интервал, оценивающий средний пробег автомобилей всего парка в течение месяца.
7. Выборочные маркетинговые исследования показали, что 68% потребителей предпочитают приобретать черный чай без вкусовых добавок. Определите границы 95%-ного доверительного интервала доли таких потребителей в генеральной совокупности, если объем выборки составил 500 человек.
8. Выборочное исследование деятельности коммерческих банков региона показало, что в среднем каждый банк имеет 14 филиалов в регионе (со стандартным отклонением, равным 8). Найти объем выборки, позволивший сделать такую оценку, если предельная ошибка оценки генеральной средней находится в пределах 20% от ее выборочного среднего значения, а доверительная вероятность составляет 0,95.
9. Выборочное обследование распределения населения города по среднедушевому денежному доходу показало, что 25% обследованных в выборке имеют доход ниже прожиточного минимума. В каких пределах с надежностью 0,954 находится доля населения, имеющего среднедушевой доход ниже прожиточного минимума, в генеральной совокупности, если в городе проживает 1 млн. чел. и выборочное обследование осуществляется с помощью собственно-случайного бесповторного отбора?
10. Аудиторская фирма хочет проконтролировать состояние счетов одного из коммерческих банков. Для этого случайно отбираются 55 счетов. По 21 счету из 55 отобранных имело место движение денежных средств в течение месяца. Построить 95%-ный доверительный интервал, оценивающий долю счетов в генеральной совокупности, по которым имело место движение денежных средств в течение месяца. 11. Выборочные обследования, проведенные администрацией строительных магазинов города, показали, что 45% горожан планируют ремонт квартиры или дома в течение следующих трех лет. Каким должен быть объем выборки, чтобы можно было получить оценку генеральной доли с точностью не менее 0,05 при доверительной вероятности 0,95, если в городе проживает 500000 человек? 12. Предварительный опрос покупателей магазина рыболовных принадлежностей «Серебряный ручей» показал, что 25% из них планируют в дальнейшем делать покупки в этом магазине, если им будет предоставлена дисконтная карта. Каким должен быть объем выборки, необходимый для оценки генеральной доли постоянных покупателей, при заданной точности не менее 0,04 и доверительной вероятности 0,954? 13. Среднемесячный бюджет студентов в колледжах одного из штатов США оценивается по случайной выборке. Найдите наименьший объём выборки, необходимый для такой оценки с вероятностью 0,954, если среднее квадратическое отклонение предполагается равным 100 у.е., а предельная ошибка средней не должна превышать 25 у.е.
14. Коммерческий банк, изучая возможности предоставления долгосрочных кредитов населению, опрашивает своих клиентов для определения среднего размера такого кредита. Из 9700 клиентов банка опрошено 1000 человек. Среднее значение необходимого кредита в выборке составило 7750 у.е. со стандартным отклонением 1560 у.е. Найдите границы 95%-ного доверительного интервала для оценки неизвестного среднего значения кредита в генеральной совокупности. 15. Выборочное обследование показало, что 20% студентов университета нуждаются в общежитии. Каким должен быть объем случайной бесповторной выборки, в результате которой будет оценена генеральная доля с точностью не менее 0,03 при доверительной вероятности 0,954, если в университете обучается 5000 студентов дневного отделения? 16. По предварительным данным коммунальных служб города 10% потребителей имеют задолженности по оплате коммунальных услуг. Каким должен быть объем выборки, необходимой для оценки генеральной доли задолжников, если предельная ошибка выборки не должна превышать 0,05 при доверительной вероятности 0,954? 17. Строительная компания хочет оценить возможности успешного бизнеса на рынке ремонтно-строительных работ. Каким должен быть объем выборки среди 1200 клиентов строительной фирмы, если среднее квадратическое отклонение по результатам пробного обследования составило 850 у.е., а предельная ошибка выборки не должна превышать 200 у.е.? 18. По данным автосалона, услугами гарантийного ремонта в течение года гарантии воспользовались 28% покупателей автомобилей. Постройте 95% доверительный интервал доли покупателей, пользующихся гарантийным ремонтом, если автосалон продал за год 297 автомобилей.
19. Опрос 20 горожан показал, что среднемесячные расходы на покупку журналов и газет составляют 125 рублей с исправленным средним квадратическим отклонением 60 рублей. Постройте 99% доверительный интервал для оценки среднемесячных расходов на прессу горожан в генеральной совокупности.
20. Для определения среднего размера дневной выручки маршрутных такси города была произведена 10%-ная случайная бесповторная выборка из 1200 маршрутных такси. В результате были получены данные о средней дневной выручке, которая составила 5000 рублей. В каких пределах с доверительной вероятностью 0,95 может находиться средняя дневная выручка всех маршрутных такси города, если среднее квадратическое отклонение составило 650 рублей?
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 684; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.192.89 (0.009 с.) |






 - выборочная дисперсия значений признака;
- выборочная дисперсия значений признака; - выборочная дисперсия доли значений признака;
- выборочная дисперсия доли значений признака;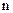 - объем выборки;
- объем выборки; - объем генеральной совокупности;
- объем генеральной совокупности; - доля обследованной совокупности;
- доля обследованной совокупности; - поправка на конечность совокупности[4].
- поправка на конечность совокупности[4]. и экономичность проводимого выборочного наблюдения, т.к. чем больше объем выборки, тем больше затраты на изучение элементов выборки, но тем меньше при этом ошибка выборки.
и экономичность проводимого выборочного наблюдения, т.к. чем больше объем выборки, тем больше затраты на изучение элементов выборки, но тем меньше при этом ошибка выборки. и формул средних ошибок выборки определяются формулы необходимой численности выборки для различных способов отбора.
и формул средних ошибок выборки определяются формулы необходимой численности выборки для различных способов отбора.



 . Если
. Если  представляет собой предел, которым ограничена сверху абсолютная величина
представляет собой предел, которым ограничена сверху абсолютная величина  , то
, то  . Следовательно,
. Следовательно, (7.4)
(7.4) . (7.5)
. (7.5) ) или 0,05 вероятность ошибки. Обычно в статистике уровень значимости выбирают таким, чтобы он не превысил 5% (
) или 0,05 вероятность ошибки. Обычно в статистике уровень значимости выбирают таким, чтобы он не превысил 5% ( при известном среднем квадратическом отклонении s генеральной совокупности (на практике - при большом объеме выборки, т.е. при n ³ 30) и собственно-случайном повторном отборе формула (7.5.2) примет вид:
при известном среднем квадратическом отклонении s генеральной совокупности (на практике - при большом объеме выборки, т.е. при n ³ 30) и собственно-случайном повторном отборе формула (7.5.2) примет вид: (7.6)
(7.6) - среднее квадратическое отклонение;
- среднее квадратическое отклонение;
 при известном среднем квадратическом отклонении s генеральной совокупности (при большом объеме выборки, т.е. при n
при известном среднем квадратическом отклонении s генеральной совокупности (при большом объеме выборки, т.е. при n  30) и собственно-случайном бесповторном отборе формула (7.6) примет вид:
30) и собственно-случайном бесповторном отборе формула (7.6) примет вид: (7.7)
(7.7)
 (7.8)
(7.8)
 (7.9)
(7.9)
 при большом объеме выборки, т.е. при n
при большом объеме выборки, т.е. при n  (7.10)
(7.10)
 (7.11)
(7.11)
 (7.12)
(7.12)
 (7.13)
(7.13)
 = 8,7; s = 2,7; n = 900; g = 0,95.
= 8,7; s = 2,7; n = 900; g = 0,95.
 ;
; .
. ;
; ;
;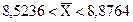 .
.
 .
. ;
; .
. ;
; ;
; .
. .
. .
. .
. .
. 0,05 с помощью собственно-случайного повторного отбора определить долю женщин во всем коллективе фирмы, необходимо обследовать не менее 226 служащих.
0,05 с помощью собственно-случайного повторного отбора определить долю женщин во всем коллективе фирмы, необходимо обследовать не менее 226 служащих. = 400; s = 10; n = 40; g = 0,99; N=365
= 400; s = 10; n = 40; g = 0,99; N=365 .
. ;
; .
. ;
; .
.
 ,
, ;
;
 ;
; .
. .
. .
. .
. .
. ;
; .
. .
.

 .
. .
. ;
; .
. .
. .
. .
. ;
; .
.


