Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полную группу можно определить так: еслиСодержание книги
Поиск на нашем сайте
Вероятностью появления события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных и несовместных элементарных исходов. Обозначим число благоприятствующих событию А исходов через М, а число всех исходов - N.
Относительной частотой события называется отношение числа испытаний m, при которых событие появилось, к общему числу проведенных испытаний n .
Статистической вероятностью события А называется относительная частота (частость) этого события, вычисленная по результатам большого числа испытаний. Будем обозначать её Р * (А). Следовательно, Для определения вероятности выпадения 1 или 2 при подбрасывании кости нам необходимо только знать “модель игры “, в данном случае - кость с 6 гранями. Мы можем определить наши шансы теоретически, без подбрасывания кости, это - априорная (доопытная) вероятность. Во втором примере мы можем определить вероятность только по результатам опыта, это - апостериорная (послеопытная) вероятность. То есть классическая вероятность - априорная, а статистическая - апостериорная. Какой бы вид вероятности не был выбран для их вычисления и анализа используется один и тот же набор математических правил.
Свойства вероятности, вытекающие из классического определения. 1. Вероятность достоверного события равна 1, то есть Р( Действительно, если событие А = 2.Если событие невозможное, то его вероятность равна 0, то есть Р(Æ)= 0. Если А = Æ, то оно не осуществится ни при одном испытании, то есть M = 0 и Р(Æ) = 0/N = 0. 3.Вероятность случайного события есть положительное число, заключенное между 0 и 1. В самом деле, та к как 0 4. Сумма вероятностей противоположных событий равна 1, то есть А отсюда:
Например, если вероятность извлечения туза из колоды, состоящей из 52 карт, равна 4/52, то вероятность извлечения карты, не являющейся тузом, равна 1 - 4/52 = 48/52. Пример 2.1 Магазин в целях рекламы нового товара проводит лотерею, в которой 1 главный приз, 5 вторых призов, 100 третьих призов и 1000 четвертых призов. В конце рекламного дня выяснилось, что лотерейные билеты получили 10000 покупателей. По правилам розыгрыша, после извлечения выигрышного билета он не возвращается в урну, и покупатель не может получить более одного выигрыша. Чему равна вероятность того, что покупатель, который приобрел рекламируемый товар: а) выиграет первый приз; б) выиграет хотя бы один приз; в) не выиграет ни одного приза? Решение. Определим событие А: «Покупатель выиграл первый приз». Согласно условию задачи в лотерее участвовало 10000 покупателей, отсюда общее число испытаний N = 10000, а число исходов, благоприятствующих событию А, M = 1. Все исходы являются равновозможными, единственно возможными и несовместными элементарными событиями. Следовательно, по формуле классической вероятности: P (A)=0,0001 Соответственно, определим событие В: «Покупатель выиграл любой приз». Для этого события число благоприятствующих исходов M = 1 + 5 + 100 + 1000 = 1106.
Событие «Покупатель не выиграет ни одного приза» - противоположное событию В: «Покупатель выиграет хотя бы один приз», поэтому обозначим его как
Ответ. Вероятность того, что покупатель выиграет первый приз, равна 0,0001; любой приз - 0,1106; ни одного приза - 0,8894. . Пример 2.2. Структура занятых в региональном отделении крупного банка имеет следующий вид:
Если один из служащих выбран случайным образом, то какова вероятность, что он: 1. Мужчина-администратор? 2. Женщина-операционист? 3. Мужчина? 4. Операционист? Решение. 1. В банке работают 100 человек, N = 100. Из них 15 – мужчины-администраторы, M = 15. Следовательно,
35 служащих в банке – женщины-операционисты, следовательно,
3. 40 служащих в банке – мужчины, следовательно,
4. Из общего числа служащих в банке 60 – операционисты, следовательно,
Ответ. Вероятность того, что один из служащих: 1. 2. 4.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 523; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.249.191 (0.006 с.) |

 для любой пары (i ¹ j), тогда {A1, A2, …, An} - полная группа событий.
для любой пары (i ¹ j), тогда {A1, A2, …, An} - полная группа событий. 
 M
M 
 . При очень большом числе испытаний статистическая вероятность приближенно равна классической вероятности, т.е. Р * (A)» Р(A)
. При очень большом числе испытаний статистическая вероятность приближенно равна классической вероятности, т.е. Р * (A)» Р(A) ) = 1.
) = 1. . В самом деле,
. В самом деле, 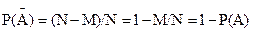
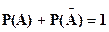
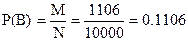 .
. . По формуле 2.3 найдем:
. По формуле 2.3 найдем: .
.
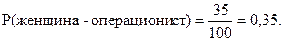
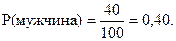


 3.
3.