
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сущность выборочного наблюденияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сущность выборочного наблюдения – определить пределы генеральной средней величины ( · для количественного признака сущность раскрывается в следующей формуле:
которая определяет пределы генеральной средней величины · для качественного признака пределы генеральной доли (удельного веса) определяются по формуле: P = w
6.5. Расчет необходимого объема выборки
Так как величина ошибки выборки зависит от численности выборочной совокупности n, при подготовке выборочного наблюдения возникает задача определения необходимой численности собственно-случайной выборки – такой, которая обеспечит заданную точность результатов исследования.
6.5.1. При повторном отборе необходимая численность выборки определяется по формулам:
6.5.2. При бесповторном отборе необходимая численность выборки определяется по формулам:
Полученный на основе использования этих формул результат всегда округляется в большую сторону до целого значения.
Малая выборка В практике статистических исследований массовых процессов и явлений часто приходится сталкиваться с небольшими по объему выборками, которые так и называются – «малые выборки». Малая выборка – это такое выборочное наблюдение, численность единиц которого не превышает 30. Малая выборка в настоящее время используется более широко, чем раньше, за счет того, что на ее организацию требуется гораздо меньше временных, материальных и трудовых затрат, чем на сплошное статистическое обследование. Кроме того, в настоящее время появляется все большее количество новых форм массовых явлений и процессов (в основном связанных с развитием рыночных отношений в экономике), число которых позволяет говорить об их немногочисленности, иногда единичности. Поэтому, иногда приходится ограничиваться малым числом наблюдений. При оценке результатов малой выборки для определения возможных пределов ошибки используется критерий Стьюдента, определяемый по формуле:
t – коэффициент доверия, затабулированный в специальных таблицах Стьюдента. Расчет ошибок в малой выборке мало отличается от аналогичных вычислений в большой выборке. Правда, в малой выборке вероятность будет немного меньше, чем в большой; и точность результатов выборки малого объема все же ниже, чем при большой выборке.
Решение типовых задач 6.7.1. Из партии электроламп взята 20%-ная случайная бесповторная выборка для определения среднего веса спирали. Результаты выборки следующие:
Определитес вероятностью λ = 0,95 (при этом определяем по таблице, что коэффициент доверия t = 1,96 ) доверительные пределы, в которых лежит средний вес спирали, для всей партии электроламп.
Решение: Доверительные интервалы для генеральной средней с вероятностью λ:
Δx = По условию задачи
Определяем доверительные интервалы для генеральной средней с вероятностью λ = 0,95:
6.7.2. В микрорайоне проживает 5000 семей. В порядке случайной бесповторной выборки предполагается определить средний размер семьи при условии, что ошибка выборочной средней не должна превышать 0,8 человека с вероятностью λ = 0,954 и при среднем квадратическом отклонении 3,0 человека.
Решение. Так как при λ = 0,954 t=2, то в этом случае необходимая численность выборки равна:
6.7.3. На заводе электроламп из партии продукции в количестве 16 000 шт. ламп взято на выборку 1600 шт. (случайный, бесповторный отбор), из которых 40 шт. оказались бракованными. Определитес вероятностью 0,997 пределы, в которых будет находиться процент брака для всей партии продукции.
Решение: 1.Определяем долю бракованной продукции в выборке:
2.При вероятности 3.Размер предельной ошибки:
или 1,1%. 4.Доверительные интервалы для генеральной доли с вероятностью
следовательно: или Можно сказать с вероятностью l = 0,997, что во всей партии продукции процент брака будет находиться в пределах от 1,4% до 3,6%.
6.7.4. На основе выборочного обследования в отделении связи города предполагается определить долю писем частных лиц в общем объеме отправляемой корреспонденции. Никаких предварительных данных об удельном весе этих писем в общей массе отправляемой корреспонденции не имеется. Определитечисленность выборки, и результаты выборки дайте с точностью до 1% и гарантией этого с вероятностью λ =0,95, при доле выборки = 0,5 ( Решение: По условию задачи известны: Размер допустимой (предельной) ошибки - принятая вероятность – λ = 0,95; при λ = 0,95 t (коэффициент доверия) = 1,96. Необходимая численность выборки: n =
Таким образом, чтобы с заданной точностью определить долю частных писем в общем объеме отправляемой корреспонденции, необходимо в порядке случайной выборки отобрать 9604 письма.
6.7.5. По городской телефонной сети в порядке случайной выборки (механический отбор) произвели 100 наблюдений и установили среднюю продолжительность одного телефонного разговора - 5 минут при среднеквадратическом отклонении 2 минуты. Какова вероятность того, что ошибка репрезентативности при определении средней продолжительности телефонного разговора не превысит 18 секунд?
Решение: По условию задачи известно: Объем выборки – n =100; Выборочная средняя Выборочное среднеквадратическое отклонение σ = 2 мин.; Предельная ошибка выборки - Следовательно, согласно имеющимся формулам:
Затем по таблице значений «t» на основе полученного в результате вычислений t определяем вероятность того, что ошибка не превысит заданной величины: при t = 1,5 вероятность λ = 0,866.
Следовательно, с вероятностью λ = 0,866 можно утверждать, что ошибка репрезентативности при определении средней продолжительности телефонного разговора не превысит 18 секунд.
6.7.6. Необходимо провести социологическое исследование с вероятностью 95,4% (λ = 0,954), посвященное опознанию потребителями торговой марки. Предельно допустимая ошибка данного исследования не должна превышать 5%. Какое количество респондентов необходимо опросить в порядке собственно случайной повторной выборки для решения данной проблемы?
Решение:
Следовательно, обследованию необходимо подвергнуть не менее 400 респондентов не предмет узнаваемости торговой марки компании.
6.8. Задания для самостоятельной работы Задача 1. В ОАО «Протекс» работает 3640 человек. Методом случайной бесповторной выборки обследовано 1120 человек, из которых 800 выполняли и перевыполняли дневную норму выработки. Определите: 1) долю рабочих, не выполняющих норму выработки, по данным выборочного обследования; 2) долю всех рабочих акционерного общества, не выполняющих норму (с вероятностью λ=0,954). Задача 2. На предприятии в порядке случайной бесповторной выборки было опрошено 100 рабочих из 1000 и получены следующие данные об их доходе за октябрь:
Определите: 1) среднемесячный размер дохода у работников данного предприятия, гарантируя результат с вероятностью λ=0,997; 2) долю рабочих предприятия, имеющих месячный доход 6800 руб. и выше, гарантируя результат с вероятностью λ=0,954; 3) необходимую численность выборки при определении среднего месячного дохода работников предприятия, чтобы с вероятностью λ=0,954 предельная ошибка выборки не превышала 100 руб.; 4) необходимую численность выборки при определении доли рабочих с размером месячного дохода 6800 руб. и выше, чтобы с вероятностью λ=0,954 предельная ошибка не превышала 4%.
Задача 3. Для выявления текущих потерь рабочего времени на производственном участке цеха был использован метод моментных наблюдений. За смену было произведено 84 наблюдения и получено 6 отметок о простое рабочих. Определитес вероятностью λ=0,954 доверительные интервалы текущих потерь рабочего времени на производственном участке цеха. Задача 4. Для исследования естественной порчи имеющихся на складе товаров сделано их 5-%-ное выборочное обследование. В результате лабораторного анализа установлено следующее распределение полученных посредством механической выборки образцов:
На основе показателей выборочной совокупности для всей партии товара, т.е. генеральной совокупности, определите: 1) с вероятностью λ=0,954 возможные пределы доли продукции с естественной убылью от 10% и выше, т.е. размер нестандартной (испорченной) продукции; 2) с вероятностью λ= 0,997 возможные пределы среднего процента естественной порчи товаров.
Задача 5. Из партии изготовленных изделий общим объемом 4000 единиц проверено посредством механической выборки 40% изделий, из которых бракованными оказались 13 изделий. Определите: 1) долю бракованных изделий по данным выборки; 2) пределы, в которых находится процент бракованных изделий, для всей партии (с вероятностью λ=0,954).
Задача 6. В результате выборочного обследования покупателей супермаркета (случайная повторная выборка) получено следующее распределение по размеру сделанных покупок:
С вероятностью λ=0,997 определите: а) границы среднего размера покупки; б) границы удельного веса покупок на сумму до 100 руб.
Задача 7. Из партии готовой продукции с целью проверки ее соответствия технологическим требованиям произведена 10%-ная случайная бесповторная выборка, которая привела к следующим результатам:
Можно ли принять всю партию при условии, что доля изделий с весом 51 грамм и более с вероятностью λ=0,997 не должна превышать 6%?
Задача 8. Как изменится необходимый объем собственно-случайной повторной выборки, если уровень вероятности, с которым требуется получить результат, увеличить с λ= 0,954 до λ=0,997? Задача 9. Для выборочного контроля знаний студентов в порядке случайной бесповторной выборки было отобрано и протестировано 185 человек, что составило 4% от общего контингента студентов ВУЗа. В результате тестирования 5 студентов показали неудовлетворительные результаты. Можно ли с вероятностью λ=0,954 утверждать, что доля студентов с неудовлетворительными знаниями в целом по ВУЗу не превышает 6%?
Задача 10. Сколько покупателей супермаркета необходимо охватить в процессе выборочного наблюдения, чтобы с вероятностью λ=0,997 определить границы среднего размера покупки с предельной ошибкой 200 руб.? Для получения данных о вариации размера покупок воспользуйтесь следующими данными:
Задача 11. На основе 4%-ного выборочного обследования (случайная бесповторная выборка) получены следующие данные о расходах населения на оплату жилищно-коммунальных услуг:
С какой вероятностью λ можно утверждать, что удельный вес домохозяйств, расходующих на оплату жилищно-коммунальных услуг более 2100 руб. в месяц, в целом по данному региону не превышает 9,4%?
Задача 12. Определите, сколько телефонных звонков необходимо обследовать оператору мобильной связи в порядке случайной выборки, чтобы с вероятностью λ=0,954 установить долю разговоров продолжительностью свыше 10 минут. Допустимая величина предельной ошибки 3%.
Задача 13. В результате выборочного обследования населения области установлено, что с вероятностью λ=0,954 среднедушевые доходы находятся в интервале от 6830 до 8260 руб. в месяц. Определите границы среднедушевых доходов с вероятностью λ=0,997? Задача 14. Планируется обследование населения с целью определения средних расходов на медицинские услуги и лекарственные средства. Определите необходимый объем собственно-случайной бесповторной выборки, чтобы получить результаты с точностью +/- 100 руб. при уровне вероятности λ=0,954. Известно, что в районе проживает 77 тыс. человек, а пробное обследование показало, что среднее квадратическое отклонение расходов населения на эти цели составляет 180 руб.
Задача 15. 2%-ное выборочное обследование торговых предприятий района с целью изучения цен на молоко привело к следующим результатам:
С вероятностью λ=0,997 определите границы средней цены 1 литра молока в целом по данному району.
Задача 16. Пробное выборочное обследование каждого сорокового малого предприятия области привело к следующим результатам:
Определите, каким должен быть интервал отбора при механической выборке, чтобы получить данные о средней численности занятых на малых предприятиях с точностью +/- 1 чел. при уровне вероятности λ=0,997? Задача 17. В результате выборочного контроля качества продукции установлено, что при уровне вероятности λ=0,997 доля некондиционных изделий не превышает 6,2%. При этом доля некондиции в выборке составила 0,06. Можно ли с вероятностью λ=0,954 утверждать, что некондиционная продукция в тестируемой партии не превышает 8,5%?
Задача 18. Определите, сколько клиентов автосервиса, отобранных случайной выборкой, необходимо опросить для определения доли лиц, неудовлетворенных качеством обслуживания. При этом предельная ошибка не должна превышать 2,5% при уровне вероятности λ=0,954. Из аналогичных обследований известно, что дисперсия данного альтернативного признака (неудовлетворенность качеством обслуживания) не превышает 0,24.
Задача 19. В результате опроса каждого шестого учащегося выпускных классов школ района было выяснено, что среднее время, затрачиваемое ежедневно на подготовку к занятиям, составляет 88 минут при коэффициенте вариации 28,6%. При этом выборочная совокупность составила 134 человека. С вероятностью λ=0,954 определите границы средних затрат времени на подготовку к занятиям в целом по всем учащимся выпускных классов школ района?
Задача 20. Определите, сколько выпускных классов необходимо охватить обследованием, чтобы вычислить средние расходы школьников на подготовку к поступлению в ВУЗы с предельной ошибкой 1500 руб. и уровнем вероятности λ=0,954, если известно, что в районе 249 выпускных классов, а дисперсия расходов, по данным прошлогоднего обследования, составила 99 тыс.рубей.
??? ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 1. Цели проведения выборочного обследования? 2. В чем заключаются особенности и каково значение выборочного наблюдения? 3. Сущность выборочного наблюдения? 4. Что такое генеральная и выборочная совокупности? 5. Приемы формирования выборочной совокупности? 6. Оценка выборочной совокупности? 7. Что такое ошибка выборочного наблюдения, по какой формуле она исчисляется и от каких факторов зависит её величина? 8. Понятие альтернативного прищзнака? 9. Повторная и бесповторная выборки. Какая из них точнее? 10. Отличие предельной ошибки выборки от средней ошибки? 11. Определение необходимой численности выборки при заданной её точности? 12. Способы распространения данных выборочных обследований?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 4089; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.78.249 (0.01 с.) |

 ) или генеральной доли (Р).
) или генеральной доли (Р). ,
, .
.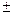 Dw
Dw 



 - при оценивании среднего значения выборки;
- при оценивании среднего значения выборки; - при оценивании выборочной доли.
- при оценивании выборочной доли. , где
, где -мера случайных колебаний выборочной средней в малой выборке,
-мера случайных колебаний выборочной средней в малой выборке, , где:
, где: - средний уровень признака по выборке.
- средний уровень признака по выборке. мг
мг t = t
t = t 
 или 0,2, следовательно N =
или 0,2, следовательно N =  шт.
шт.
 мг.
мг. или
или 
 семей
семей или 2,5%
или 2,5% t = 3,0 (находим по таблице)
t = 3,0 (находим по таблице)



 = 0,5).
= 0,5). = 1%, или 0,01;
= 1%, или 0,01;
 = 9604.
= 9604. ,
,
 t =
t = 




