
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет показателей вариации стажа работы продавцовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вычисляем средний стаж работы:
Вычисляем дисперсию:
Следует иметь в виду, что дисперсия – безмерная величина и самостоятельного экономического значения не имеет. Дисперсия необходима для расчета среднего квадратического отклонения. В данном случае среднее квадратическое отклонение равно:
Среднее квадратическое отклонение показывает, что в среднем варианты отклоняются от средней арифметической ( Для характеристики степени колеблемости признака необходимо среднее квадратическое отклонение выразить в процентах к средней арифметической, т.е. вычислить коэффициент вариации (V):
Коэффициент вариации свидетельствует о том, что колеблемость стажа работы продавцов весьма значительна и неоднородна. 5.7.4. Определите первый и третий квартили интервального ряда по данным о содержании бракованных товаров в поступившей в магазин партии товара:
Решение: Первый и третий квартили имеющегося ряда определяем по формулам:
Следовательно, в ряду распределения по данным о бракованных товарах в поступившей партии товара в магазин первый квартиль составляет 14,3%, а третий – 18,0%, т.е. 25% товаров содержат брак, не превышающий 14,3%, а у 75% товаров процент брака не превышает 18%.
5.7.5. Определите 1-й и 9-й децили интервального ряда по данным о содержании влаги в поступившей в магазин партии товара:
Решение: Первый и девятый децили данных таблицы определяем по формулам:
Таким образом, значения децилей указывают на то, что среди 10% партии товара с минимальным процентом влажности максимальный процент ее составляет 13%, а среди 10% партии товара с наибольшим процентом влажности минимальный процент ее составил 20%, т.е. в 1,54 раза больше.
5.7.6. Имеются данные о времени работы (лет) 24 рабочих в цехе завода: Стаж рабочих в данном цехе (лет): 4; 3; 6; 4; 4; 2; 3; 5; 4; 4; 5; 2; 3; 4; 4; 5; 2; 3; 6; 5; 4; 2; 4; 3. Требуется: 1. построить дискретный ряд распределения, 2. дать графическое изображение ряда, 3. вычислить показатели центра распределения, показатели вариации и формы распределения. Решение: 1. Дискретный ряд распределения стажа рабочих в цехе завода:
2. Представим графическое изображение построенного дискретного вариационного ряда распределения рабочих по времени работы в цехе в виде полигона частот:
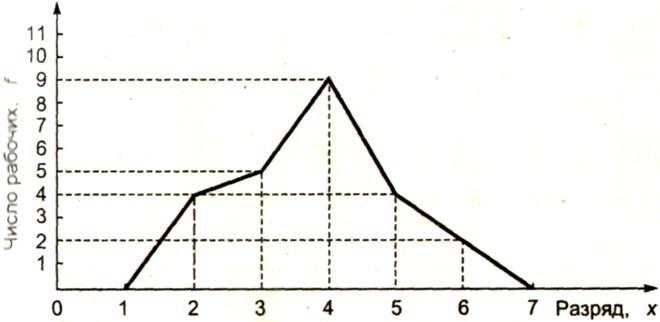
Полигон частот замыкается, для этого крайние вершины соединяются с точками на оси абсцисс, отстоящими на одно деление в принятом масштабе (в данном случае х = 1 и х = 7). 3. К показателям центра распределения относятся: средняя арифметическая, мода и медиана.
Средняя арифметическая (
Мода (М0) = 4 годам (4 года встречается 9 раз, т.е. это наибольшая частота f). Для определения медианы необходимо определить номер интервала, в котором она находится: NМе = Медиана (Ме) = 4 годам (так как номера 12 и 13 соответствуют 4 годам). К показателям вариации относятся: размах вариации (R), среднее линейное отклонение ( - размах вариации определяем по формуле:
R = Xmax – Xmin = 6 – 2 = 4 года
- для определения среднего линейного отклонения и других показателей вариации построим дополнительную таблицу вычислений:
Следовательно, индивидуальные значения отличаются в среднем от средней арифметической на 1,15 года, или на 30,3%. Среднее квадратическое отклонение превышает среднее линейное отклонение ( Значение коэффициента вариации (V = 30,3%) свидетельствует о том, что совокупность достаточно однородна. Как видно из построенного ранее полигона вариационного ряда распределение рабочих цеха по времени их работы в цехе несимметрично, поэтому определяется показатель асимметрии:
Следовательно, асимметрия левосторонняя, незначительная. 5.7.7. Распределение работников производственного предприятия по размеру месячной заработной платы следующее:
Определите коэффициент децильной дифференциации. Сформулируйте вывод.
Решение: Коэффициент децильной дифференциации определяется по формуле:
Для этого определяем место децилей:
Для расчета численных значений децилей определяем интервалы, в которых они находятся, для чего исчисляем накопленные частоты и результаты записываем в таблицу:
Из таблицы видно, что первая дециль находится в интервале 15,0 - 16,0, девятая дециль находится в интервале 18,0 – 19,0. Вычислим числовые значения децилей:
Следовательно, наименьший размер месячной заработной платы 10% наиболее обеспеченных работников в 1,21 раза выше наивысшего размера месячной заработной платы 10% наименее обеспеченных работников.
5.7.8. Имеются следующие данные о возрастном составе работников предприятий потребительской кооперации N - района (лет): 18, 38, 28, 29, 26, 38, 34, 22, 28, 30, 22, 23, 35, 33, 27, 24, 30, 32, 28, 25, 29, 26, 31, 24, 29, 27, 32, 25, 29, 29. Для анализа распределения работников предприятий потребительской кооперации по возрасту требуется: 1. построить интервальный ряд распределения; 2. исчислить показатели центра распределения, показатели вариации и формы распределения; 3. сформулировать выводы. Решение: 1. Величина интервала группировки определяется по формуле:
n (количество интервалов)– мы принимаем равным 7.
Полученный интервальный ряд распределения представим в таблице:
2. Рассчитываем показатели центра распределения (
где: Для определения численного значения моды (Мо) по нашему интервальному ряду определим, что она находится в интервале 27-30 лет, так как наибольшее число работников (f = 10) находится в этом интервале. Значение моды определяется по формуле:
= Для определения численного значения медианы (Ме) также сначала определяем интервал, в котором она находится:
Медианным является также интервал 27-30 лет, так как в этом интервале находятся номера 15 и 16 ряда.
Для расчета показателей вариации составим вспомогательную таблицу:
Следовательно, вариация возраста у работников предприятий потребительской кооперации не является значительной, что подтверждает достаточную однородность совокупности. Показатель асимметрии распределения работников по возрасту определяем по формуле:
Следовательно, асимметрия правосторонняя, незначительная. При правосторонней асимметрии между показателями центра распределения существует соотношение: Мо < Ме < Для данного распределения это соотношение выполняется, т.е. 28,3 < 28,6 < 28,7. Для имеющегося распределения, учитывая незначительную асимметрию, определяем показатель эксцесса (островершинности):
М4 – центральный момент четвертого порядка, σ4 - среднее квадратическое отклонение в четвертой степени.
Отрицательное значение эксцесса свидетельствует о плосковершинности данного распределения.
5.8. Задания для самостоятельной работы Задача 1. На основе группировки магазинов по размерам оборота розничной торговли за квартал определите: · средний размер оборота 1-го магазина; · среднее квадратическое отклонение; · коэффициент вариации.
Решение оформите в таблице.
Задача 2. Распределение подростковой преступности по одной из областей Российской Федерации за 1-ое полугодие 2010 г.:
Определите показатели вариации: а) размах; б) среднее линейное отклонение; в) среднее квадратическое отклонение; г) относительный размах вариации; д) относительное линейное отклонение. Оцените количественную однородность совокупности.
Задача 3. Распределение числа слов в телеграмме в двух почтовых отделениях характеризуется следующими данными:
Определите для каждого почтового отделения:
а) среднее число слов в одной телеграмме; б) среднее линейное отклонение; в) линейный коэффициент вариации; г) сравните вариацию числа слов в телеграмме.
Задача 4. Распределение длины пробега автофургона торговой фирмы характеризуется следующими данными:
Определите: а) среднюю длину пробега за 1 рейс; б) среднее квадратическое отклонение; в) коэффициент вариации. Оцените количественную однородность совокупности. Задача 5. Распределение численности безработных по возрастным группам в N-м регионе за 2008-2010 г. характеризуется следующими данными:
Определите: а) для каждого года средний возраст безработного; б) среднее квадратическое отклонение; в) коэффициент вариации. Сравните вариацию возраста безработных за два года.
Задача 6. Распределение коммерческих банков по размеру активов характеризуется следующими данными:
Определите общую дисперсию двумя способами: а) обычным; б) по способу моментов.
Задача 7. Товарооборот по предприятию общественного питания одного работника за квартал характеризуется следующими данными:
Определитепо каждому предприятию: коэффициент вариации и сравните вариацию товарооборота общественного питания в названных предприятиях. Сделайте выводы.
Задача 8. Средняя величина признака в совокупности равна 20, а средний квадрат индивидуальных значений этого признака – 400. Определитекоэффициент вариации.
Задача 9. Удельный вес основных рабочих в трех цехах предприятия составил: 80, 75 и 90% общей численности рабочих. Определитедисперсию и среднее квадратическое отклонение доли основных рабочих по предприятию в целом, если численность всех рабочих трех цехов составила соответственно 100, 200 и 150 человек. Задача 10. Дисперсия признака равна 360000, коэффициент вариации равен 50%. Чему равна средняя величина признака?
Задача 11. При проверке партии электроламп из 1000 штук 30 штук оказались бракованными. Определитедисперсию и среднее квадратическое отклонение.
Задача 12. Распределение рабочих предприятия по размеру месячного дохода следующее:
Определитекоэффициент квартильной дифференциации.
Сформулируйте вывод. Задача 13. Имеются следующие данные о распределении продовольственных магазинов региона по размеру товарооборота за месяц:
Требуетсявычислить средний месячный размер товарооборота магазинов региона, дисперсию и коэффициент вариации.
Задача 14. Средняя величина признака в совокупности равна 13, а средний квадрат индивидуальных значений этого признака равен 174. Определитекоэффициент вариации.
Задача 15. Выходной контроль качества поступающих комплектующих изделий дал следующие результаты:
Вычислите дисперсию доли брака по каждой поступившей партии.
Задача 16. Распределение рабочих двух участков по стажу работы следующее:
Определите, на каком участке состав рабочих по стажу работы более однороден.
Задача 17. По данным Госкомстата РФ численность занятых в экономике по возрасту в 2010 г. распределилась следующим образом:
Определитемедиану, первый и третий квартили, первый и девятый децили. Объясните их содержание.
Задача 18. Распределение безработных по длительности перерыва в работе N – го региона, характеризуется следующими данными:
Определитемедианные и квартильные значения продолжительности перерыва в работе, объясните их содержание и сделайте сравнительный анализ. Задача 19. Распределение коммерческих банков по величине кредитных вложений характеризуется следующими данными:
Определитеквартили и децили уровня кредитных вложений, объясните их содержание.
Задача 20. Распределение населения по величине среднедушевого денежного дохода в России за 2010 г. характеризуется следующими данными:
Для оценки степени децильной дифференциации населения определите децили среднедушевого дохода. Объясните их содержание.
Задача 21. Распределение фермерских хозяйств по посевной площади характеризуется следующими данными:
Определите дисперсию и среднее квадратическое отклонение посевных площадей, применив для расчета средней арифметической и дисперсии способ моментов.
Задача 22. Распределение строительных фирм по объему инвестиций характеризуется следующими данными:
Определите характеристики распределения: а) среднюю величину б) моду в) среднее квадратическое отклонение г) коэффициент вариации и асимметрии д) коэффициенты квартильного и децильного отклонения. Сделайте выводы об однородности и характере распределения строительных фирм. Задача 23. При исследовании трудовой активности сотрудников организации (отработано человеко-дней за год) получены средние величины и значения центральных моментов:
Используя показатели асимметрии и эксцесса, сравните характер распределения мужчин и женщин по трудовой активности. Сделайте выводы. ____________________________________________________________________
??? ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 1. Понятие общей и систематической вариации? 2. Виды показателей вариации и для каких целей они применяются? 3. Абсолютные показатели вариации и их исчисление? 4. Что такое среднее квадратическое отклонение и порядок его исчисления? 5. Среднее квартильное отклонение и порядок его исчисления? 6. Виды относительных показателей вариации? 7. Что такое коэффициент вариации, для каких целей он применяется и как рассчитывается? 8. Моменты в рядах распределения? 9. Начальный момент распределения и его порядок? 10. Центральный момент распределения и определение его порядка? 11. Ранговые показатели вариации: квартили, децили, процентили? 12. Средняя, мода и медиана в оценке асимметрии распределения? 13. Определение коэффициента асимметрии? 14. Показатель эксцесса распределения и определение его ошибок? 15. Понятие нормального, правостороннего и левостороннего распределения?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 4819; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.117.95 (0.014 с.) |

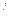 )
)
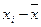 )
)

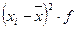
 =
= 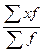 =
= 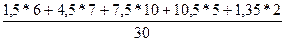 =
= 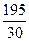 = 6,5 лет
= 6,5 лет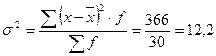
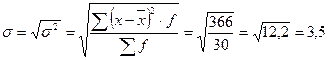 года.
года.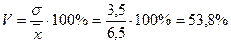 .
.
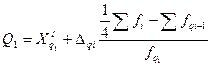 = 14+2
= 14+2 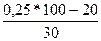 = 14,3%;
= 14,3%;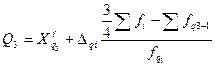 = 18+2
= 18+2 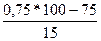 =18,0%.
=18,0%.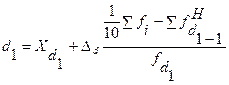 = 12+2
= 12+2 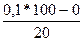 = 13%;
= 13%;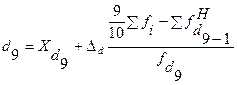 = 20+2
= 20+2 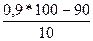 =20%.
=20%.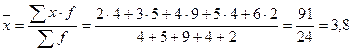 лет.
лет.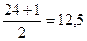 ;
;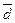 ), дисперсия (σ2), среднее квадратическое отклонение (σ), коэффициент вариации (V).
), дисперсия (σ2), среднее квадратическое отклонение (σ), коэффициент вариации (V).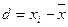
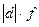
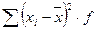
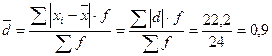 лет
лет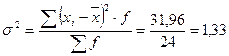
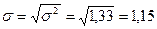 лет
лет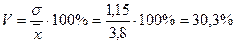
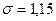 >
> 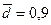 ) в соответствии со свойствами мажорантности средних величин.
) в соответствии со свойствами мажорантности средних величин.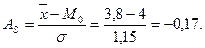

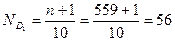 ;
; 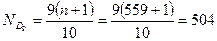
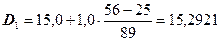 тыс.руб. или 15292,1 руб.
тыс.руб. или 15292,1 руб.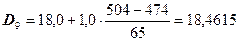 тыс.руб. или 18461,5 руб.
тыс.руб. или 18461,5 руб.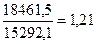
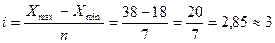 года
года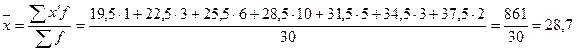 года,
года,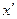 - среднее значение признака в интервале (центр каждого интервала).
- среднее значение признака в интервале (центр каждого интервала).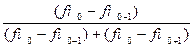 =
=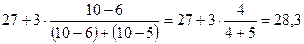 года.
года.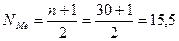
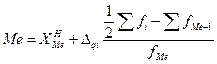 =
= 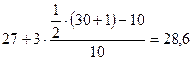 года.
года.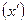
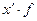
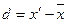
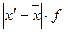
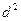
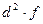
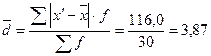 года
года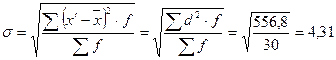 года
года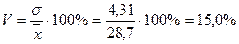 .
. .
.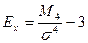 , где:
, где: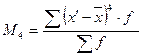 = =
= = 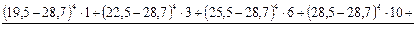
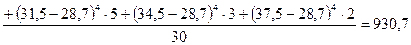
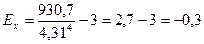 .
. М2
центральныемоменты М3
М4
М2
центральныемоменты М3
М4



