
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема №4. «вариационный анализ»Содержание книги
Поиск на нашем сайте Практическое занятие №1. Контрольные вопросы 1. Определите понятие «вариация». 2. Перечислите возможные причины вариации. 3. Что понимается под систематической и случайной вариацией? 4. Какие существуют показатели вариации? 5. Размах вариации. 6. Порядок расчета среднего линейного отклонения. 7. Понятие дисперсии признака. 8. Свойства дисперсии и ее расчет. 9. Что такое среднеквадратическое отклонение и каков порядок его вычисления? 10. Что такое коэффициент вариации, для каких целей он применяется и как рассчитывается?
Решение типовых задач Пример 4.1. Имеются следующие данные о распределении посевной площади фермерского хозяйства по урожайности пшеницы:
Требуется рассчитать все возможные показатели вариации. Решение: Рассчитаем следующие показатели вариации: размах вариации, среднее линейное отклонение; дисперсия; среднеквадратическое отклонение; коэффициент осцилляции; относительное линейное отклонение, коэффициент вариации. 1) размах вариации 2) среднее линейное отклонение вычисляется по формуле: здесь Дополним таблицу-условие столбцами: серединное значение интервала произведение модуль разности произведение модуля разности на частоту (повторяемость, или вес)
Заполним столбцы и найдём нужные суммы. Вычислим: среднюю урожайность среднее линейное отклонение 3) для вычисления дисперсии воспользуемся формулой где Вычислим: среднее квадрата значение дисперсии: 4) среднеквадратическое отклонение есть корень квадратный из дисперсии:
5) Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней и вычисляется по формуле:
6) Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины.
7) Коэффициент вариации является показателем однородности изучаемой совокупности:
Задачи для самостоятельного решения 4.1. Имеются следующие данные о распределении рабочих по тарифным разрядам:
Определите: 1) дисперсию; 2) среднеквадратическое отклонение; 3) коэффициент вариации.
4.2. С целью изучения производительности труда продавцов магазинов проведено исследование, результаты которого отображены в таблице:
Определить коэффициент вариации и осцилляции
4.3. На основании интервального ряда распределения магазинов по размеру товарооборота вычислите по всем магазинам торговой ассоциации: 1) средний размер товарооборота; 2) дисперсию и среднеквадратическое отклонение; 3) коэффициент вариации; 4) моду и медиану.
Решение задачи оформите в таблице.
4.4. На основании интервального ряда распределения числа работников предприятия по стажу, вычислите: 1) средний стаж работников предприятия; 2) дисперсию и среднеквадратическое отклонение; 3) коэффициент вариации; 4) моду и медиану.
Решение задачи оформите в таблице.
4.5. На основании интервального ряда распределения числа жителей по общей (полезно) площади их жилищ, приходящейся на одного человека, вычислите: 1) среднюю площадь жилища; 2) дисперсию и среднеквадратическое отклонение; 3) коэффициент вариации;
Решение задачи оформите в таблице.
4.6. На основании интервального ряда распределения магазинов по средней стоимости основных фондов вычислите по 30 магазинам торговой ассоциации: среднегодовую стоимость основных фондов, приходящую на один магазин; дисперсию и среднеквадратическое отклонение; коэффициент вариации; моду и медиану.
Решение задачи оформите в таблице.
4.7. Имеются данные о работе двух цехов завода:
Определите среднее линейное отклонение
Тема №5. «Индексный метод» Практическое занятие №1. Контрольные вопросы 1. Что такое сложная статистическая совокупность? 2. Перечислите признаки классификации и виды индексов. 3. Какие индивидуальные индексы вам известны? 4. Как рассчитать индивидуальный индекс физического объема? 5. В чем сущность соизмерителя в агрегатной форме общего индекса? 6. Как определяется общий индекс цен Пааше? 7. Что характеризует разность числителя и знаменателя общего индекса цен Пааше. 8. Охарактеризуйте сводный индекс физического объема. 9. Что представляет собой агрегатный индекс товарооборота? 10. Анализ влияния изменения товарооборота под влиянием воздействия различных факторов. 11. Что такое индекс переменного состава? 12. В чем сущность средневзвешенных индексов? 13. Индекс постоянного состава и индекс влияния структурных сдвигов. 14. Взаимосвязь общих индексов. 15. Когда используются средние арифметические и гармонические индексы?
Решение типовых задач Пример 5.1. Имеются следующие данные о реализации овощной продукции на овощном рынке:
Рассчитайте индивидуальные индексы цен, физического объёма и товарооборота. Решение: Для расчета индивидуальных индексов используем формулы: - индекс цен - индекс физического объема - индекс товарооборота Расчеты выполним в таблице. Дополним таблицу – условие столбцами:
Контроль Для проверки правильности решения задачи воспользуемся формулой связи индексов: 1) картофель: 2) капуста: 3) морковь: Ответ: 1) индивидуальные индексы цен показывают, что цена на картофель снизилась на 30%, на капусту – на 50%, а цена на морковь не изменилась в отчётном периоде по сравнению с базисным; 2) индивидуальные индексы физического объема показывают, что количество проданного картофеля увеличилось на 26,7%; продажа капусты увеличилась на 100%, т.е. возросла в 2 раза, а моркови – в 1,5 раза или на 50% в октябре месяце по сравнению с августом; 3) индивидуальные индексы товарооборота показывают, что товарооборот картофеля снизился на 11,3%, капусты – не изменился, а моркови увеличился в 1,5 раза или на 50% в отчетном периоде по сравнению с базисным периодом.
Пример 5.2. Имеются следующие данные о реализации овощной продукции на овощном рынке:
Определите: 1. Общие (агрегатные) индексы цен, физического объема и товарооборота; 2. Экономию или перерасход денежных средств населения в результате изменения цен на товары в отчетном периоде по сравнению с базисным Решение: Для расчета агрегатных индексов используем формулы: индекс цен (Пааше) Расчеты выполним в таблице. Дополним таблицу – условие столбцами:
На основании полученных данных находим: 1) агрегатный индекс цен Пааше 2) агрегатный индекс физического объема 3) агрегатный индекс товарооборота 4) Для ответа на вопрос об экономии или перерасходе денежных средств населением воспользуемся индексом цен: Итак, находим
Задачи для самостоятельного решения 5.1.
Определите: 1) Общие (агрегатные) индексы цен, физического объема и товарооборота. 2) Экономию или перерасход денежных средств населения в результате изменения цен на товары в отчетном периоде по сравнению с базисным.
5.2. Имеются данные о товарообороте продовольственных товаров в одном из магазинов:
Определите: 1) индивидуальные и общие индексы физического объема, 2) индивидуальные и общий индексы цен, 3) сумму перерасхода (или экономии) населения от изменения цен во II –ром периоде при покупке данных товаров.
5.3. Имеются следующие данные о выпуске продукции «А» по двум заводам города:
Определите индексы себестоимости продукции: 1) переменного состава; 2) фиксированного состава; 3) влияния структурных сдвигов; 4) изменение средней себестоимости (в абсолютных величинах в отчетном году по двум заводам в целом и за счет действия отдельных факторов).
5.4. Как изменилось количество реализованных товаров, если и цены, и товарооборот увеличились на 10%?
5.5. Затраты на производство продукции увеличились на 10%, количество произведенной продукции возросло на 7%. Как изменилась в среднем себестоимость произведенной продукции?
5.6. Известно, что индекс постоянного состава равен 102,5%, а индекс структурных сдвигов – 100,6%. Определите индекс переменного состава.
5.7. Имеются следующие данные:
Определите: 1) общий индекс физического объема реализации; 2) общий индекс цен, если известно, что товарооборот в марте по сравнению с февралем увеличился на 12%.
5.8. Выручка фирмы от реализации товара на рынке выросла на 10% при увеличении объёма продажи товара на 22%. Как изменились цены на товар? Практическое занятие №2. Выполнение аудиторной контрольной работы № 1
Тема №6. «Выборочный метод» Практическое занятие №1.
Контрольные вопросы 1. В чем состоит выборочный метод? 2. Преимущества выборочного метода по сравнению другими несплошными методами наблюдения. 3. Ошибки репрезентативности. 4. Что такое доверительная вероятность и уровень значимости? Как они связаны между собой? 5. Сформулируйте принцип практической уверенности. 6. Доверительный интервал. 7. Запишите, по какой формуле вычисляется предельная ошибка в случае малой выборки и в случае большой выборки. 8. Классификация выборок. 9. Расчет предельных ошибок в случае механического отбора. 10. Расчет предельных ошибок в случае собственно-случайного отбора
Решение типовых задач Пример 7.1. При случайном повторном отборе было установлено, что средний вес товара в выборочной совокупности, состоящей из 90 изделий, оказался равным 8,2 кг при среднем квадратическом отклонении 0,5 кг. С вероятностью, равной 0,954, определите, в каких пределах заключен средний вес товара в генеральной совокупности. Решение: Найдём
Доверительный интервал: Ответ: средний вес товара с надежностью 0,954 заключен в диапазоне
Пример 7.2. В результате выборочного обследования 55 сотрудников банка, общее количество которых составляет 140 человек, осуществленного на основе бесповторного отбора, были получены следующие данные:
Определить доверительный интервал средней выслуги лет сотрудников банка (доверительная вероятность 0,954). Решение: Рассчитаем среднюю выслугу лет:
Выборочная средняя равна:
Дисперсия равна:
Предельная ошибка выборки:
Округление предельной ошибки дает значение 1,5. Доверительный интервал генеральной средней:
Таким образом, на основании приведенного выборочного обследования с вероятностью 0,954 можно заключить, что средняя выслуга лет сотрудников банка лежит в пределах от 11,6 до 14, 6 лет.
Задачи для самостоятельного решения 7.1. При случайном повторном отборе было установлено, что средний вес товара в выборочной совокупности, состоящей из 120 изделий, оказался равным 9 кг при среднем квадратическом отклонении 0,25 кг. С вероятностью, равной 0,95, определите, в каких пределах заключен средний вес товара в генеральной совокупности. 7.2. Произведено шесть независимых измерений толщины пластины. Получены следующие результаты: 2,15; 2,18; 2,14; 2,16; 2,17; 2,15. Оценить истинное значение толщины пластины с помощью доверительного интервала с доверительной вероятностью 0,95. 7.3. Результаты исследования длительности оборота оборотных средств торговых фирм города (в днях) представлены в группированном виде:
Построить доверительный интервал на уровне значимости 0,05 для средней длительности оборота оборотных средств торговых фирм города. (Принять, что выборка осуществлялась бесповторным методом) 7.4. В одном из лесничеств Рязанской области методом случайной бесповторной выборки обследовано 1000 деревьев с целью установленья их среднего диаметра, который оказался равным 210 мм при 7.5. На складе магазина насчитывается 50 телевизоров. Отобрано 6 телевизоров с целью контроля некоторых параметров. Результаты измерения напряжения 7.6. В порядке механической выборки обследован возраст 100 студентов вуза из общего числа 2000 человек. Результаты обработки материалов наблюдения приведены в таблице:
Найдите: 1) средний возраст студентов вуза по выборке, 2) интервальную оценку возраста студентов (доверительная вероятность 0,95). 7.7. Для определения среднего возраста 600 студентов экономического факультета необходимо провести выборочное обследование механическим способом. Установлено, что среднее квадратическое отклонение возраста студентов равно 9 годам. Определите, сколько студентов нужно обследовать, чтобы с вероятностью 0,99 средняя ошибка выборки не превышала трех лет? 7.8. Численность сотрудников таможенного органа – 250 человек. С вероятностью, равной 0,954, определите, в каких пределах заключен средний размер денежного довольствия сотрудника таможенного органа. В порядке случайной бесповторной выборки было обследовано 50 человек. Средний размер денежного довольствия составил 53000 руб. при средним квадратическим отклонением 5650 руб. 7.9. Генеральная совокупность, распределенная по нормальному закону, изучается выборочным повторным методом по некоторому признаку Практическое занятие №2. Контрольные вопросы 1. Расчет стандартных ошибок в случае типического отбора. 2. Расчет предельных ошибок в случае механического отбора. 3. Расчет стандартных ошибок в случае серийного отбора. Решение типовых задач Пример 8.1. Для определения процента людей, нашедших себе супруга через брачное агентство, была организована случайная выборка, объем которой составлял 500 человек из обратившихся за помощью в брачное агентство. Среди них 75 нашли себе супруга. Найти 90 %-ный доверительный интервал, накрывающий неизвестный процент людей, нашедших себе супруга через брачное агентство. Решение: Доля человек нашедших себе супруга составляет Найдем доверительный интервал для оценки генеральной доли
Пример 8.2. В результате 20-ного бесповторного типического отбора, проведенного на трех предприятиях отрасли, пропорционально размеру предприятий получены следующие данные по оценке среднего размера заработной платы.
На основе приведенных данных определите пределы нахождения средней заработной платы одного рабочего по отрасли в целом. Решение: Рассчитаем среднюю из внутригрупповых дисперсий:
Определим предельную ошибку выборки с вероятностью 0,954 (
Рассчитаем выборочную среднюю:
С вероятностью 0,954 можно сделать вывод, что средняя заработная плата одного рабочего в целом по отрасли находится в пределах:
Пример 8.3. В результате 50 %-ного бесповторного серийного отбора, проведенного в четырех из восьми строительных бригад, получены следующие данные по оценке стажа работы строителей.
Найдите доверительный интервал среднего стажа работы одного строителя с вероятностью 0,954. Решение: Рассчитаем выборочную среднюю:
Рассчитаем межгрупповую дисперсию:
Вычислим предельную ошибку:
С вероятностью 0,954 можно сделать вывод, что средний стаж работы одного строителя в целом по всему предприятию находится в пределах:
Задачи для самостоятельного решения 8.1. Из партии, содержащей 8000 телевизоров, отобрано 800. Среди них оказалось 10% не удовлетворяющих стандарту. Найти границы, в которых с вероятностью 0,95 заключена доля телевизоров, удовлетворяющих стандарту во всей партии для повторной и бесповторной выборок. 8.2. По результатам социологического обследования при опросе 1500 респондентов рейтинг президента (т.е. процент опрошенных, одобряющих его деятельность) составил 30%. Найти границы, в которых с надежностью 0,95 заключен рейтинг президента (при опросе всех жителей страны). Сколько респондентов надо опросить, чтобы с надежностью 0,99 гарантировать предельную ошибку социологического обследования не более 1%? 8.3. Фирма решила открыть ювелирный магазин в новом районе города и хотела бы оценить долю людей, заинтересованных в изделиях магазина. Компания хотела бы знать оценку генеральной доли с предельной вероятностью 0,99. Для этого предполагается провести опрос жителей района. По опыту предыдущих опросов компания может считать, что генеральная доля колеблется около 0,25. Чему равен необходимый объем выборки для оценки генеральной доли? 8.4. В процессе технического контроля из партии готовой продукции методом случайного бесповторного отбора было проверено 80 изделий, из которых четыре оказались бракованными. Можно ли с вероятностью 0,954 утверждать, что доля бракованных изделий во всей партии не превышает 7 %, если процент отбора равен 10? 8.5. Для контроля всхожести партии семян была разбита на 25 равных по величине серий. Затем на основе случайного бесповторного отбора было проверено на всхожесть 5 серий. В результате установлено, что процент всхожести семян составляет 68. Межсерийная дисперсия равна 0,04. Определите с вероятностью 0,9 пределы, в которых находится доля взошедших семян. 8.6. В коммерческом банке 160 персональных компьютеров четырех типов, в том числе типа А – 32, типа Б – 48, типа В – 64, типа Г – 16. Для изучения эффективности их использования предполагается организовать выборочное обследование на основе типической пропорциональной выборки. Отбор внутри типов – механический. Определите, какое количество компьютеров необходимо отобрать, чтобы с вероятностью 0,9 ошибка не превышала пяти единиц. По материалам предыдущего обследования известно, что дисперсия типической выборки равна 729.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 2137; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 , га
, га
 , согласно условию
, согласно условию  ,
,  , тогда
, тогда 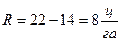 .
. ,
,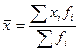 – средняя урожайность пшеницы.
– средняя урожайность пшеницы. ,
, ,
, ,
, .
.




 .
. .
. .
. – среднее квадрата,
– среднее квадрата,  – квадрат средней. Для вычисления суммы
– квадрат средней. Для вычисления суммы  дополним расчётную таблицу столбцом
дополним расчётную таблицу столбцом  и заполним его.
и заполним его. .
. .
.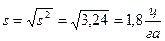




 для каждого цеха.
для каждого цеха.


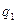
 , где р 1 - цена в отчетном периоде, р 0 – цена в базисном периоде.
, где р 1 - цена в отчетном периоде, р 0 – цена в базисном периоде. , где
, где  – физический объем в базисном периоде.
– физический объем в базисном периоде. , где
, где  – товарооборот в отчетном периоде;
– товарооборот в отчетном периоде; 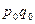 – товарооборот в базисном периоде.
– товарооборот в базисном периоде.
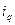

 .
.

 , таким образом, расчеты выполнены правильно
, таким образом, расчеты выполнены правильно , индекс физического объема
, индекс физического объема  , индекс товарооборота
, индекс товарооборота  , где
, где  – товарооборот в отчётном периоде по ценам базисного.
– товарооборот в отчётном периоде по ценам базисного. или 68, 28%, т.е. средняя цена рассматриваемой товарной группы снизилась в октябре на 31,72% (68,28%-100%);
или 68, 28%, т.е. средняя цена рассматриваемой товарной группы снизилась в октябре на 31,72% (68,28%-100%);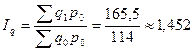 или 145,2%, т.е. объём продаж по данной товарной группе в среднем увеличился на 45,2% (145,2%-100%);
или 145,2%, т.е. объём продаж по данной товарной группе в среднем увеличился на 45,2% (145,2%-100%);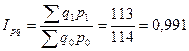 или 99,1%, в целом по рассматриваемой товарной группе в текущий период товарооборот снизился на 0,9% (99,1%-100%)
или 99,1%, в целом по рассматриваемой товарной группе в текущий период товарооборот снизился на 0,9% (99,1%-100%)

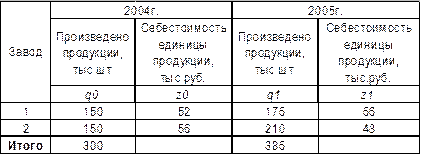

 . Из отношения
. Из отношения  получим
получим  . По таблице находим
. По таблице находим  . Предельная ошибка равна:
. Предельная ошибка равна: Округление дает значение предельной ошибки
Округление дает значение предельной ошибки 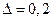 .
. ,
, 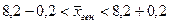 ,
,  .
.



 лет.
лет.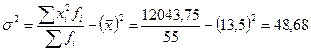 лет2
лет2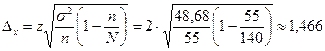




 126 мм. С вероятностью 0,9 определите пределы среднего диаметра деревьев в генеральной совокупности (считать, что n<<N).
126 мм. С вероятностью 0,9 определите пределы среднего диаметра деревьев в генеральной совокупности (считать, что n<<N). источника питания в телевизорах: 12; 11,5; 12,2; 12,5; 12,3 и 12,1 В. Найти интервальную оценку параметра
источника питания в телевизорах: 12; 11,5; 12,2; 12,5; 12,3 и 12,1 В. Найти интервальную оценку параметра  . Какой объем выборки будет гарантировать, что предельная ошибка не превысит значения 3,5 с вероятностью 0,95?
. Какой объем выборки будет гарантировать, что предельная ошибка не превысит значения 3,5 с вероятностью 0,95? .
. с надежностью 0,9:
с надежностью 0,9:  . Сначала рассчитаем предельную ошибку по формуле:
. Сначала рассчитаем предельную ошибку по формуле:  . Из таблицы функции Гаусса определяем
. Из таблицы функции Гаусса определяем  .
.  .
. ,
,  .
. .
.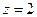 ):
): .
. .
.

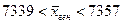


 .
.
 .
.


