
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вспомогательные расчеты показателей вариации разряда рабочихСодержание книги
Поиск на нашем сайте
2. Общую дисперсию тарифного разряда рабочих определим по формуле для сгруппированных данных:
При этом распределение рабочих на группы учитывать не будем, так как общая дисперсия рассчитывается по всей совокупности рабочих – 72 чел. От каждого тарифного разряда (графа 1) отнимаем общий средний разряд – 3,47 и записываем разность в графу 4, а затем эту разность возводим в квадрат и умножаем на соответствующее число рабочих ( графа 4 графа 5
Общая дисперсия характеризует вариацию тарифного разряда рабочих, возникающую под влиянием стажа работы (группировочного признака), так и прочих неучтенных факторов. 3. Межгрупповую дисперсию тарифного разряда определяем как средний квадрат, средних групповых и среднего общего разряда:
Межгрупповая дисперсия характеризует вариацию тарифного разряда рабочих, которая возникает вследствие вариации стажа работы (группировочного признака). 4. При расчете дисперсии каждой отдельной группы исходим из того, что каждая группа имеет свое значение среднего тарифного разряда, определенное в п. 1. Вспомогательные расчеты для групповых дисперсий проведем в таблице, графы 6 и 7. Так, в первой середине рабочих по стажу средний тарифный разряд составляет 2,78. Тогда в первой строке: в графе 6 разность « Групповая дисперсия рассчитывается по формуле:
и для первой группы равна:
Аналогичные расчеты проводим по 2-ой и 3-ей группам рабочих, но с учетом среднего тарифного разряда соответственно 3,57 и 4,41. Дисперсия разряда рабочих: второй группы:
третьей группы:
Далее определяем среднюю из групповых дисперсий:
Средняя из групповых дисперсий показывает вариацию тарифного разряда рабочих, которая возникает под влиянием прочих факторов, кроме стажа работы (группировочного фактора). Проверка правила сложений дисперсий:
Небольшое расхождение (0,11) объясняется округлением результатов практически всех расчетов. 5. Коэффициент детерминации:
Вывод: вариация тарифного разряда рабочих на 54% зависит от вариации стажа работы (факторного признака) и на 46% – от всех остальных условий, действующих в данной совокупности.
Эмпирическое корреляционное отношение:
Теснота связи между тарифным разрядом рабочих и стажем работы достаточно высокая, стремится к 1.
Тема 8. Выборочное наблюдение
Цель: Обосновать необходимость выборочного наблюдения, разъяснить его суть, способы отбора, ошибки.
План: 1. Понятие выборочного исследования, его сущность и применение на практике 2. Виды и способы, обеспечивающие репрезентативность выборочной совокупности 3. Определение ошибок выборочного наблюдения. Расчет относительной ошибки выборки 4. Методы распространения характеристик выборочных показателей на генеральную совокупность 5. Расчет необходимой численности выборочной совокупности
Понятие выборочного исследования, его сущность И применение на практике
Выборочный метод в статистике дает возможность путем исследования ограниченного числа единиц совокупности судить обо всей (генеральной) совокупности. Т.е. сущность выборочного наблюдения состоит в том, что обследованию подвергается часть совокупности, отобранная по особым правилам. Повышение внимания к выборочному наблюдению в настоящее время связано с необходимостью более оперативного реагирования на происходящие изменения, позволяет принимать своевременные решения, что особенно важно в условиях рынка. Выборочное наблюдение – это статистическое наблюдение, позволяющее экономить время и средства, которые были бы затрачены на проведение сплошного наблюдения, предупреждает порчу и даже уничтожение объектов, посредством его можно уточнить результаты сплошного наблюдения. К важнейшим видам выборочных наблюдений относятся: - демографические обследования (например, выборочное обследование доходов и расходов домашних хозяйств); - социологические обследования, опросы; - проверка качества готовой продукции, особенно при разрушительных методах контроля; - определение потерь рабочего времени путем проведения моментных наблюдений или фотографии рабочего дня и другие.
При организации выборочного наблюдения надо помнить, что оно не сплошное, но должно быть достаточно массовым, чтобы обеспечить определенную вероятность обобщающих показателей для характеристики совокупности в целом. Поэтому при формировании выборочной совокупности необходимо соблюдать принципы случайного отбора: а) каждая единица генеральной совокупности должна иметь равную возможность попадания в выборку, т.е. должен действовать принцип случайного непредвзятого отбора; б) в выборочную совокупность должны попасть представители всех групп, имеющихся в генеральной совокупности; в) выборочная совокупность должна по основным показателям полно и адекватно воспроизводить закономерности, присущие всей генеральной совокупности. Это значит, что выборочная совокупность должна быть репрезентативной (представительной).
Совокупность, из которой производится отбор, называется генеральной совокупностью; отобранные данные представляют выборочную совокупность или выборку. В теории выборочного метода используются следующие обозначения:
Выборочная доля, или частость, w определяется из отношения единиц, обладающих изучаемым признаком m, к общей численности единиц выборочной совокупности n:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 423; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.83.149 (0.009 с.) |




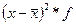

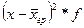
 .
. ), результат показываем в графе 5. Так, по строке этот расчет имеет вид:
), результат показываем в графе 5. Так, по строке этот расчет имеет вид:

 .
. ;
;
 » составит 0,78 (2 – 2,78); в графе 7расчет производим как
» составит 0,78 (2 – 2,78); в графе 7расчет производим как  и т.д.
и т.д.

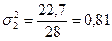 ;
; .
. ;
; .
. ;
; .
. ;
;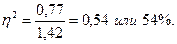
 ;
; .
.

 . (8.1)
. (8.1)


