
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет аналитических показателей динамикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Абсолютный прирост ( а) базисный (
б) цепной (
где 2. Темп роста ( а) базисный (
б) цепной (
3. Темп прироста ( а) базисный (
б) цепной (
Между показателями темпа роста и прироста существует взаимосвязь: темп прироста всегда на единицу меньше темпа роста, выраженного в коэффициентах и на 100% меньше темпа роста, выраженного в %:
4. Ускорение: а) абсолютное (
Отрицательное значение показателя говорит о замедлении роста. Ускорение, равное нулю, характеризует прямолинейную тенденцию. Постоянное ускорение характеризует параболическую тенденцию; б) относительное (
5. Темп наращивания (
6. Абсолютное значение одного процента прироста (К1 %) – это отношение абсолютного прироста к темпу прироста, выраженного в процентах. Иначе его можно получить делением значения предыдущего уровня ряда на 100:
Абсолютное значение одного процента прироста показывает, на сколько весом каждый % прироста, какое содержание за ним скрывается. Между показателями динамики, вычисленными по базисному и цепному методам с постоянной и переменной базой, существует определенная связь:
Если известны: цепные темпы роста, то базисные находятся путем их последовательного умножения, а если известны базисные, то чтобы найти цепной, надо последующий базисный разделить на предыдущий:
где
Пример 4. По данным о численности населения города рассчитайте аналитические показатели динамики (табл. 9.4). Таблица 9.4 Численность населения города
Средние показатели динамики
Средний уровень ряда динамики – характеризует типическую величину абсолютных уровней. Он рассчитывается: 1. в интервальном ряду по средней арифметической простой:
2. в моментном динамическом ряду с равными промежутками времени между датами – по средней хронологической:
где 3. в моментом ряду с неравными промежутками времени между датами – по средней арифметической взвешенной:
где
где
Пример 5. Определите среднегодовую численность населения каждого района по данным табл. 9.5.
Таблица 9.5
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 475; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.26.149 (0.007 с.) |

 ) – это разность значений двух уровней ряда динамики:
) – это разность значений двух уровней ряда динамики: ) – исчисляется как разность между сравниваемым уровнем ряда yi и уровнем, принятым за постоянную базу сравнения yo:
) – исчисляется как разность между сравниваемым уровнем ряда yi и уровнем, принятым за постоянную базу сравнения yo: ; (9.1)
; (9.1) ) – это разность между сравниваемым уровнем ряда yi и уровнем, ему предшествующим yi-1:
) – это разность между сравниваемым уровнем ряда yi и уровнем, ему предшествующим yi-1: , (9.2)
, (9.2) – значение показателя в i-ом периоде;
– значение показателя в i-ом периоде;  – значение показателя в предшествующем i-1 периоде;
– значение показателя в предшествующем i-1 периоде;  – значение показателя в базисном периоде.
– значение показателя в базисном периоде. ) – это отношение двух уровней ряда. Может выражаться в виде коэффициента или в процентах:
) – это отношение двух уровней ряда. Может выражаться в виде коэффициента или в процентах: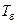 ) – исчисляется как отношение сравниваемого уровня ряда yi и уровня, принятого за постоянную базу сравнения y0:
) – исчисляется как отношение сравниваемого уровня ряда yi и уровня, принятого за постоянную базу сравнения y0: ; (9.3)
; (9.3) ) – исчисляется как отношение сравниваемого уровня ряда yi и уровня, ему предшествующего yi-1:
) – исчисляется как отношение сравниваемого уровня ряда yi и уровня, ему предшествующего yi-1: . (9.4)
. (9.4) ) – это отношение абсолютного прироста к сравниваемому уровню. Он характеризует абсолютный прирост в относительных величинах:
) – это отношение абсолютного прироста к сравниваемому уровню. Он характеризует абсолютный прирост в относительных величинах: ) – исчисляется как отношение абсолютного базисного прироста
) – исчисляется как отношение абсолютного базисного прироста  и уровня, принятого за постоянную базу сравнения y0:
и уровня, принятого за постоянную базу сравнения y0: ; (9.5)
; (9.5) ;
; ) – исчисляется как отношение цепного прироста
) – исчисляется как отношение цепного прироста  и уровня, ему предшествующего yi-1:
и уровня, ему предшествующего yi-1: ; (9.6)
; (9.6) .
.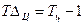 ; (9.7)
; (9.7) ; (9.8)
; (9.8) .
. ) – разность между абсолютным изменением за данный период и абсолютным приростом за предшествующий период равной длительности. Измеряется показатель только в цепном варианте:
) – разность между абсолютным изменением за данный период и абсолютным приростом за предшествующий период равной длительности. Измеряется показатель только в цепном варианте: . (9.10)
. (9.10) ) – это отношение двух цепных темпов прироста – последующего к предыдущему:
) – это отношение двух цепных темпов прироста – последующего к предыдущему: . (9.11)
. (9.11) ) – это отношение цепных абсолютных приростов к уровню, принятому за постоянную базу сравнения:
) – это отношение цепных абсолютных приростов к уровню, принятому за постоянную базу сравнения: (9.12)
(9.12) . (9.13)
. (9.13) . (9.14)
. (9.14) , (9.15)
, (9.15) – произведение.
– произведение.


 =
=  ; (9.16)
; (9.16) , (9.17)
, (9.17) – количество моментов времени, на которые зафиксированы значения показателя (
– количество моментов времени, на которые зафиксированы значения показателя ( ).
). (9.18)
(9.18) – величина промежутка времени между двумя датами;
– величина промежутка времени между двумя датами;  – среднее значение признаков на каждом i-м промежутке, рассчитывается по формуле средней арифметической простой:
– среднее значение признаков на каждом i-м промежутке, рассчитывается по формуле средней арифметической простой: , (9.19)
, (9.19) – значения признака соответственно в начале и в конце интервала.
– значения признака соответственно в начале и в конце интервала.


