
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведение рядов динамики к одному основаниюСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Из данных таблицы видно, что среднемесячная выработка и заработная плата рабочего увеличиваются, однако разная размерность и разный исходный уровень этих показателей не позволяют определить, уровень какого из них изменяется более быстрыми темпами. В этой связи оба динамических ряда приводят к одному основанию, приняв в качестве базы сравнения начальный уровень ряда. Из расчета видно, что среднемесячная выработка увеличивается более быстрыми темпами, чем среднемесячная заработная плата. 4. Чтобы представить количественную модель, выражающую общую тенденцию изменений уровней динамического ряда во времени используется аналитическое выравнивание ряда динамики. В этом случае фактические уровни заменяются уровнями, вычисленными на основе определенной кривой. Предполагается, что она отражает общую тенденцию изменения во времени изучаемого показателя. При аналитическом выравнивании ряда динамики закономерно изменяющийся уровень изучаемого показателя оценивают как функцию времени Таблица 9.8 Виды трендовых моделей
и т.д. Определение расчетных уровней уt производится на основе адекватной математической функции, наилучшим образом отображающей основную тенденцию ряда динамики. Подбор функции осуществляется методом наименьших квадратов. Суть его состоит в том, что эмпирические уровни ряда
Аналитическое выравнивание по прямой линии производится в том случае, если наблюдается равномерный абсолютный прирост.
Уравнение имеет вид:
где Для определения параметров
Решение можно упростить, если
Пример 8. Произвести выравнивание по прямой линии (табл. 9.10). Таблица 9.10 Данные о строительстве жилья
Используя итоги граф 2, 4 и 5 определим параметры уравнения прямой:
По рассчитанным параметрам записываем уравнение прямой ряда динамики, характеризующее строительство жилья:
Рассчитываем для каждого года теоретические значения, исходя из уравнения: для 2003г. для 2004г. Правильность расчета уровней выравниваемого ряда динамики может быть проверена следующим образом: сумма значений эмпирического ряда должна совпадать с суммой вычисленных уровней выровненного ряда, т.е.
Продление в будущее тенденции, наблюдавшейся в прошлом, носит название экстраполяции. Экстраполируя при Если для уравнения тренда подходят одновременно несколько функций, то отбор оптимальной производится по величине стандартизированной ошибки аппроксимации, которая вычисляется по формуле:
Аппроксимация – это приближенное выражение одних функций другими. Чем меньше величина стандартизированной ошибки Используя данные примера 8, рассчитаем среднюю квадратическую ошибку линейного тренда:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 490; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.225.254 (0.01 с.) |

 , где
, где  – уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени
– уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени  . В таблице 9.8 приведены различные виды трендовых моделей, наиболее часто используемые для аналитического выравнивания.
. В таблице 9.8 приведены различные виды трендовых моделей, наиболее часто используемые для аналитического выравнивания.


 заменяются плавной линией выровненных уровней
заменяются плавной линией выровненных уровней  таким образом, чтобы сумма квадратов этих отклонений была равна 0.
таким образом, чтобы сумма квадратов этих отклонений была равна 0. . (9.23)
. (9.23) , (9.24)
, (9.24) – свободный параметр (если
– свободный параметр (если  , то
, то  );
);  – параметр динамики, показывающий как в среднем изменится
– параметр динамики, показывающий как в среднем изменится  , если
, если  .
. , тогда:
, тогда: ; (9.25)
; (9.25) . (9.26)
. (9.26)




 ;
; .
. .
.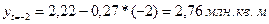 ,
, и т.д.
и т.д. (см. итоги граф 2 и 6).
(см. итоги граф 2 и 6). , находим уровень 2008г.
, находим уровень 2008г.  .
. . (9.27)
. (9.27) , тем лучше уравнение тренда отражает тенденцию развития.
, тем лучше уравнение тренда отражает тенденцию развития. млн. кв. м
млн. кв. м


