
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды и способы, обеспечивающие репрезентативностьСодержание книги
Поиск на нашем сайте
Выборочной совокупности
Чтобы выборка полно и адекватно представляла свойства генеральной совокупности, она должна быть представительной, т.е. репрезентативной. Репрезентативность может быть обеспечена только при объективности отбора данных. Возможны следующие виды отбора единиц для формирования выборочной совокупности: 1) собственно-случайный отбор; 2) механический отбор; 3) типическая выборка; 4) серийная выборка.
Собственно-случайная (непреднамеренная) выборка – при этом выборочная совокупность образуется с помощью жеребьевки или таблицы случайных чисел. Условием репрезентативности случайной выборки является то, что каждая единица имеет равную возможность попадания в выборку. Сам отбор может быть повторным и бесповторным. При повторном отборе вероятность попадания каждой отдельной единицы в выборку остается постоянной, т.к. после отбора отобранная единица возвращается в совокупность и снова может быть выбранной – это «возвратного шара». При бесповторном отборе отобранная единица не возвращается обратно, вероятность попадания остающихся единиц в выборку все время меняется – это «схема безвозвратного шара». Механический отбор – при этом выборочная совокупность определяется из генеральной, разбитой на равные интервалы (группы). Размер интервала равен обратной величине доли выборки: так, при 5% выборке отбирается каждая 20-я единица (1:0,05). Для обеспечения репрезентативности все единицы генеральной совокупности должны располагаться в определенном порядке (возрастающем / убывающем). При этом отбор осуществляется через определенный интервал. Типическая (расслоенная, стратифицированная) выборка – предполагает предварительную разбивку генеральной совокупности на качественно однородные типические группы (не обязательно равные). Затем отбор в выборочную совокупность из генеральной производится из типических групп при помощи собственно-случайного или механического отбора пропорционально объему данной группы. Типическая выборка обычно применяется при изучении сложных статистических совокупностей. Она дает более точные результаты по сравнению с другими способами отбора. Серийная (гнездовая) выборка – при этом генеральная совокупность разбивается на серии, и отбираются не отдельные единицы, а серии. Внутри каждой из попавшей в выборку серии обследуются все без исключения единицы.
Определение ошибок выборочного наблюдения. Расчет относительной ошибки выборки
При использовании выборочного метода возникает так называемая ошибка репрезентативности – это расхождение между характеристиками выборки и генеральной совокупности. Она зависит от численности выборки, вариации признака, методов отбора единиц выборочной совокупности и т.д. Ошибка может быть рассчитана по формуле:
При
Ошибка репрезентативности является результатом того, что выборочная совокупность не полностью отражает закономерности, присущие всей генеральной совокупности. Методы математической статистики дают возможность измерить эту ошибку и указать границы ее колеблемости. Ошибки репрезентативности: 1. Систематические – в случае нарушения научного принципа отбора единиц в выборочную совокупность. 2. Случайные – это неточности, возникающие из-за того, что выборочная совокупность не совсем правильно воспроизводит структуру генеральной совокупности. С увеличением численности выборки величина выборочной средней будет приближаться к генеральной средней. Рассчитывают два вида ошибок: - среднюю ( - предельную (
Под средней ошибкой выборки понимают такое расположение между средней выборочной Расчет средней ошибки представлен в табл. 8.1. Таблица 8.1. Расчет средней ошибки
Порядок расчета ошибок выборки для средней: 1. По данным выборочного наблюдения устанавливается величина выборочной средней ( 2. Определяется средняя ошибка выборки: а) для повторного отбора:
б) для бесповторного отбора (согласно исходным данным):
3. С заданной вероятностью P(t) находится предельная ошибка выборки – это максимально возможное расхождение (
где t – заданный коэффициент доверия (критерий кратности ошибки выборки);
Множитель t определяется в зависимости от того, с какой доверительной вероятностью P(t) надо гарантировать результаты выборочного наблюдения. На практике пользуются готовыми таблицами значений (табл. 8.2). Таблица 8.2
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 484; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.22.8 (0.008 с.) |

 ; (8.2)
; (8.2) . (8.3)
. (8.3) :
: ;
; .
. ) – стандартную;
) – стандартную; ).
). и средней генеральной совокупностью
и средней генеральной совокупностью  , которое не превышает
, которое не превышает  .
.
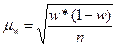 – дисперсия доли признака
– дисперсия доли признака


 ; (8.4)
; (8.4) ), т.е. максимум ошибки при заданной вероятности ее появления:
), т.е. максимум ошибки при заданной вероятности ее появления: , (8.6)
, (8.6) – предельная ошибка выборки.
– предельная ошибка выборки.


