
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средний арифметический и гармонический индексы,Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Тождественные агрегатному В ряде случаев из-за отсутствия некоторых данных нельзя произвести расчет по формуле агрегатного индекса. В этом случае применяют средние индексы. Проведем преобразование агрегатного индекса физического объема продукции в тождественную ему форму средних индексов. Для этого из формулы
Так общий индекс физического объема продукции может быть рассчитан как средняя арифметическая из индивидуальных индексов физического объема продукции, взвешенных по стоимости продукции базисного периода. Этот индекс получил название среднего арифметического индекса, тождественного агрегатному. Средняя гармоническая форма общего индекса физического объема продукции выглядит следующим образом: из индивидуального индекса физического объема выразим
Таким образом, общий индекс физического объема продукции может быть рассчитан как средняя гармоническая из индивидуальных индексов физического объема продукции, взвешенных по стоимости продукции отчетного периода. Этот индекс получил название среднего гармонического индекса, тождественного агрегатному. Пример приведен в табл. 10.3. Таблица 10.3 Имеются данные
Определим общий индекс физического объема продукции:
В тех случаях, когда нет данных о количестве проданных (произведенных) товаров, нельзя исчислить агрегатный индекс цен. Но если известны индивидуальные индексы цен и стоимостные объемы в текущем периоде в ценах этого периода, можно определить средний гармонический индекс цен. Агрегатный индекс цен:
Исходя из индивидуального индекса цен Таблица 10.4 Имеются данные
Определим общий индекс цены:
Измерение динамики среднего уровня с помощью Индексов постоянного, переменного состава и Структурных сдвигов
На динамику экономических явлений часто оказывает влияние изменение структуры изучаемой совокупности. Так, часто один и тот же вид продукции выпускают разные предприятия и по разным ценам. Тогда рассчитывают индексы средних величин. Они вычисляются только по качественным показателям, например: себестоимость, цена, производительность труда, заработная плата и т.д. по однородному кругу объектов.
Индексы средних величин представлены тремя видами: 1. Индексы переменного состава. 2. Индексы постоянного состава. 3. Индексы структурных сдвигов.
Расчет средних величин основан на формуле средней арифметической взвешенной:
Например, формулу средней цены можно представить следующим образом:
где
Изменение средней цены выражается индексом переменного состава:
Индекс, отражающий изменение средней цены в результате изменения индивидуальных цен на предприятиях при условии постоянства структуры совокупности (т.е. значения показателя, принимаемого в качестве весов, остаются неизменными на уровне отчетного периода), показывает индекс постоянного состава:
Индекс структурных сдвигов отражает изменение средней цены в результате изменения структуры продукции, при условии постоянства цен на продукцию:
Взаимосвязь индексов средних величин:
На основе данных индексов можно рассчитать абсолютное изменение средней цены изделия как в целом:
в том числе за счет изменения факторов: - в результате изменения индивидуальных цен на предприятиях при условии постоянства структуры выпуска (реализации) товаров:
- в результате изменения структуры совокупности:
Общее изменение средней цены равно:
Индексы средних величин взаимосвязаны: Расчет индексов средних величин приведен в табл. 10.5. Таблица 10.5
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 561; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.89.130 (0.011 с.) |

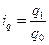 выразим
выразим 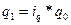 и подставим в числитель
и подставим в числитель 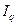 :
: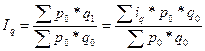 . (10.19)
. (10.19)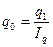 , подставим в знаменатель агрегатного индекса физического объема продукции:
, подставим в знаменатель агрегатного индекса физического объема продукции: . (10.20)
. (10.20)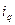
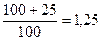
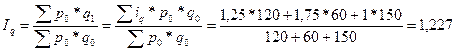 или 127%, т.е. объем продаж увеличился на 22,7%.
или 127%, т.е. объем продаж увеличился на 22,7%.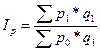 . (10.21)
. (10.21)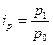 , определим
, определим  , тогда
, тогда 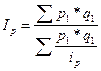 – это формула среднего гармонического индекса цен, тождественного агрегатному (пример расчета в табл. 10.4).
– это формула среднего гармонического индекса цен, тождественного агрегатному (пример расчета в табл. 10.4).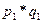 )
)
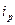
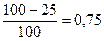
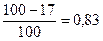

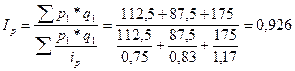 или 92,6%, т.е. цены снижены в среднем на 7,4%.
или 92,6%, т.е. цены снижены в среднем на 7,4%.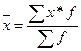 .
.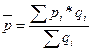 ,
,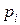 – цена товара i-го предприятия;
– цена товара i-го предприятия;  – объем производства товара в натуральном выражении соответствующего периода, т.е. это переменные веса.
– объем производства товара в натуральном выражении соответствующего периода, т.е. это переменные веса.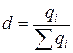 – структура производства (продаж) товара, доля.
– структура производства (продаж) товара, доля.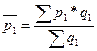 ;
; 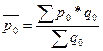 .
.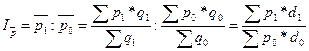 . (10.22)
. (10.22)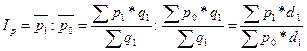 . (10.23)
. (10.23)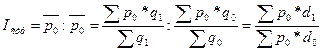 . (10.24)
. (10.24)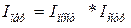 . (10.25)
. (10.25)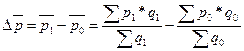 ; (10.26)
; (10.26)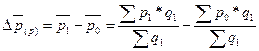 ; (10.27)
; (10.27)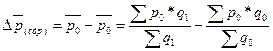 . (10.28)
. (10.28)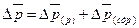 . (10.29)
. (10.29)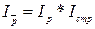 .
.


