Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Группировка рабочих по выработке продукцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определите абсолютные и относительные показатели вариации выработки продукции рабочими. Решение: Поскольку в условии группировка рабочих представлена в виде интервального вариационного ряда, предварительно надо определить середины интервалов ( Размах вариации составит:
Среднюю выработку по сгруппированным данным определяем по формуле средней арифметической взвешенной:
Среднее линейное отклонение:
Дисперсия выработки рабочих составит:
Среднее квадратическое отклонение равно:
Свойства дисперсии
Дисперсия имеет ряд математических свойств, которые могут быть использованы для упрощения ее расчета. 1. Если индивидуальные значения признака уменьшить или увеличить на некоторое постоянное число, то дисперсия не изменится.
2. Если индивидуальные значения признака разделить или умножить на некоторое постоянное число, то дисперсия соответственно уменьшится (увеличится) в квадрат от постоянного числа раз:
3. Дисперсия, рассчитанная от постоянной величины, больше дисперсии, рассчитанной от средней, на квадрат разности между средней величиной и постоянной:
4. Если постоянную величину приравнять к нулю, то дисперсия будет равна разности между средним квадратом значений признака и квадратом средней:
или
При
Дисперсия альтернативного признака
Наряду с вариацией количественных признаков, часто необходимо определить вариацию качественных или альтернативных признаков. Альтернативным называется признак, который может принимать только два значения: наступление или ненаступление события. На практике, например, изучается качество изготовленной продукции с помощью разделения ее на стандартную и бракованную. Условно считается, что альтернативный признак принимает значение, равное 1, если событие наступило, т.е. обследуемая единица обладает данным признаком, и равное 0, если событие не наступило. Удельный вес (доля) значений признака, для которых событие наступило, обозначим через, а для которых не наступило – через
Дисперсия альтернативного признака определяется по формуле:
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком, и доли единиц не обладающих данным признаком. Тогда среднее квадратическое отклонение альтернативного признака равно:
В случае, когда значения
Дисперсия альтернативного признака используется в выборочном наблюдении.
Пример 3. При приеме партии молока, фасованного в полимерные пакеты, в партии из 1000 пакетов двадцать имели дефекты упаковки. Определите дисперсию и среднее квадратическое отклонение доброкачественных пакетов молока.
Решение: Доля доброкачественных пакетов:
Доля дефектных пакетов:
Тогда:
Правило сложения дисперсий Дисперсия, как показатель вариации, может применяться в статистических рядах, где варианты совокупности сгруппированы по какому-либо признаку. Такой ряд состоит из признака-фактора (группированного) и признака-результата (результативного). Например, в качестве группированного признака для рабочих цеха могут выступать стаж работы, разряд (квалификация), в качестве результативного – выполнение норм выработки, средняя заработная плата. Для измерения колеблемости результативного признака под влиянием разных условий, действующих в данной совокупности, рассчитывают три дисперсии: – общую ( – межгрупповую ( – среднюю из групповых (
Общая дисперсия характеризует вариацию результативного признака под влиянием всех условий, действующих в данной совокупности. В зависимости от вида ряда, общую дисперсию определяют по формулам для несгруппированных или сгруппированных признаков. Межгрупповая дисперсия характеризует вариацию результативного признака под влиянием – признака-фактора, положенного в основу группировки:
где Для расчета средней из внутригрупповых дисперсий сначала определяют внутригрупповые дисперсии в каждой отдельной группе (
Средняя из внутригрупповых дисперсий, которая характеризует случайную вариацию результативного признака, т.е. вариацию под влиянием всех прочих факторов, кроме группированного, рассчитывается по формуле:
Поскольку общая колеблемость результативного признака определяется как колеблемость под влиянием группировочного признака и колеблемость под влиянием прочих факторов (кроме группировочного), то закономерно равенство:
Представленная формула – это правило сложения дисперсий: общая дисперсия равна сумме межгрупповой дисперсии и средней из групповых. На основе этих дисперсий можно рассчитать эмпирическое корреляционное отношение и коэффициент детерминации (причинности). Эмпирическое корреляционное отношение (
Оно изменяется то 0 до 1, и чем его значение ближе к 1, тем связь между признаками теснее. Коэффициент детерминации (причинности) (
Если межгрупповая дисперсия равна 0 (
Рассмотрим определение разных видов дисперсий на примере 4. Пример 4. Рабочие цеха сгруппированы по стажу работы в три группы. Со стажем работы связана квалификация рабочих (тарифный разряд). Данные представлены в табл. 7.3. Таблица 7.3 Таблица группировка рабочих по стажу работы
Определите: 1. средний разряд рабочих в каждой группе и по трем группам вместе; 2. общую дисперсию тарифного разряда; 3. межгрупповую дисперсию тарифного разряда; 4. групповые дисперсии и среднюю из групповых; 5. коэффициент детерминации, эмпирическое корреляционное отношение. Объясните смысл каждой дисперсии. Проверьте правило их сложения. Решение: 1. Поскольку мы имеем дело со сгруппированными данными, отметим элементы ряда: варианты (
Расчет среднего тарифного разряда: по 1-ой группе:
по 2-ой группе:
по 3-ей группе:
Средний тарифный разряд по всей совокупности рабочих составит:
Расчеты средних тарифных разрядов удобно выполнить во вспомогательной таблице, графа 3. В этой же таблице подготовим сведения для расчета дисперсий.
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 475; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.165.235 (0.006 с.) |





 ;
;



 ;
;  . (7.14)
. (7.14)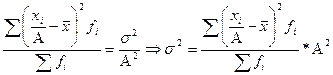 ;
;  . (7.15)
. (7.15) ;
;  . (7.16)
. (7.16) (7.17)
(7.17) . (7.18)
. (7.18)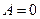 получим:
получим: . (7.19)
. (7.19)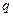 :
: . (7.20)
. (7.20) . (7.21)
. (7.21) . (7.22)
. (7.22)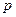 и
и  ;
;  . Тогда дисперсия будет равна:
. Тогда дисперсия будет равна: .
. .
. .
. .
. .
. );
);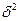 );
); ).
). , (7.23)
, (7.23) ) по формуле:
) по формуле: . (7.24)
. (7.24) . (7.25)
. (7.25) . (7.26)
. (7.26) ) показывает тесноту вязи между факторным и результативным признаками и рассчитывается по формуле:
) показывает тесноту вязи между факторным и результативным признаками и рассчитывается по формуле: . (7.27)
. (7.27) ) характеризует долю вариации результативного признака под влиянием признака-фактора, положенного в основу группировки. Формула расчета:
) характеризует долю вариации результативного признака под влиянием признака-фактора, положенного в основу группировки. Формула расчета: . (7.28)
. (7.28) ), это означает, что и коэффициент детерминации равен 0, следовательно, связь между факторным и результативным признаками полностью отсутствует. Полная связь между этими признаками (
), это означает, что и коэффициент детерминации равен 0, следовательно, связь между факторным и результативным признаками полностью отсутствует. Полная связь между этими признаками ( ) будет в случае равенства общей и межгрупповой дисперсий (
) будет в случае равенства общей и межгрупповой дисперсий ( ).
). .
.