
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гармонический состав выпрямленного напряженияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Во всех электрических цепях, содержащих полупроводниковые устройства, напряжение и ток чаще всего имеют несинусоидальную форму. Это является основой рабочего процесса самого устройства. Выпрямленное напряжение ud можно представить в виде двух составляющих: постоянной, т.е. значения Ud, и переменной
Несинусоидальная функция является периодической, если она удовлетворяет условию Поэтому составляющая
или где m – число пульсаций в выпрямленном напряжении за один период фазного напряжения источника Т; ν – номер гармонической составляющей выпрямленного напряжения;
Значения частот гармонических составляющих выпрямленного напряжения
Например, для частоты напряжения источника f1=50Гц частота первой гармонической выпрямленного напряжения - 100 Гц для однофазной мостовой схемы (m=2); - 300 Гц для трехфазной мостовой схемы (m=6). Действующее значение напряжения ud равно
где Амплитуда ν-ой гармонической составляющей выпрямленного напряжения для схем, работающих с углом управления
Согласно (3.22) самое большое значение имеет амплитуда первой гармонической составляющей, а остальные убывают обратно пропорционально квадрату порядкового номера самой составляющей. При угле управления системы выпрямления При условии непрерывности выпрямленного тока
где
Значение переменной составляющей в выпрямленном напряжении оценивается коэффициентом пульсаций kП, который определяется как отношение амплитуды первой гармонической выпрямленного напряжения к среднему значению выпрямленного напряжения
В зависимости от числа пульсаций выпрямленного напряжения меняется значение kП. С учетом (3.22) при однофазной мостовой схеме выпрямления и активной нагрузке m =2 и kП =2/3; при трехфазной мостовой схеме выпрямления m =6 и kП =2/35. В общем случае для того, чтобы определить зависимость среднего значения выпрямленного напряжения при различном числе его пульсаций m (при любом значении m)в схемахс
на интервале одной пульсации
Например, при трехфазной неуправляемой мостовой схеме выпрямления m =6 и При использовании выпрямителей (даже если система включена на источник синусоидального напряжения) нагрузка чаще всего будет потреблять также несинусоидальный ток. Действующие значение несинусоидального периодическоготока равны
где Если учесть, что амплитуды гармонических составляющих Если нагрузка активная или активно-индуктивная, но не обеспечивается режим непрерывного тока Гармонический состав выпрямленного тока влияет на к.п.д. системы, т.к. каждая гармоника вызывает дополнительные потери и искажает форму кривой питающего напряжения.
Активная мощность выпрямленного тока равна сумме мощности постоянной составляющей (мощности постоянного тока) и активных мощностей всех его гармонических составляющих:
где Реактивной мощностью выпрямленного тока можно считать величину
Однако полная (кажущаяся) мощность несинусоидального тока
т.к. в ее выражение входят также произведения типа Мощностью искажения называется величина
т.к. она обусловлена только несинусоидальностью напряжений и токов.
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.175.197 (0.008 с.) |

 , которая является периодической, но имеет несинусоидальную форму
, которая является периодической, но имеет несинусоидальную форму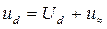
 , где Т - период функции, k – целое число (рис. 3.11). Как известно из математики, такая гармоническая функция может быть представлена в виде гармонического ряда.
, где Т - период функции, k – целое число (рис. 3.11). Как известно из математики, такая гармоническая функция может быть представлена в виде гармонического ряда. ,
, ,
, и
и  - амплитуда и начальная фаза ν-ой гармонической составляющей выпрямленного напряжения.
- амплитуда и начальная фаза ν-ой гармонической составляющей выпрямленного напряжения. .
. будет иметь значения:
будет иметь значения: ,
, - действующие значения гармонических составляющих напряжения.
- действующие значения гармонических составляющих напряжения. определяется как
определяется как (3.22)
(3.22) гармонический состав в переменной составляющей выпрямленного напряжения меняется: из рис. 3.4, 3.6, 3.7, 3.9,3.10 видно, что с ростом
гармонический состав в переменной составляющей выпрямленного напряжения меняется: из рис. 3.4, 3.6, 3.7, 3.9,3.10 видно, что с ростом  растет пульсация напряжения, а следовательно увеличивается его переменная составляющая.
растет пульсация напряжения, а следовательно увеличивается его переменная составляющая. , что соответствует наиболее распространенному режиму работы на активно-индуктивную нагрузку, амплитуды гармонических составляющих переменной составляющей выпрямленного напряжения в зависимости от угла управления
, что соответствует наиболее распространенному режиму работы на активно-индуктивную нагрузку, амплитуды гармонических составляющих переменной составляющей выпрямленного напряжения в зависимости от угла управления 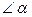 выражаются зависимостью
выражаются зависимостью , (3.23)
, (3.23) - среднее значение выпрямленного напряжения при
- среднее значение выпрямленного напряжения при  - для мостовой однофазной схемы выпрямления;
- для мостовой однофазной схемы выпрямления; - для мостовой трехфазной схемы выпрямления.
- для мостовой трехфазной схемы выпрямления. . (3.24)
. (3.24)
 и взять его среднее значение (рис. 3.12). Вследствие повторяемости напряжения ud его среднее значение на интервале T/m, будет таким же, как и на всем периоде Т. С учетом того, что период фазного напряжения
и взять его среднее значение (рис. 3.12). Вследствие повторяемости напряжения ud его среднее значение на интервале T/m, будет таким же, как и на всем периоде Т. С учетом того, что период фазного напряжения 

 (рис. 3.8).
(рис. 3.8). ,
, - действующие значения гармонических составляющих тока.
- действующие значения гармонических составляющих тока. связаны с амплитудой основной гармонической
связаны с амплитудой основной гармонической  соотношением
соотношением  ~
~  , то очевидно, что с увеличением числа фаз схемы выпрямления (с увеличением числа пульсаций m) потребляемый из сети ток приближается к синусоидальному, т.к. амплитуды высших гармонических уменьшаются.
, то очевидно, что с увеличением числа фаз схемы выпрямления (с увеличением числа пульсаций m) потребляемый из сети ток приближается к синусоидальному, т.к. амплитуды высших гармонических уменьшаются.
 - сдвиг фаз гармонических составляющих напряжения и тока.
- сдвиг фаз гармонических составляющих напряжения и тока. .
.
 .
. ,
,


