
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды степенных средних величин.Содержание книги
Поиск на нашем сайте Степенные средние, в зависимости от представления отдельных величин, могут быть простыми и взвешенными. Простая средняя рассчитывается при наличии двух и более статистических величин, расположенных в произвольном порядке. Общая формула простой средней величины имеет вид
Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы
При этом обозначено: Xi – значения отдельных статистических величин или середин группировочных интервалов; m - показатель степени, от значения которого зависят следующие виды степенных средних величин: при m = -1 средняя гармоническая; при m = 0 средняя геометрическая; при m = 1 средняя арифметическая; при m = 2 средняя квадратическая; при m = 3 средняя кубическая и так далее. Используя общие формулы простой и взвешенной средних при разных показателях степени m, получаем частные формулы каждого вида. Так, приняв m = 1, находим, что простая средняя арифметическая величина определяется по формуле
Аналогично для взвешенной средней арифметической величины получаем формулу через частоты или через доли (так как
Не представляет трудностей и вывод формул для простых и взвешенных средних квадратических и кубических величин. Несколько сложнее вывод средней гармонической при m = –1. Так, используя формулу (1.11), имеем вначале
а окончательно получим, что простая средняя гармоническая величина определяется по формуле
Аналогично выводится формула взвешенной средней гармонической величины, которая имеет следующий окончательный вид через частоты или через доли
Наиболее часто употребляются формулы средних арифметических и гармонических величин. Структурные средние величины. Структурное среднее характеризует состав статистической совокупности по одному из варьирующих признаков. К этим средним относятся мода и медиана. Мода - такое значение варьирующего признака, которое в данном ряду распределения имеет наибольшую частоту. В дискретных рядах распределений мода определяется визуально. Сначала определяется наибольшая частота, а по ней модальное значение признака. В интервальных рядах для вычисления моды используется следующая формула: Xmo - нижняя граница модальности (интервал ряда с наибольшей частотой) Mo - величина интервала fMo - частота модального интервала fMo-1 - частота интервала предшествующего модальному fMo+1 - частота интервала следующего за модальным Медианой называется такое значение варьирующего признака, которое делит ряд распределения на две равные части по объему частот. Медиана рассчитывается по разному в дискретных и интервальных рядах. 1. Если ряд распределения дискретный и состоит из четного числа членов, то медиана определяется как средняя величина из двух серединных значений рангированного ряда признаков. 2. Если в дискретном ряду распределения нечетное число уровней, то медианой будет серединное значение рангированного ряда признаков. В интервальных рядах медиана определяется по формуле: - нижняя граница медианного интервала (интервала для которого накопленная частота впервые превысит полусумму частот) Me - величина интервала - сумма частот ряда - сумма накопленных частот предшествующих медианному интервалу - частота медианного интервала Показатели вариации. Различают вариацию признака в абсолютных и относительных величинах. К абсолютным показателям относятся: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия. Все абсолютные показатели имеют ту же размерность, что и изучаемые величины. К относительным показателям относятся коэффициенты осцилляции, линейного отклонения и вариации. Показатели абсолютные. Рассчитаем абсолютные показатели, характеризующие вариацию признака. Размах вариации, представляет собой разность между максимальным и минимальным значением признака.
Показатель размаха вариации не всегда применим, так как он учитывает только крайние значения признака, которые могут сильно отличаться от всех других единиц. Более точно можно определить вариацию в ряду при помощи показателей, учитывающих отклонения всех вариантов от средней арифметической. Таких показателей в статистике два: среднее линейное и среднее квадратическое отклонение. Среднее линейное отклонение (L)представляет собой среднее арифметическое из абсолютных значений отклонений отдельных вариантов от средней.
Практическое использование среднего линейного отклонения заключается в следующем, с помощью этого показателя анализируется состав работающих, ритмичность производства, равномерность поставок материалов.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.57.173 (0.007 с.) |

 =
=  .(1.11)
.(1.11)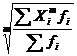 (1.12)
(1.12) =
=  . (1.13)
. (1.13) )
) . (1.14)
. (1.14) =
=  ,
, , (1.15)
, (1.15) , (1.16)
, (1.16) – для несгруппированных данных;
– для несгруппированных данных;
 – для сгруппированных данных.
– для сгруппированных данных.



