Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие индексы, необходимость их применения.Содержание книги
Поиск на нашем сайте
Общие индексы характеризуют соотношение совокупности статистических процессов или явлений, состоящей из разнородных, непосредственно несоизмеримых элементов. Для определения общей стоимости различных видов продукции в качестве со–измерителя используется обычно цена за единицу продукции, для определения общей себестоимости или производственных затрат – себестоимость единицы продукции, общих затрат труда – затраты труда на производство единицы продукции и т. д. Общее изменение товарооборота от стоимости проданных товаров можно определять, сопоставив общую стоимость проданных товаров в отчетном периоде по ценам отчетного периода с общей стоимостью проданных товаров в базисном периоде по ценам базисного периода. Формула общего индекса товарооборота:
Аналогично индексу товарооборота рассчитываются индексы продукции, потребления и т. д. Приведенная выше формула индекса товарооборота называется агрегатной (от лат. aggrega – «присоединяю»). Агрегатными называются индексы, числители и знаменатели которых представляют собой суммы, произведения или суммы произведений уровней изучаемого статистического явления. Агрегатная формула индекса – основная и наиболее распространенная формула экономических ин дексов. Агрегатная формула индекса показывает относительное изменение исследуемого экономического процесса и абсолютные размеры этого изменения. Расчет агрегатного индекса цен по данной формуле был предложен немецким экономистом Г. Пааше, поэтому его принято называть индексом Пааше. Правило построения индексов. При индексировании качественных показателей (цены, себестоимости, производительности труда) количественные берутся в отчётном периоде в числителе и знаменателе индекса, а при индексировании количественных показателей (объёма, трудозатрат) качественные берутся в базисном периоде: Такие общие индексы, как правило, называются индексами Пааше. В зарубежной статистике используются индексы Ласпейреса, где показатели фиксируются наоборот. Если нам известны некоторые данные о стоимости товара отчётного и базисного периодов, об изменении цен этих товаров в отчётном году по сравнению с базисным, изменение объёма в отчётном периоде по сравнению с базисным:
Пример. Даны следующие данные Решение:
Агрегатный индекс переходит в форму средневзвешенного, если в нем используется индивидуальный индекс. Средневзвешенный индекс, в котором индивидуальный индекс используется как делитель, носит название средневзвешенного гармонического. Средневзвешенный индекс, в котором индивидуальный индекс используется в качестве сомножителя, называется средневзвешенным арифметическим. Средние индексы. В зависимости от методологии расчета индивиду–альных и сводных индексов различают средние ариф–метические и средние гармонические индексы. Други–ми словами, общий индекс, построенный на базе индивидуального индекса, принимает форму среднего арифметического или гармонического индекса. Идея построения сводного индекса в виде средней величины из индивидуальных (групповых) индексов вполне естественна, ведь сводный индекс является об–щей мерой, характеризующей среднюю величину изме–нения индексируемого показателя, и его величина дол–жна зависеть от величин индивидуальных индексов. А критерием правильности построения сводного ин–декса в форме средней величины (среднего индекса) является его тождественность агрегатному индексу. Преобразование агрегатного индекса в сред–ний из индивидуальных (групповых) индексов произ–водится следующим образом: либо в числителе, либо в знаменателе агрегатного индекса индек–сируемый показатель заменяется его выражени–ем через соответствующий индивидуальный ин–декс. Если такую замену сделать в числителе, то агрегатный индекс будет преобразован в средний арифметический, если же в знаменателе – то в сред–ний гармонический из индивидуальных индексов. Формула свободного индекса:
Средний арифметический индекс физического объема, где весами служит стоимость отдельных ви–дов продукции в базисном периоде. В наличии имеется информация о динамике объема выпуска каждого вида продукции (iq) и стои–мости каждого вида продукции в отчетном пе–риоде (p1q1). Для определения общего измене–ния выпуска продукции предприятия в этом случае удобно воспользоваться формулой Пааше:
Числитель формулы можно получить суммирова–нием величин p1q1, а знаменатель – делением факти–ческой стоимости каждого вида продукции на соот–ветствующий индивидуальный индекс физического объема продукции, т. е. делением p1q1 / iq, тогда:
Таким образом получаем формулу среднего взвешенного гармонического индекса физического объема. Применение той или иной формулы индекса фи–зического объема (агрегатного, среднего арифмети–ческого и среднего гармонического) зависит от имею–щейся в распоряжении информации. Также нужно иметь в виду, что агрегатный индекс может быть преобразо–ван и рассчитан как средний из индивидуальных ин–дексов только при совпадении перечня видов продук–ции или товаров (их ассортимента) в отчетном и базис–ном периодах.
|
||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 284; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.115.150 (0.01 с.) |


 ;
;  ,
, 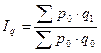 .
.
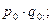
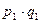 ;
; 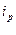 ;
; 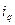 . Найти:
. Найти: 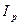 ,
, 
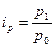 ,
, 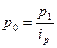 ;
; 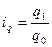 ,
,  ;
; ;
;  .
.