Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие сведения о равновесной термодинамикеСодержание книги
Поиск на нашем сайте
Первое начало термодинамики. Энтальпия. Первое начало термодинамики - один из трех основных законов термодинамики, представляющий собой закон сохранения энергии для систем, в которых существенное значение имеют тепловые процессы. Согласно первому началу термодинамики, термодинамическая система (например, пар в тепловой машине) может совершать работу только за счёт своей внутренней энергии или каких-либо внешних источников энергии. Формулировка I закона термодинамики: Невозможно построить такую машину, которая, совершая произвольное число раз один и тот же циклический процесс, приводила бы к накоплению энергии в изолированной системе. То есть вечный двигатель I рода невозможен. Первое начало термодинамики объясняет невозможность существования вечного двигателя 1-го рода, который совершал бы работу, не черпая энергию из какого-либо источника. Сущность первого начала термодинамики заключается в следующем: При сообщении термодинамической системе некоторого количества теплоты Q в общем случае происходит изменение внутренней энергии системы Δ U и система совершает работу А:
где Q – теплота, ΔU – изменение внутренней энергии, А – работа (pV, p – давление, V объем). Уравнение (1.4), выражающее первое начало термодинамики, является определением изменения внутренней энергии системы (Δ U), так как Q и А — независимо измеряемые величины. Внутреннюю энергию системы U можно, в частности, найти, измеряя работу системы в адиабатном процессе (то есть при Q = 0): А ад = — Δ U, что определяет U с точностью до некоторой аддитивной постоянной U0:
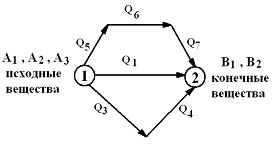
Первое начало термодинамики утверждает, что U является функцией состояния системы, то есть каждое состояние термодинамической системы характеризуется определённым значением U, независимо от того, каким путём система приведена в данное состояние (в то время как значения Q и А зависят от процесса, приведшего к изменению состояния системы). При исследовании термодинамических свойств физической системы первое начало термодинамики обычно применяется совместно со вторым началом термодинамики. Химические процессы протекают обычно либо при постоянном давлении (изобарные), либо при постоянном объёме (изохорные). В химии чаще всего приходится иметь дело с изобарными процессами. Чтобы уяснить смысл понятия энтальпия, рассмотрим следующий пример. Допустим, система переходит из одного состояния в другое: Сосуду, заполненному газом, сообщили некоторое количество тепла, и в 1 случае выдерживается постоянный объём, а во 2 – газ может свободно расширяться. В 1 случае сообщённое тепло QU полностью пойдёт на изменение внутренней энергии системы Q = ΔU (1) Во 2 случае тепло расходуется на изменение внутренней энергии ΔU и на работу А. Qp= ΔU + A (2), где А – работа по перемещению поршня Qp= ΔU + p ΔV (3), где р – давление, ΔV – изменение объёма системы. Формулу (3) можно переписать в следующем виде: Qp=(U2 – U1) + p(V2 – V1) (4) Qp=(U2 + pV2) – (U1 + pV1) (5) В этом выражении параметры в скобках обозначим Н, т.е. U2 + pV2 = Н2, U1 + pV1=Н1, тогда Qp= Н2 – Н1 =ΔН. Так, путём рассуждений мы пришли к новой термодинамической функции Н: проведён изобарный процесс, система перешла из одного состояния в другое, энергия системы увеличилась, и охарактеризовать её можно энтальпией. Энтальпия – энергия расширенной системы, или внутреннее теплосодержание системы. Для экзотермических реакций Q > 0, ΔH < 0 Для эндотермических реакций Q < 0, ΔH > 0. Количество теплоты, выделяющееся или поглощающееся при реакции, называется тепловым эффектом реакции. Изучением теплот химических реакций занимается термохимия. При исследовании тепловых эффектов разных реакций выведен ряд закономерностей. Так, например, экспериментально установлено, что тепло, выделяющееся при образовании сложного вещества из простых равно теплу, поглощаемому при разложении такого же его количества на составные части. Это явление следует рассматривать как частный случай закона сохранения энергии (з-н Лавуазье – Лапласа). Более глубокое обобщение термохимических закономерностей даёт основной закон термохимии – закон Гесса: Тепловой эффект химических реакций, протекающих при постоянном давлении или при постоянном объёме, не зависит от числа промежуточных стадий, а определяется лишь начальным и конечным состоянием системы. Например, вещество АВ можно получить из А разными способами: 1) А + В = АВ (ΔН) 2) А + С = АС (ΔН1) АС + В = АВ + С (ΔН2) ΔН1 + ΔН2 = ΔН
В термодинамике принята следующая запись теплот химических реакций: С(тв) + О2(г) = СО2(г); ∆НР = -405,8 кДж; в термохимии: С(тв) + О2(г) = СО2(г) + 405,8 кДж. ∆Н0 указывает на стандартное состояние (Р = 1 атм, Т = 298 К). Реагирующие вещества берутся в том агрегатном состоянии и в виде той кристаллической модификации, которые наиболее устойчивы при данных условиях. В термодинамике считается положительной (+) теплота, поглощенная системой (эндотермический процесс), а в термохимии – выделяемая в результате реакции (экзотермический процесс). В термохимии пользуются понятием «теплота (энтальпия) образования вещества». Под теплотой образования понимают тепловой эффект реакции образования одного моль вещества из простых веществ. Существует также понятие «стандартная теплота образования вещества» - тепловой эффект реакции образования одного моль вещества из простых веществ в стандартных условиях ( ΔН0298) (при 298 К и 1 атм) Обычно теплоты образования простых веществ в стандартных условиях принимают равными нулю. Теплоты образования приводятся в справочниках. Большое значение закона Гесса заключается в том, что, пользуясь им можно вычислить неизвестную теплоту реакции путем комбинирования стехиометрических уравнений и теплот других реакций, изученных экспериментально. При этом необходимо сравнивать теплоты различных реакций в одних и тех же условиях. Пример: Определить тепловой эффект реакции на основе экспериментальных данных при 0°С и давлении 1 атм. · С + О2 = СО2; ∆НР,1 = -405,8 кДж · СО + ½ О2 = СО2; ∆НР,2 = -284,5 кДж ______________________________________ 3) С + ½ О2 = СО; ∆НР,3 -? (3) = (1) – (2) Проверка: С + О2 - ½ О2 – СО = СО2 - СО2; С + ½ О2 = СО. ∆НР,3 = ∆НР,1 - ∆НР,2 = -405,8 кДж – (-284,5 кДж) = 121,3 кДж. Для расчетов по закону Гесса часто пользуются теплотами сгорания органических соединений, которые можно довольно легко определить экспериментально. Теплота реакции рассчитывается по I следствию закона Гесса: Теплота реакции равна сумме теплот сгорания начальных участников реакции за вычетом суммы теплот сгорания конечных участников реакции с учетом стехиометрических коэффициентов.
где νн, νк - стехиометрические коэффициенты. Пример для реакции а А + b B→ d D * ∆Hреакц. = а ∆Hсгор(А) + b ∆Hсгор(B) - d ∆Hсгор(D). • Теплотой сгорания вещества называется тепловой эффект реакции сгорания его (1 моль) с образованием устойчивых продуктов (для органических веществ это СО2 и Н2О). Кроме теплот сгорания часто используют теплоты образования химических соединений. • Теплотой образования вещества называется теплота образования Простые вещества реагируют в виде той модификации и в том агрегатном состоянии, которые наиболее устойчивы при данных условиях. Теплоты образования лишь в редких случаях могут быть определены экспериментально, чаще теплоты образования рассчитывают на основе закона Гесса. Пример: а А + b B→ d D. ∆HР = ∆Hобр(D)· d = а ∆Hсгор(А) + b ∆Hсгор(B) - d ∆Hсгор(D);
Соединения, теплоты образования которых положительны, называются эндотермическими, а теплоты образования, которых отрицательны - экзотермическими. В целях сопоставления и использования для расчетов по закону Гесса теплоты огромного количества реакций (химических соединений) рассчитаны для стандартных условий:Р = 1 атм (101300 Па); Т = 298 К (25 °С) и сведены в таблицы стандартных величин ( Пользуясь стандартными значениями можно рассчитать тепловой эффект любой реакции (при стандартных условиях) по II следствию закона Гесса: Теплота реакции равна сумме теплот образования конечных веществ за вычетом суммы теплот образования начальных веществ с учетом стехиометрических коэффициентов.
Или для стандартных условий:
Пример: а А + b B→ d D ∆HР = d ∆Hобр(D) – (а ∆Hобр(А) + b ∆Hобр(B)) = d ∆Hобр(D) - а ∆Hобр(А) - b ∆Hобр(B). При этом величина и знак теплоты образования характеризуют устойчивость соединения в данных условиях. Например:
Чем меньше ΔН, тем более устойчиво соединение. При образовании NH3 выделяется тепло. Далее в приведённом ряду теплоты образования возрастают, и, следовательно, устойчивость соединений падает. А гидрид висмута разлагается при получении. NH4Cl = NH3 + HCl↑ Из справочника выпишем энтальпии веществ:
По этим данным можно рассчитать тепловой эффект хим реакции, пользуясь 2 следствием из закона Гесса. ΔН0298(реакции) = ΔН0298(HCl) + ΔН0298(NH3) - ΔН0298(NH4Cl) = 176,55 кДж/моль Тепловой эффект положителен, т.е. реакция эндотермическая, а, значит, чтобы разложить NH4Cl, его нужно нагреть. Если известен тепловой эффект реакции, то можно рассчитать и теплоту образования вещества, участвующего в реакции. Закон Гесса позволяет также рассчитывать теплоты образования неустойчивых соединений и тепловые эффекты реакций, которые нельзя осуществить экспериментально. На практике тепловой эффект реакций измеряют с помощью калориметра. Величина ΔН зависит от агрегатного состояния вещества, поэтому в термохимических уравнениях указывают агрегатное состояние веществ. Закон Гесса является следствием первого начала термодинамики и справедлив при постоянном объёме или постоянном давлении. Второе начало термодинамики Все процессы, протекающие в природе, самопроизвольно, то есть без затраты работы извне, имеют определенное направление. Так, самопроизвольно теплота переходит от нагретого тела к холодному, газ переходит из области большего давления в область низкого, в растворах самопроизвольно выравниваются концентрации и т.д. Из I-го закона т/д нельзя сделать вывод о возможности самопроизвольного протекания процесса. Поскольку все реальные процессы протекают в определенном направлении, то для изменения направления необходимо изменить условия протекания процессов. Все реальные процессы не являются равновесными и протекают с конечной скоростью, приближая систему к равновесию. В момент наступления равновесия процесс заканчивается. Неравновесный процесс, протекающий в направлении достижения равновесия без воздействия внешних условий, называется самопроизвольным (положительным). Обратный по направлению процесс, который не может протекать без внешних воздействий и удаляющий систему от равновесия называется несамопроизвольным (отрицательным). II закон термодинамики позволяет предсказать направление протекания процесса. Он имеет несколько формулировок: · Постулат Клаузиуса Единственным результатом любой совокупности процессов не может быть переход теплоты от менее нагретого тела к более нагретому. · Постулат Томсона Теплота наиболее холодного из участвующих в процессе тел не может служить источником работы. (Теплота не может полностью перейти в работу). · Вечный двигатель второго рода невозможен, т.е. невозможно построить такую машину, которая производила бы работу за счет тепла окружающей среды, не более нагретой, чем сама машина. Т.о., процесс превращения теплоты в работу является несамопроизвольным и для его проведения необходима специальная организация такого процесса (паровая машина). Пусть Т1– температура нагревателя, Т2 – температура холодильника. Пусть имеется цилиндр с поршнем и некоторым количеством вещества, которое называется рабочим телом (например, пар). Оно совершает циклическую последовательность процессов, периодически возвращаясь в исходное состояние. КПД такой машины - отношение совершенной работы к затраченной теплоте: η = Итальянский ученый Карно рассмотрел идеальную тепловую машину, в которой рабочим телом является 1 моль идеального газа, а все процессы совершаются идеально равновесно. ηидеальн = В идеальной машине Карно совершается максимальная работа, однако КПД составляет лишь около 40%, т.к. невозможно достичь температуры холодильника 0К. В реальной тепловой машине совершается меньшее количество работы и КПД существенно ниже. Энтропия Энтропия – функция состояния термодинамической системы, используемая во втором законе т/д для выражения через нее возможности или невозможности самопроизвольного протекания процесса (введена Клаузиусом). Изменение энтропии определяется отношением количества теплоты, сообщенного системе или отведенного от нее, к температуре системы:
где знак равенства относится к равновесному процессу, неравенства – к неравновесному. Т.о. в равновесном процессе: S = По изменению энтропии в изолированной системе можно предсказать т/д возможность протекания самопроизвольного неравновесного процесса. Если энтропия увеличивается (S > 0), то самопроизвольный неравновесный процесс возможен, если S < 0 – невозможен. Т.о. все самопроизвольные процессы в изолированных системах идут в сторону увеличения энтропии до достижения равновесия, где она будет иметь постоянное и максимальное значение. В современной термодинамике второе начало термодинамики изолированных систем формулируется единым и самым общим образом как закон возрастания особой функции состояния системы, которую Клаузиус назвал энтропией (S). Физический смысл энтропии состоит в том, что в случае, когда материальная система находится в полном термодинамическом равновесии, элементарные частицы, из которых состоит эта система, находятся в неуправляемом состоянии и совершают различные случайные хаотические движения. В принципе можно определить общее число этих всевозможных состояний. Параметр, который характеризует общее число этих состояний, и есть энтропия. Рассмотрим это на простом примере. Пусть изолированная система состоит из двух тел «1» и «2», обладающих неодинаковой температурой T 1 > T 2. Тело «1» отдает некоторое количество тепла Q, а тело «2» его получает. При этом идет тепловой поток от тела «1» к телу «2». По мере уравнивания температур увеличивается суммарное количество элементарных частиц тел «1» и «2», находящихся в тепловом равновесии. По мере увеличения этого количества частиц увеличивается и энтропия. И как только наступит полное тепловое равновесие тел «1» и «2», энтропия достигнет своего максимального значения. Таким образом, в замкнутой системе энтропия S при любом реальном процессе либо возрастает, либо остаётся неизменной, т. е. изменение энтропии Δ S =0. Знак равенства в этой формуле имеет место только для обратимых процессов. В состоянии равновесия, когда энтропия замкнутой системы достигает максимума, никакие макроскопические процессы в такой системе, согласно второму началу термодинамики, невозможны. Отсюда следует, что энтропия - физическая величина, количественно характеризующая особенности молекулярного строения системы, от которых зависят энергетические преобразования в ней. Связь энтропии с молекулярным строением системы первым объяснил Л. Больцман в 1887 году. Он установил статистический смысл энтропии (формула 1.6). Согласно Больцману (высокая упорядоченность имеет относительно низкую вероятность)
где k — постоянная Больцмана, P – статистический вес. k = 1.37·10-23Дж/К. Статистический вес Р пропорционален числу возможных микроскопических состояний элементов макроскопической системы (например, различных распределений значений координат и импульсов молекул газа, отвечающих определённому значению энергии, давления и других термодинамических параметров газа), т. е. характеризует возможное несоответствие микроскопического описания макросостояния. Для изолированной системы термодинамическая вероятность W данного макросостояния пропорциональна его статистическому весу и определяется энтропией системы:
Таким образом, закон возрастания энтропии имеет статистически-вероятностный характер и выражает постоянную тенденцию системы к переходу в более вероятное состояние. Отсюда следует, что наиболее вероятным состоянием, достижимым для системы, является такое, в котором события, происходящие в системе одновременно, статистически взаимно компенсируются. В связи с этим, введена ещё одна функция – ΔG – изобарно-изотермический потенциал (Энергия Гиббса) или свободная энергия Гиббса: ΔG = ΔH – TΔS где ΔH – изменение энтальпии, Т – абсолютная температура, ΔS – изменение энтропии. Если ΔG <0, процесс протекает самопроизвольно (экзэргонический процесс), если ΔG > 0, то процесс невозможен (эндэргонический процесс). ΔG <0, если ΔH<0, т.е. реакция экзотермическая, или ΔН > 0, но по абсолютной величине меньше T · ΔS (энтропийного фактора). Значение T · ΔS резко возрастает при высокой температуре и определяет направленность процесса. Этим объясняется изменение направленности некоторых реакций с повышением температуры. Третье начало термодинамики Третье начало термодинамики - закон термодинамики, сформулированный В. Нернстом в 1906 году (тепловой закон Нернста), согласно которому энтропия S любой системы стремится к конечному для неё пределу, не зависящему от давления, плотности или фазы, при стремлении температуры (Т) к абсолютному нулю. Третье начало термодинамики позволяет находить абсолютное значение энтропии, что нельзя сделать на основе первого и второго начал термодинамики. В классической термодинамике (первого и второго начал) энтропия может быть определена лишь с точностью до произвольной аддитивной постоянной S 0, что практически не мешает большинству термодинамических исследований, так как реально измеряется разность энтропий (S 0) в различных состояниях. Согласно третьему началу термодинамики при Т = 0 значение Δ S = 0. Макс Планк в 1911 году дал другую формулировку третьего начала термодинамики - как условие обращения в нуль энтропии всех тел при стремлении температуры к абсолютному нулю:
Отсюда S 0 = 0. Это даёт возможность определять абсолютное значения энтропии и других термодинамических потенциалов. Формулировка Планка соответствует определению энтропии в статистической физике через термодинамическую вероятность (W) состояния системы S = k ln W. При абсолютном нуле температуры система находится в основном квантово-механическом состоянии, для которого W = 1 (состояние реализуется единственным микрораспределением). Следовательно, энтропия S при Т = 0 равна нулю. В действительности при всех измерениях стремление энтропии к нулю начинает проявляться значительно раньше, чем может стать существенной при T → 0 дискретность квантовых уровней макроскопической системы, приводящая к явлениям квантового вырождения. Из третьего начала термодинамики следует, что абсолютного нуля температуры нельзя достичь ни в каком конечном процессе, связанном с изменением энтропии, к нему можно лишь асимптотически приближаться.
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 274; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.49.90 (0.012 с.) |

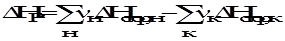
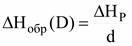
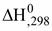 или
или  ) (стандартные теплоты образования).
) (стандартные теплоты образования).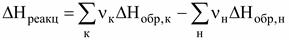
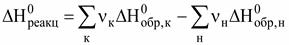

 ,
, .
.