
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория мономолекулярной адсорбции. Изотерма Ленгмюра.Содержание книги
Поиск на нашем сайте
Адсорбция бывает нелокализованная (молекулы адсорбата могут свободно перемещаться вдоль поверхности адсорбента). Локализованная адсорбция - это химическая или сильная физическая адсорбция, при которой адсорбированная молекула прочно связана с адсорбентом и не может перемещаться вдоль поверхности. Мономолекулярная локализованная адсорбция описывается уравнением изотермы адсорбции Ленгмюра:
где Г - величина адсорбции газа, Г∞ - максимально возможное количество адсорбированного вещества при образовании мономолекулярного слоя адсорбата, т. е. предельная адсорбция, в - константа адсорбционного равновесия, Р - равновесное давление газа. Уравнение (1.3), выраженное через степень заполнения Θ, имеет вид
Степень заполнения определяется по соотношению: Θ = Г/Г∞. Изотерма адсорбции Ленгмюра может быть выражена черезобъем поглощенного газа:
где V - объем адсорбированного газа, Vm - максимально возможный объем адсорбата, полностью покрывающего поверхность 1 г адсорбента. Объемы V и Vm приведены к нормальным условиям (н. у.). Площадь поверхности 1 г адсорбента Sуд - удельная поверхность:
где NA - число Авогадро, Vm выражен в литрах, 22,4 л - мольный объем газа при н. у., S0 - площадь, которую на поверхности адсорбента занимает 1 молекула адсорбата. Адсорбция из раствора описывается уравнением Ленгмюра вида
где С – равновесная концентрация адсорбированного вещества в растворе, моль/м3. Уравнение Ленгмюра можно привести к линейному виду, что позволит графически определить его константы в и Г∞.
Рис. 1. Зависимость Это уравнение прямой в координатах Sуд = Г∞NAS0. При адсорбции происходит выделение теплоты. Теплота адсорбции вычисляется по уравнению Клапейрона - Клаузиуса, так как зависимость давления, необходимого для получения одной и той же степени заполнения Θ (или величины адсорбции Г) на 1 г адсорбента, от температуры аналогична зависимости «давление пара - температура»:
Интегрирование последнего выражения в пределах от Т1 до Т2 приводит к
Уравнение изотермы адсорбции Ленгмюра на практике применимо в достаточно ограниченном диапазона величин Теория полимолекулярной адсорбции. Изотерма БЭТ. Для полимолекулярной адсорбции на твердом адсорбенте Брунауэр, Эммет и Теллер вывели уравнение изотермы адсорбции (БЭТ):
где V - общий объем адсорбированного газа, Vm - объем адсорбированного газа, соответствующий мономолекулярному покрытию всей поверхности адсорбента, Р - равновесное давление адсорбированного газа, Ps - давление насыщенного пара, с - константа при данной температуре. В соответствии с уравнением изотермы БЭТ зависимость
Рис. 2. Линейная зависимость к уравнению изотермы адсорбции БЭТ
Изотерма Фрейндлиха Для средних заполнений поверхности адсорбента используют уравнение изотермы Фрейндлиха: Г = Г = где x - количество адсорбированного вещества, моль, m - масса адсорбента в граммах, k и α- константы. Физический смысл k - это величина адсорбции при С или Р, равных 1. α характеризует степень приближения изотермы адсорбции к прямой. Обычно при адсорбции из газовой фазы α = 0,2-1,0, a из растворов — α = 0,1-0,5. Константы уравнения Фрейндлиха определяются графически после логарифмирования: lgГ=lgk+ α lgC.
Рис. 3. Зависимость lgГ = f(lgC) к уравнению Фрейндлиха
На рис. 3 показана зависимость lgГ - lgC, выражающаяся в виде прямой линии: tgφ = α. Экспериментально величина адсорбции Г из раствора на твердом адсорбенте рассчитывается по формуле:
где С0 и СР - соответственно молярная концентрация до и после адсорбции, т - масса адсорбента в г, V - объем раствора, из которого происходила адсорбция в литрах.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 355; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.16.251 (0.007 с.) |


 ,
, .
.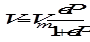
 ,
, ,
,

 = f(P) к уравнению Ленгмюра
= f(P) к уравнению Ленгмюра , actg φ = Г∞. Вместо Г и Г∞ могут быть использованы V и Vm соответственно, а вместо Р для адсорбции из раствора должна быть взята С. Величина Г∞ позволяет рассчитать удельную поверхность адсорбента по формуле:
, actg φ = Г∞. Вместо Г и Г∞ могут быть использованы V и Vm соответственно, а вместо Р для адсорбции из раствора должна быть взята С. Величина Г∞ позволяет рассчитать удельную поверхность адсорбента по формуле: .
. , откуда
, откуда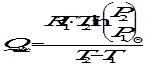 .
.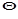 и лишь в редких случаях она выполняется во всем интервале степени заполнения поверхности от 0 до 1. Это говорит о том, что поверхность адсорбента, в основном, энергетически неоднородна.Об этом также свидетельствует зависимость теплоты адсорбции от степени заполнения, чего согласно теории Ленгмюра быть не должно. Кроме того, теория мономолекулярной адсорбции не может объяснить изотерму S – образной формы, наблюдаемую на практике, из которой следует, что адсорбция не заканчивается образованием монослояадсорбата, а продолжается дальше. Последнее явление получило объяснение с позиции полимолекулярной адсорбции. Было предложено несколько теорий полимолекулярной адсорбции, однако, наиболее приемлемой в настоящее время является теория БЭТ
и лишь в редких случаях она выполняется во всем интервале степени заполнения поверхности от 0 до 1. Это говорит о том, что поверхность адсорбента, в основном, энергетически неоднородна.Об этом также свидетельствует зависимость теплоты адсорбции от степени заполнения, чего согласно теории Ленгмюра быть не должно. Кроме того, теория мономолекулярной адсорбции не может объяснить изотерму S – образной формы, наблюдаемую на практике, из которой следует, что адсорбция не заканчивается образованием монослояадсорбата, а продолжается дальше. Последнее явление получило объяснение с позиции полимолекулярной адсорбции. Было предложено несколько теорий полимолекулярной адсорбции, однако, наиболее приемлемой в настоящее время является теория БЭТ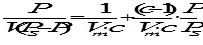 ,
, от
от  на графике дает прямую линию с тангенсом угла наклона, равным
на графике дает прямую линию с тангенсом угла наклона, равным  . На вертикальной оси отсекается отрезок, равный
. На вертикальной оси отсекается отрезок, равный  Это позволяет рассчитать значения Vm и с.
Это позволяет рассчитать значения Vm и с.
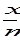 = k
= k  (адсорбция из газовой фазы);
(адсорбция из газовой фазы);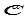 (адсорбция из раствора),
(адсорбция из раствора),
 моль/г,
моль/г,


