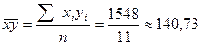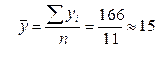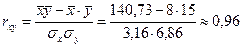Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средние величины и показатели вариацииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При анализе данных статистического наблюдения часто возникает необходимость получить обобщенную характеристику изучаемых процессов и явлений. Одной из важнейших обобщающих характеристик статистического анализа является средняя величина. В средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные действием случайных факторов, и находят выражение общие и закономерные черты, свойственные всей совокупности в целом. Средняя величина – обобщающий показатель, характеризующий типичный уровень явления в расчете на единицу однородной совокупности. В средних величинах выражается действие общих условий, закономерность изучаемого явления. Метод средних является одним из важнейших статистических методов. Основным условием правильного научного использования средней величины в статистическом анализе является качественная однородность совокупности, по которой исчислена средняя. Поэтому перед исчислением средних величин все единицы совокупности расчленяют на однородные группы, по которым и исчисляют средние. Если не произвести такого расчленения, то в результате можно прийти к результату, который совершенно неправильно будет характеризовать наблюдаемую совокупность. Метод средних неотделим от метода группировок, так как именно группировки обеспечивают качественную однородность исследуемых статистических совокупностей. Средние величины широко используются при изучении социально-правовых процессов, отражающих результаты деятельности государства, органов и учреждений, общественных структур (например, средние темпы роста и прироста объема преступности или раскрываемости, изменение структуры системы профилактики и др.). Средние величины, используемые в статистическом анализе можно разделить на два класса: степенные средние и структурные средние. Степенные средние определяются по формуле:
где х – индивидуальные значения осредняемого признака; n – число единиц совокупности z – степень средней. При подстановке в формулу различных значений z получаем выражения для вычисления различных видов степенных средних: при z = 1 – средняя арифметическая; при z = 0 – средняя геометрическая; при z = -1 – средняя гармоническая; при z = 2 – средняя квадратическая. Наиболее распространенным видом степенной средней является средняя арифметическая. Она используется в тех случаях, когда объем осредняемого признака образуется как сумма его значений у отдельных единиц рассматриваемой совокупности. В зависимости от характера исходных данных средняя арифметическая определяется двумя способами. Допустим, что количество правонарушений по 10 населенным пунктам региона за определенный период составило: 6000, 5900, 5700, 5600,5400, 5300, 4900, 4500, 3600, 3100. Требуется вычислить среднее количество правонарушений по региону. Для его определения необходимо просуммировать количество правонарушений по всем населенным пунктам и полученную сумму разделить на число населенных пунктов в регионе.
Среднее число правонарушений в регионе составило 5000. Используемая в данном примере формула называется простой средней арифметической. Простой она называется потому, что исчисляется простым суммированием индивидуальных значений признака и делением полученной суммы на объем совокупности. Эта формула применяется в тех случаях, когда исходные данные не сгруппированы (не образованы в группы по какому-то признаку) и каждой единице совокупности соответствует определенное значение признака, либо, когда все частоты (частости) равны между собой. Если же отдельные значения признака встречаются не один, а несколько, причем неодинаковое число раз, то среднюю величину рассчитывают по формуле взвешенной средней арифметической:
Для исчисления взвешенной средней выполняются следующие последовательные операции: умножения каждого варианта на соответствующую ему частоту, суммирование полученных произведений и деление полученной суммы на сумму частот. Рассмотрим пример применения взвешенной средней арифметической.
Пример 4.1. Годовая нагрузка 15 судей городского суда, специализирующихся на.рассмотрении гражданских дел различной направленности, составила: 17;42;47;47;50;50;50;63;68;68;75;78;80;80;85. Вычислить среднюю годовую нагрузку на одного судью.
Решение. В данном примере мы имеем дело с дискретным рядом, причем некоторые варианты ряда повторяются несколько раз, например, 47; 50 и т.д. Следовательно, необходимо для исчисления средней арифметической применить формулу взвешенной средней. Представим ряд в виде таблицы. Таблица 4.1
Подставим в формулу для исчисления средней арифметической взвешенной значения вариантов (количество гражданских дел) и соответствующие им частоты (количество судей).
Следовательно, средняя годовая нагрузка 15 судей городского суда составляет 60 дел.
Часто вычисление средних величин приходится производить по данным, сгруппированным в виде интервальных рядов распределения, когда значения признака представлены в виде интервалов. Для того, чтобы определить среднюю в интервальном ряду, необходимо перейти от интервального ряда к дискретному путем замены интервалов значений признака их серединами. В закрытом интервале (в котором указаны обе границы – нижняя и верхняя) серединное значение определяется как полусумма значений верхней и нижней границ. Иногда приходится иметь дело с открытыми интервалами (в которых имеется лишь одна из границ – верхняя или нижняя). В этом случае предполагается, что ширина данного интервала (расстояние между границами интервала) такая же, как и у соседнего интервала. После перехода от интервального ряда к дискретному вычисление средней производится по формуле взвешенной средней арифметической. Рассмотрим пример исчисления средней арифметической для интервального ряда. Пример 4.2. Сроки рассмотрения уголовных дел районным судом характеризуются следующим образом: до 3-х дней – 360 дел; от 3-х до 5-ти дней – 190 дел; от 5-ти до 10-ти дней – 70 дел; от 10-ти до 20-ти дней – 170 дел. Определить средний срок рассмотрения дела.
Решение. Занесем статистические данные в таблицу 4.2. Для этого представим их в виде интервального ряда. При этом первый интервал будет открытым – до 3-х дней, у него нет нижней границы. Поэтому при нахождении середины данного интервала следует принимать его величину равной величине последующего интервала: 3-5 лет. Таким образом, открытый интервал до 3-х лет будет аналогичен закрытому интервалу 1-3 года и его середина будет равна 2-м годам. Для облегчения исчисления взвешенной средней рекомендуем предварительные вычисления заносить в таблицу, в нашем случае это произведение вариантов на частоты – последний столбец. Таблица 2
Теперь воспользуемся формулой для исчисления взвешенной средней арифметической:
Как уже было отмечено выше, вторая группа средних, применяемых в статистическом анализе – структурные средние. Их используют для характеристики структуры совокупности. К структурным средним относятся такие показатели, как мода и медиана. Модой (Мо) называется значение признака (вариант), который наиболее часто встречается в исходной совокупности. В дискретном вариационном ряду Мо является вариант, имеющий наибольшую частоту. Рассмотрим порядок определения моды на примере:
Пример 4.3. При обследовании 500 уголовных дел по групповым преступлениям установлены следующие их размеры по количеству членов группы – таблица 4.3.
Таблица 4.3
Решение. Модальной величиной в данном примере будет преступная группа, состоящая из 4 человек (Мо = 4), поскольку этому значению в дискретном ряду распределения соответствует наибольшее количество уголовных дел – 250 (именно этот вариант имеет наибольшую частоту).
Для определения моды в интервальном ряду распределения сначала находят модальный интервал (интервал, которому соответствует максимальная частота), а затем моду вычисляют по формуле:
где х0 – нижняя граница модального интервала; h – ширина модального интервала; fMo – частота модального интервала; fMo-1 – частота интервала, предшествующего модальному; fMo+1 – частота интервала, следующего за модальным.
Пример 4.4.
105 уголовных дел по конкретному виду преступлений за год распределились по срокам расследования следующим образом – таблица 4.4. Найти моду. Таблица 4.4
Решение.
Наибольшей частотой в данном случае является 50 (дел), следовательно, модальный интервал будет 3-4 месяца. Воспользуемся формулой для нахождения моды в интервальном ряду и подставим необходимые значения:
Следовательно, чаще всего встречающийся срок расследования уголовных преступлений за год составил 3,5 месяца. Медиана - это значение признака, занимающее центральное место в ранжированной совокупности, при этом первая половина совокупности имеет значение признака меньше, чем медиана, а вторая имеет значения признака больше, чем медиана. Для определения медианы в дискретном вариационном ряду необходимо: 1) Вычислить накопленные частоты. 2) Определить порядковый номер медианы по формуле:
3) По накопленным частотам найти значение признака, которое имеет единица совокупности с найденным порядковым номером.
Пример 4.5. Распределение уголовных дел по срокам рассмотрения представлены в таблице 4.5. Вычислить медианное значение срока рассмотрения дел. Таблица 4.5
Решение. Сначала необходимо вычислить накопленные частоты – таблица 4.5, столбец 3. Находим такое значение накопленной частоты, которое равно или первый раз превышает значение 200:
Для того, чтобы найти медиану в интервальном ряду распределения, необходимо: 1) Вычислить накопленные частоты; 2) Определить порядковый номер медианы, используя ту же формулу, что и для дискретного вариационного ряда; 3) По накопленным частотам найти интервал, содержащий нужную нам единицу совокупности (медианный интервал); 4) Вычислить медиану по формуле:
где х0 – нижняя граница медианного интервала; h – ширина медианного интервала; fMе – частота медианного интервала;
Пример 4.6 Для иллюстрации нахождения медианы в интервальном ряду возьмем условие примера 4.4.
Решение. Сначала необходимо вычислить накопленные частоты. Воспользуемся, как и в предыдущих примерах, табличной формой записи – таблица 4.6. Таблица 4.6
Затем находим порядковый номер медианы:
Первая накопленная частота, равная или превышающая половину частот ряда (порядковый номер медианы) – это 85 (см. табл. 4.6). Следовательно, медианный интервал в данном случае «3-4 месяца». Воспользуемся формулой для нахождения медианы в интервальном ряду:
Медианное значение срока расследования составляет 3,35 месяца, т.е. первая половина уголовных дел была расследована менее, чем за 3,35 месяца, а вторая половина дел – более, чем за 3,35 месяца.
Средняя величина дает обобщающую характеристику варьирующего признака. Однако в ряде случаев этого бывает недостаточно и возникает потребность в исследовании вариации (колебаний), которые не проявляются в средней величине. Изучая результаты статистического наблюдения того или иного признака у конкретных единиц совокупности, практически всегда можно отметить различие между ними. В процессе статистического исследования того или иного количественного признака отдельные единицы наблюдения могут существенно различаться между собой даже в пределах однородной совокупности. Наблюдаемые различия индивидуальных значений признака внутри изучаемой совокупности в статистике принято называть вариацией признака. Средние величины двух или более совокупностей могут быть одинаковыми, но при этом исследуемые совокупности существенно различаются величиной вариации, т.е. в одной совокупности отдельные варианты могут далеко отстоять от средней величины, а в другой — размещаться более кучно вокруг средней. В том случае, когда значения признака имеют большое колебание, как правило, можно говорить и о большем разнообразии тех условий, которые воздействовали на исследуемую совокупность. Если отдельные варианты наблюдаемой статистической совокупности недалеко отстоят от средней величины, то можно говорить, что данная средняя величина достаточно полно отражает изучаемую совокупность, но при этом сама средняя величина ничего не говорит о возможной вариации исследуемого признака. Изучение характера и меры возможной случайной вариации распределения признаков в исследуемой совокупности является одним из ключевых разделов статистики. Вариация свойственна практически всем без исключения природным и общественным явлениям и процессам, в том числе и в юридической сфере. Для измерения величины вариации признака в совокупности используют следующие показатели размера вариации: § размах вариации, § среднее линейное отклонение, § дисперсия (средний квадрат отклонения), § среднее квадратическое отклонение, § коэффициент вариации. Размах вариации является наиболее простым измерителем вариации и представляет собой разность между максимальным и минимальным значениями признака в совокупности:
где R – размах вариации; х max – максимальное значение признака; х min – минимальное значение признака. Размах вариации учитывает лишь крайние отклонения и не отражает колеблемости всех вариант в совокупности. Для получения обобщенной характеристики распределения отклонений исчисляют среднее линейное отклонение, которое учитывает различия всех единиц совокупности. Данный показатель представляет собой среднюю арифметическую величину из отклонений индивидуальных значений признака от средней арифметической без учета знака этих отклонений.
где х i – индивидуальные значения признака;
n – объем совокупности. Данная формула представляет собой простое среднее линейное отклонение. Взвешенное среднее линейное отклонение определяется следующим образом:
где fi – частота повторений. Среднее линейное отклонение как меру вариации признака в статистическом анализе используют довольно редко, так как в большинстве случаев этот показатель не отражает степень рассеивания признака. Для преодоления недостатков среднего линейного отклонения вычисляют показатель, наиболее объективно отражающий меру вариации – дисперсию (средний квадрат отклонений). Она определяется как средняя из отклонений, возведенных в квадрат.
При возведении отклонений вариант от средней арифметической величины в квадрат положительные и отрицательные отклонения получают один и тот же положительный знак. Кроме того, большие отклонения от средней величины, будучи возведенными в квадрат, получают и больший «удельный вес», оказывая большее влияние на величину показателя вариации. Однако, возводя отклонения вариант от средней арифметической величины в квадрат, мы искусственно увеличиваем и сам показатель вариации. Чтобы преодолеть этот недостаток, вычисляется среднее квадратическое отклонение, которое исчисляется путем извлечения квадратного корня из среднего квадрата отклонения (дисперсии).
Дисперсия и среднее квадратическое отклонение являются общепринятыми мерами вариации признака. Приведенные показатели вариации выражаются именованными числами, имею те же единицы измерения, что и изучаемый признак, т.е. дают представление об абсолютной величине вариации признака. Для сравнения степени колеблемости разнородных явлений, разных по своему характеру и размерам признаков, используется относительный показатель вариации, который называется коэффициентом вариации. Коэффициент вариации дает возможность сопоставить вариацию одного и того же признака в разных статистических совокупностях, а также разнородных признаков одной и той же или различных статистических совокупностей.
где V – коэффициент вариации;
По величине коэффициента вариации судят об однородности совокупности. Если его значение не превышает 33%, то совокупность считается однородной. Рассмотрим порядок расчета показателей вариации на следующем примере.
Пример 4.7. Имеются данные промежуточной аттестации студентов одной из групп юридического факультета. 5 5 4 4 5 5 5 2 4 4 3 5 4 4 3 5 5 5 3 2 4 3 4 5 4 5 3 5 2 2 4 5 3 3 5 Найти размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Сделать выводы.
Решение. Составим таблицу для промежуточных вычислений – таблица 47. Таблица 4.7
1) Найдем средний балл по формуле взвешенной средней арифметической:
2) Размах вариации равен
3) Среднее линейное отклонение ищем по формуле взвешенного линейного отклонения
4) Дисперсия также находится в данном случае по формуле взвешенной дисперсии
5) Среднее квадратическое отклонение
6) Коэффициент вариации Вывод: коэффициент вариации меньше 33%, следовательно, данная совокупность однородная. В данном случае рассматривался пример вычисления показателей вариации для дискретного ряда. Для интервального ряда порядок вычисления показателей вариации аналогичен, а xi будет соответствовать серединам интервалов. Контрольные вопросы 1. Понятие средней величины в статистике. 2. Виды средних величин. Их краткая характеристика. 3. Средняя арифметическая. Ее виды. 4. Свойства средней арифметической. 5. Структурные средние. 6. Понятие моды и медианы. 7. Определение моды и медианы в дискретном ряду распределения. 8. Определение моды и медианы в интервальном ряду распределения. 9. Графический метод определения структурных средних. 10. Понятие вариации признака. 11. Абсолютные показатели вариации признака в совокупности. 12. Коэффициент вариации, его роль в статистическом анализе.
Задачи Задача 1. Годовая нагрузка 20 судей городского суда, специализирующихся на рассмотрении гражданских дел различной направленности, составила: 17;42;47;47;50;50;50;63;68;68;75;78;80;80;85;72;81;45;55;60. Вычислите среднюю годовую нагрузку на одного судью.
Задача 2. Возрастной состав лиц, совершивших преступления, характеризуется следующими данными: в возрасте 14-15 лет – 69,2 тыс. чел.; 16-17 лет – 138,9; 18-24 года – 363,3; 25-29 лет – 231,0; 30 лет и старше – 791,6 тыс. чел.. Вычислите средний возраст преступников.
Задача 3. Состояние преступности по населенным пунктам региона характеризуется следующими данными:
Определите моду и медиану количества совершенных преступлений. Задача 4. Имеются данные о среднем размере ущерба от преступных посягательств в результате совершения хищений чужого имущества:
Определите моду и медиану среднего размера ущерба.
Задача 5. Производительность труда следователей двух подразделений ОВД характеризуется следующими данными:
Вычислить показатели вариации производительности труда следователей в 1-ом и 2-ом подразделениях, по результатам расчета сделать выводы.
Задача 6. По данным о распределении числа правонарушений по возрасту их субъектов определить среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Сделать выводы.
Одна из основных задач, с которой встречается каждый юрист, правовед – оценка взаимосвязи между переменными, отражающими социально-правовые явления или процессы. К примеру, нередко проблему преступности молодежи рассматривают в зависимости от уровня безработицы. Неэффективность институтов социальной защиты связывают с миграционными потоками, рассматривают как последствия въезда (выезда) на территорию дополнительного числа людей и т.д. Очевидно, что точность полученных результатов будет зависеть от того, насколько полно мы учтем взаимосвязь всех возможных переменных величин при построении статистической модели изучаемого социально-правового процесса или явления. Связи в статистике классифицируют по тесноте, направлению, форме и числу факторов. По тесноте различают функциональные и статистические связи. При функциональной связи с изменением значений одной переменной вторая изменяется строго определенным образом, т.е. каждому значению факторного (независимого) признака соответствует одно, строго определенное значение результативного (зависимого) признака. В реальности функциональных связей не существует, они являются лишь абстракциями, полезными при анализе явлений. Связь, при которой каждому значению факторного признака соответствует не одно, а несколько значений результативного признака называется статистической (стохастической). По направлению связи делят на прямые ( положительные ) и обратные (отрицательные). При прямой связи направление изменения факторного признака совпадает направлению изменения результативного признака. При обратной связи направления изменения значений факторного и результативного признаков противоположны. По аналитической форме различают линейные и нелинейные связи. Линейные связи графически отображаются прямой, нелинейные – параболой, гиперболой, показательной функцией и т.п. В зависимости от количества факторов, действующих на результативный признак, существуют парные (однофакторные) и множественные (многофакторные) связи. В случае парной связи значения результативного признака обусловлены действием одного фактора, при множественной связи – нескольких факторов. Для исследования статистических связей используется целый комплекс методов: корреляционный анализ, регрессионный анализ, дискриминантный анализ, кластерный анализ, факторный анализ и др. Остановимся на рассмотрении корреляционного и регрессионного анализа. Корреляционно-регрессионный анализ как общее понятие позволяет решать следующие задачи: § измерение тесноты связи между двумя (и более) переменными величинами; § определение направления связи; § установление аналитического выражения (формы) взаимосвязи между явлениями; § определение возможных ошибок показателей тесноты связи и параметров уравнений регрессии.
Статистические методы различных обобщений, указывая на наличие прямой или обратной связи между признаками, не дают представления о мере связей, ее количественном выражении. Эту задачу решает корреляционный анализ, который позволяет установить характер взаимосвязи и количественно ее измерить. Для измерения тесноты связи между результативным и факторным признаками наиболее широко используется линейный коэффициент корреляции, который был введен К. Пирсоном. В теории разработаны различные модификации формул для расчета коэффициента корреляции.
Где
n – число наблюдений. Линейный коэффициент корреляции принимает значения в диапазоне от – 1 до 1. Чем ближе его значение по абсолютной величине к 1, тем теснее связь. Его знак указывает на направление связи: знак «–» соответствует обратной связи, знак «+» – прямой. Степень тесноты взаимосвязи признаков в зависимости от коэффициента корреляции приведена в таблице 5.1.
Таблица 5.1
Для оценки значимости коэффициента корреляции применятся t - критерий Стьюдента. Для этого определяется расчетное (фактическое) значение критерия:
Где n – объем совокупности. Расчетное значение t -критерия сравнивается с критическим (табличным), которое выбирается из таблицы значений Стьюдента (приложение 1) в зависимости от заданного уровня значимости Если Рассмотрим расчет линейного коэффициента корреляции на примере.
Пример 5.1. Из имеющихся 11 пар данных на осужденных с информацией: стаж работы/ количество изготовленных изделий, представленных в таблице 5.2, рассчитать линейный коэффициент корреляции, сделать выводы: Таблица 5.2
Решение. Допустим, что исследуемая нами зависимость между стажем работы осужденных и количеством изготовляемых ими изделий линейная, тогда для вычисления коэффициента корреляции мы можем использовать следующую формулу:
Для промежуточных расчетов составим таблицу 5.3. Таблица 5.3
Используя результаты расчетов из таблицы 5.3, вычислим линейный коэффициент корреляции. 1) 2) 3) 4)
5)
6) Подставляем полученные значения в формулу для вычисления линейного коэффициента корреляции:
Вывод. Поскольку коэффициент корреляции равен 0,96, можно говорить о том, что зависимость между стажем работы осужденных и количеством изготовляемых ими изделий сильная, прямая.
После того, как с помощью корреляционного анализа выявлено наличие статистической связи между признаками и оценена степень тесноты этой связи, переходят к математическому описанию этой зависимости, т.е. к регрессионному анализу. Регрессионный анализ позволяет установить аналитическую зависимость, в которой изменение среднего значения результативного признака обусловлено влиянием одной или нескольких независимых величин, а множество прочих факторов, также оказывающих влияние на результативный признак, принимаются за постоянные или средние уровни. Уравнение регрессии представляет собой
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 633; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.167.85 (0.012 с.) |


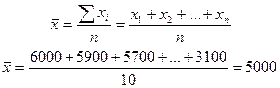


 дней
дней
 мес.
мес.
 . Этому значению соответствует накопленная частота, равная 260-ти, следовательно, медианой ряда сроков заседаний является срок продолжительностью 4 дня (Ме = 4).
. Этому значению соответствует накопленная частота, равная 260-ти, следовательно, медианой ряда сроков заседаний является срок продолжительностью 4 дня (Ме = 4).
 – накопленная частота интервала, предшествующего медианному;
– накопленная частота интервала, предшествующего медианному;
 (мес.)
(мес.)

 – среднее линейное отклонение;
– среднее линейное отклонение; – среднее значение признака;
– среднее значение признака;
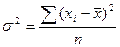 - простая дисперсия
- простая дисперсия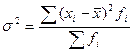 - взвешенная дисперсия
- взвешенная дисперсия

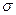 – среднее квадратическое отклонение;
– среднее квадратическое отклонение; xi -
xi - 
 балла
балла балла
балла балла
балла


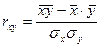

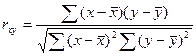
 - среднее арифметическое произведения факторного и результативного признака;
- среднее арифметическое произведения факторного и результативного признака; - среднее арифметическое результативного признака;
- среднее арифметическое результативного признака; - среднее квадратическое отклонение факторного признака;
- среднее квадратическое отклонение факторного признака;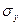 - среднее квадратическое отклонение результативного признака;
- среднее квадратическое отклонение результативного признака;
 - линейный коэффициент парной корреляции;
- линейный коэффициент парной корреляции; и числа степеней свободы k = n – 2.
и числа степеней свободы k = n – 2. , то величина коэффициента корреляции признается существенной.
, то величина коэффициента корреляции признается существенной.