
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Число обращений граждан за юридической помощью (данные условные)Содержание книги
Поиск на нашем сайте
Уровни интервального ряда в отличие от уровней моментного ряда не содержатся в предыдущих или последующих показателях. Поэтому имеется возможность суммирования этих уровней. Сумма уровней интервального ряда динамики отражает данное явление за более длительный период времени. Например, путем суммирования уровней данного ряда можно получить представление о том, сколько обращается граждан за юридической консультацией, например, за каждые последующие пять лет. По форме представления уровней различают ряды динамики абсолютных, относительных и средних величин. Ранее были приведены примеры рядов динамики абсолютных величин. Путем их обработки получают ряды относительных и средних величин, что позволяет многократно увеличить аналитические возможности временных рядов. В рядах динамики относительных величин уровни характеризуют изменение относительных размеров изучаемых явлений во времени (таблица 7.3).
Таблица 7.3 Реальные денежные доходы населения (в % к 2000г.)
В рядах динамики средних величин уровни характеризуют изменение средних размеров изучаемого явления во времени (таблица 7.4).
Таблица 7.4 Число дел, приходящееся в среднем на одного следователя в месяц (данные условные)
Основным требованием, предъявляемым к анализируемым рядам динамики является сопоставимость их уровней по кругу охватываемых объектов, по территории, по времени, по методологии расчета и другим признакам. Сопоставимость по территории означает, что данные по странам и регионам, границы которых изменились в течении анализируемого периода, должны быть пересчитаны в одних пределах. Сопоставимость по кругу охватываемых объектов подразумевает сравнение совокупностей с одинаковым числом элементов. Сопоставимость по времени обеспечивается равенством периодов времени, за которые получают данные. Сопоставимость по методологии расчета характеризуется тем, что при определении уровней ряда необходимо использовать единую методологию расчета. Для приведения рядов динамики к сопоставимому виду используют так называемое смыкание рядов (объединение двух и более временных рядов в один сопоставимый ряд). Смыкание рядов может быть произведено двумя способами: абсолютным и относительным. Остановимся на каждом из них. При абсолютном способе смыкания все уровни ряда, предшествующие переходному периоду умножаются на коэффициент перехода, равный отношению нового и прежнего уровней в переходный момент времени. В результате получаем сопоставимый ряд динамики абсолютных величин.
Пример 7.1.
Имеются данные, характеризующие количество нотариальных контор в городе N – таблица 7.5:
Таблица 7.5
Решение. Для приведения ряда динамики к сопоставимому виду для 2011 года определим коэффициент перехода:
xc – количество нотариальных контор в 2011 г. в старых границах города N, xн – количество нотариальных контор в 2011 г. в новых границах города N.
Умножая на коэффициент перехода уровни первого ряда (в старых границах города) получаем их сопоставимость с уровнями второго ряда (в новых границах):
2008 г. – 20 × 1,087 = 22; 2009 г. – 22 × 1,087 = 24; 2010 г. – 21 × 1,087 = 23.
Получим сопоставимый ряд динамики количества нотариальных контор в городе N:
Относительный способ смыкания рядов заключается в следующем: уровни ряда переходного периода принимаются за 100% и пересчитываются все остальные уровни также в % по отношению к уровням переходного периода. Результатом применения данного способа смыкания получим сопоставимый ряд динамики относительных величин.
Пример 7.2.
Для иллюстрации применения относительного способа смыкания рядов возьмем условие предыдущего примера 7.1. Для вычисления уровней нового сопоставимого ряда необходимо за 100% принять уровни переходного 2011 года. Для пересчета ряда в старых границах города мы принимаем за 100% уровень переходного периода первой части ряда, т.е. 23 – 100%. Для пересчета ряда в новых границах города мы берем за 100% уровень переходного периода первой части ряда (25 – 100%). Получаем новый сопоставимый ряд динамики относительных величин:
Для более глубокого изучения явлений и процессов, происходящих в правовой сфере и их анализа недостаточно простого сопоставления уровней временных рядов. Для характеристики изменения явлений во времени применяются специальные статистические показатели, которые называются показателями динамики. Расчет показателей рядов динамики осуществляется на основе сравнения их уровней. При этом возможны два способа сопоставления уровней временного ряда: 1) Все уровни ряда сравнивают с одним и тем же уровнем (обычно начальным), принятым за базу сравнения. В этом случае получают базисные показатели динамики. 2) Каждый последующий уровень ряда динамики сравнивают с предыдущим. Таким образом получают цепные показатели динамики. Абсолютный прирост рассчитывается как разность между сравниваемыми уровнями ряда. Он показывает на сколько единиц текущий уровень ряда больше или меньше базисного или предыдущего уровня.
цепной абсолютный прирост базисный абсолютный прирост где
Абсолютный прирост может принимать как положительные, так и отрицательные значения. Знак «+» говорит о росте уровня рассматриваемого явления за определенный период времени, знак «-» – о снижении. Темп роста – это отношение сравниваемых уровней ряда динамики, выраженное в процентах. Он показывает во сколько раз (на сколько процентов) текущий уровень больше или меньше уровня предыдущего или базисного периода.
цепной темп роста базисный темп роста
Данный показатель может принимать только положительные значения, его величина более 100% свидетельствует о росте текущего уровня по сравнению с предыдущим или базисным, менее 100% – о снижении. Темп прироста вычисляется путем вычитания из соответствующего темпа роста 100%.
цепной темп прироста базисный темп прироста
Абсолютное значение 1% прироста показывает, какое абсолютное значение содержит 1% прироста и вычисляется как отношение абсолютного прироста к темпу роста или как одна сотая от уровня предыдущего периода.
При построении и анализе временных рядов часто возникает необходимость получения обобщающих показателей динамики явлений правовой сферы, а именно: среднего уровня ряда, среднего абсолютного прироста, среднего темпа роста и среднего темпа прироста. Средний уровень ряда динамики характеризует типичную величину абсолютных уровней. В интервальных рядах динамики средний уровень определяется по формуле простой средней арифметической:
Где n – число уровней. В моментных рядах с равноотстоящими датами времени для определения среднего уровня используют формулу хронологической средней:
Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. Для определения среднего абсолютного прироста необходимо сумму цепных абсолютных приростов разделить на их число.
где Средний абсолютный прирост также можно определить по данным об уровнях ряда динамики. Для этого разность между конечным и начальным уровнями ряда делят на число субпериодов n – 1.
Средний темп роста – обобщающая характеристика индивидуальных темпов роста временного ряда. Он определяется по следующей формуле:
где Средний темп роста может быть вычислен и на основе абсолютных уровней ряда:
где
Средний темп прироста определяют на основе взаимосвязи между темпами роста и прироста:
где Проиллюстрируем порядок расчета абсолютных, относительных и средних показателей динамики на примере.
Пример 7.3.
В таблице 7.6 представлена динамика краж чужого имущества в регионе по годам (данные условные). Рассчитать абсолютные, относительные и средние показател динамики. Таблица 7.6
Решение.
Вычисленные абсолютные и относительные показатели динамики будем также заносить в таблицу 6. 1) Вычислим абсолютные цепной и базисный приросты. Абсолютный цепной прирост исчисляется по формуле:
Абсолютный базисный прирост вычислим по формуле: 2) Теперь перейдем к вычислению относительных показателей динамики. Темп роста цепной найдем по формуле Для 2011 г. его значение будет равно Для 2012 г. его значение будет равно
Аналогично получим значения
Темп роста базисный найдем по формуле
Темп прироста цепной вычисляется по формуле:
Формула для вычисления темпа прироста базисного имеет вид Абсолютное значение 1% прироста Мы рассчитали все абсолютные и относительные показатели динамики. Анализируя их, можно сказать, что в 2012 г. в регионе наблюдалось снижение количества краж чужого имущества по сравнению с 2011 г. (на 1,9%), но затем произошел их рост (в 2014 г. на 14% по сравнению с 2010 г.).
3) Теперь вычислим средние показатели динамики. Надо сказать, что предложенный для анализа ряд динамики является интервальным. Поэтому средний уровень ряда динамики будем находить по формуле
Средний абсолютный прирост будет равен:
Средний темп роста найдем по формуле
Средний темп прироста
Любой ряд динамики теоретически может быть представлен в виде составляющих: - тренд – основная тенденция развития ряда динамики; - циклические (периодические) колебания, в том числе сезонные; - случайные колебания. Важным направлением в исследовании закономерностей развития процессов правовой сферы является изучение тренда или основной тенденции развития. Основная тенденция развития – это плавное и устойчивое изменение уровней изучаемого явления во времени, свободное от случайных колебаний. Задача состоит в выделении тенденции в изменении уровней временного ряда, освобожденной от действий случайных факторов. Для решения данной задачи ряды динамики подвергаются обработке специальными методами. Наиболее распространенными методами статистического изучения тренда являются: укрупнение интервалов, сглаживание скользящей средней, аналитическое выравнивание Метод укрупнения интервалов используется для выделения тренда в ряду колеблющихся уровней, затушевывающих основную тенденцию развития. Его суть заключается в преобразовании исходного временного ряда в ряд более продолжительных периодов времени (месячных в квартальные, квартальных в годовые и т.д.). Рассмотрим пример применения метода укрупнения интервалов.
Пример 7.4. Количество мелких хищений продукции на предприятиях района характеризуется следующими данными – таблица 7.7. Выявить общую закономерность ряда динамики. Таблица 7.7
Решение. Анализируя исходный ряд динамики, можно сказать, что тенденция изменения числа мелких хищений на предприятиях района по месяцам не прослеживается. Поэтому необходимо укрупнить уровни ряда динамики до кварталов. Например, в первом квартале среднее количество хищений будет равно
Аналогично подсчитываем среднее количество хищений во 2, 3 и 4 кварталах и заносим данные в таблицу 7. В результате укрупнения уровней четко прослеживается тенденция к уменьшению числа выявленных мелких хищений на предприятиях района в течение года.
Другой метод, применяемый для статистического изучения тренда – метод скользящей средней. Он заключается в замене абсолютных уровней ряда средними арифметическими, вычисленными за определенные периоды. Вычисление средних ведется методом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением последующего. Скользящая средняя обладает достаточной гибкостью, но недостатком данного метода является укорачивание сглаженного ряда по сравнению с исходным, что ведет к потере информации. Период скольжения может быть как четным, так и нечетным. На практике удобнее использовать нечетный период, так как в данном случае скользящая средняя будет отнесена к центру периода скольжения. Например, при трехчленном периоде скольжения скользящие средние будут определяться по формулам:
Полученные скользящие средние относят к центру соответствующего периода. Особенностью сглаживания с использованием четного числа уровней заключается в том, что каждая из вычисленных скользящих средних относится к соответствующим промежуткам между смежными периодами. Для получения значений сглаженных уровней соответствующих периодов производят центрирование скользящих средних (определяется серединное значение между соседними скользящими средними). Рассмотрим применение метода скользящей средней на примере.
Пример 7.5.
Динамика аварийности на дорогах региона по месяцам представлена в таблице 7.8, столбцы 1-2 (данные условные). Выявить тренд ряда динамики при помощи метода скользящей средней.
Таблица 7.8
Решение. В данном примере мы будем использовать нечетный период скольжения, состоящий из пяти членов ряда. Первый член ряда рассчитыватся по формуле простой средней арифметической из первых пяти уровней:
Второй член ряда рассчитаем путем расчета средней из следующих пяти уровней, начиная со второго:
Далее последовательно вычисляем последующие скользящие суммы и соответствующие им средние арифметические, каждый раз сдвигаясь на один уровень ниже. Заносим полученные значения в таблицу 8, столбцы 3-4. В результате скользящая средняя пяти членов ряда, представленная в таблице 8, иллюстрирует общее направление в динамике аварийности в регионе – постепенное увеличение количества аварий.
Применение в анализе временных рядов методов укрупнения интервалов и скользящей средней позволяют выявить тренд для его описания, но получать обобщенную статистическую оценку тренда посредством данных методов не представляется возможным. Более совершенным методом изучения общей тенденции является аналитическое выравнивание. Основным содержанием этого метода является то, что основная тенденция развития явления выражается в виде функции времени:
Определение теоретических (расчетных) уровней 1. Равномерное развитие. Для этого типа динамики характерны относительно стабильные абсолютные приросты:
Основная тенденция во временных рядах со стабильными абсолютными приростами отображается уравнением линейной функции:
Где t – показатель времени. Параметр
2. Равноускоренное (равнозамедленное) развитие. Для данного типа развития характерно постоянство цепных темпов прироста:
Основная тенденция во временных рядах со стабильными темпами прироста отображается уравнением параболы второго порядка:
3. Развитие с переменным ускорением (замедлением). Для данного типа динамики основная тенденция развития отображается уравнением параболы третьего порядка:
4. Развитие по экспоненте. Для данного типа развития присуща стабильность цепных темпов роста:
Основная тенденция во временных рядах со стабильными темпами роста отображается показательной функцией:
После выяснения характера функции, по которой происходит развитие явления во времени, необходимо определить ее параметры. Чаще всего для решения этой задачи используют метод наименьших квадратов, требованием которого является минимальность отклонений суммы квадратов между теоретическими
Для нахождения параметров уравнения тренда составляется и решается система нормальных уравнений. Для равномерного развития, выражающегося в виде линейной функции эта система будет иметь вид:
Применение метода аналитического выравнивания при статистическом изучении тренда проиллюстрируем на следующем примере.
Пример 7.6.
Имеются данные о динамике совершенных преступлений несовершеннолетними в регионе за 5 лет (таблица 7.9, столбцы 1-2, данные условные). Произвести аналитическое выравнивание по прямой.
Таблица 7.9
Решение.
1) Сначала выясним, можем ли мы выравнивать данный ряд динамики по прямой. Для этого необходимо подсчитать абсолютные цепные приросты, которые, по условию выравнивания по прямой, должны быть относительны стабильны по годам. Подсчитанные 2) Для нахождения параметров уравнения тренда составляется и решается система нормальных уравнений:
где х – исходный уровень ряда динамики; n – число уровней ряда; t – показатель времени, обозначаемый порядковыми номерами, начиная от низшего (табл. 9, столбец 4). Произведем промежуточные вычисления коэффициентов системы нормальных уравнений (таблица 9, столбцы 5-6). Подставим их в систему нормальных уравнений:
Решив данную систему, получим значения параметров уравнения прямой: а0 = 18,4 и а1 = 1,34.
Итак, мы получили следующее уравнение прямой: Подставляя значения ti из таблицы9 в эту формулу, получаем теоретически выравненные значения Параметр а1 = 1,34 показывает, что количество совершенных преступлений несовершеннолетними в регионе росло в среднем на 1,34 тыс. в год.
При изучении многих социально-правовых явлений и процессов нередко обнаруживаются определенные повторяющиеся колебания, которым присущи относительно устойчивые изменения уровней временного ряда на протяжении рассматриваемого периода. Такие колебания называют сезонными. Такие колебания являются результатом влияния социальных и естественно-климатических причин, общих экономических факторов, а также других факторов, которые чаще всего являются регулируемыми. В рамках изучения преступности такие колебания хорошо просматриваются при совершении краж, в зимний период возрастает число краж из дачных домиков, а в летний период увеличивается число краж из квартир, на железнодорожном транспорте и т.д. Практическое значение статистического изучения сезонных колебаний состоит в том, что получаемые при анализе рядов внутригодовой динамики количественные характеристики отображают специфику развития изучаемых процессов по месяцам и кварталам годового цикла. Для измерения сезонных колебаний вычисляют индексы сезонности Для рядов внутригодовой динамики, в которых повышающийся (снижающийся) тренд незначителен или отсутствует, индексы сезонности рассчитывают способом постоянной средней:
где
Поскольку на сезонные колебания могут накладываться случайные отклонения, для их устранения производится усреднение индивидуальных индексов одноименных внутригодовых периодов анализируемого ряда динамики. Поэтому для каждого периода годового цикла определяются средние индексы сезонности:
Рассмотрим порядок вычисления индексов сезонности на следующем примере.
Пример 7.7.
На основе данных о квартирных кражах в городе N по кварталам за 2 года (таблица 7.10, данные условные) вычислить индексы сезонности.
Таблица 7.10
Решение. Искомые индексы сезонности будем рассчитывать способом постоянной средней:
где
Для этого сначала вычислим средние значения числа квартирных краж для каждого года.
где х 2013-1, …., х 2014-4 – число квартирных краж по кварталам каждого года.
Теперь рассчитаем индексы сезонности и занесем их значения в таблицу.
Индексы сезонности для остальных периодов рассчитываются аналогично (см. таблица 10). Средние индексы сезонности вычислим по формуле:
Так, для первого квартала средний индекс сезонности будет равен:
Значения средних индексов сезонности для трех других кварталов определяются аналогично. Занесем их также в таблицу 10. Данные таблицы 10 позволяют сделать вывод о том, что совершение квартирных краж имеет выраженную сезонность. Очевидно, что их количество возрастает с наступлением периода отпусков – в 3-м квартале. Это наглядно подтверждается кривой сезонной волны, представленной на рисунке 7.1.
Рисунок 7.1. – График сезонной волны
Определяемые при анализе временных рядов показатели изменения уровней, тренда, сезонных колебаний имеют широкое применение при прогнозировании, т.е. при получении статистической оценки возможного уровня развития социально-правовых явлений в будущем. Основой большинства методов прогнозирования является экстраполяция, т.е. распространение выявленных в анализе рядов динамики закономерностей изучаемого явления на будущее. В основе прогнозирования лежит предположение, что закономерность, действующая внутри рассматриваемого ременного ряда, сохраняется и в дальнейшем. Важное значение при экстраполяции имеет продолжительность базисного ряда динамики и сроков прогнозирования. Практика прогнозирования динамики социально-правовых явлений показывает, что при экстраполяции следует использовать те периоды базисного временного ряда, которые составляют определенный этап в развитии изучаемого процесса. Установление сроков прогноза зависит от задач исследования, однако, надо иметь в виду, что, чем короче срок прогноза, тем более надежными являются результаты экстраполяции. При прогнозировании могут использоваться различные методы экстраполяции в зависимости от исходной информации. Упрощенные приемы прогнозирования основаны на применении средних показателей динамики и используются при недостаточной информации о предыстории развития явления. Среди них можно выделить следующие методы: 1. Метод среднего абсолютного прироста. Данный метод используется для экстраполяции уровней развития изучаемого явления на базе ряда динамики с постоянными абсолютными приростами (
где
t – срок прогноза.
Пример 7.8. Для иллюстрации применения м
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.253.84 (0.01 с.) |

 , где
, где

 - уровень текущего периода;
- уровень текущего периода; - уровень предыдущего периода;
- уровень предыдущего периода;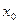 - начальный уровень ряда.
- начальный уровень ряда.


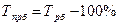

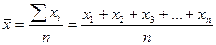
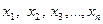 - уровни ряда динамики;
- уровни ряда динамики;

 - цепные абсолютные приросты ряда динамики.
- цепные абсолютные приросты ряда динамики.

 - индивидуальные цепные темпы роста (выраженные в коэффициентах).
- индивидуальные цепные темпы роста (выраженные в коэффициентах).
 - конечный уровень ряда;
- конечный уровень ряда;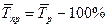
 - средний темп роста.
- средний темп роста. , тыс.
, тыс.
 , тыс.
, тыс.
 , %
, %
 , %
, %
 , %
, %
 , %
, %
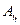
 тыс. Аналогично вычисляется абсолютный цепной прирост для последующих лет (см. табл. 6).
тыс. Аналогично вычисляется абсолютный цепной прирост для последующих лет (см. табл. 6). тыс. Занесем вычисленные значения
тыс. Занесем вычисленные значения  .
. .
. . Аналогично получим значения
. Аналогично получим значения  . По аналогии рассчитаем темпы прироста цепные для других периодов – табл. 6.
. По аналогии рассчитаем темпы прироста цепные для других периодов – табл. 6. . Занесем вычисленные значения
. Занесем вычисленные значения  . Рассчитаем
. Рассчитаем  тыс. краж.
тыс. краж. тыс. краж.
тыс. краж. . В данной формуле необходимо использовать темпы роста, выраженные не в процентах, а в коэффициентах.
. В данной формуле необходимо использовать темпы роста, выраженные не в процентах, а в коэффициентах. 



 и т.д.
и т.д.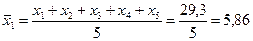


 осуществляют на основе математической функции, которая наилучшим образом отображает развитие изучаемого процесса во времени. Одним из условий применения метода аналитического выравнивания является знание типов развития социально-правовых явлений во времени и их отличительных признаков. Наиболее часто используют следующие типы развития процессов:
осуществляют на основе математической функции, которая наилучшим образом отображает развитие изучаемого процесса во времени. Одним из условий применения метода аналитического выравнивания является знание типов развития социально-правовых явлений во времени и их отличительных признаков. Наиболее часто используют следующие типы развития процессов:

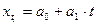
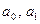 – параметры уравнения тренда;
– параметры уравнения тренда; называется коэффициентом тренда, он определяет направление развития явления. Если
называется коэффициентом тренда, он определяет направление развития явления. Если 




 уровнями ряда динамики:
уровнями ряда динамики:




 . В нашем случае эти суммы совпадают и равны 112,1. Следовательно, выравнивание по прямой было произведено верно.
. В нашем случае эти суммы совпадают и равны 112,1. Следовательно, выравнивание по прямой было произведено верно. . В общем виде они определяются отношением эмпирических (исходных) уровней ряда динамики к теоретическим (расчетным) уровням, выступающим в качестве базы сравнения. В результате того, что измерение сезонных колебаний производится на базе соответствующих теоретических уровней тренда, в исчисляемых при этом индексах сезонности влияние основной тенденции развития устраняется (элиминируется).
. В общем виде они определяются отношением эмпирических (исходных) уровней ряда динамики к теоретическим (расчетным) уровням, выступающим в качестве базы сравнения. В результате того, что измерение сезонных колебаний производится на базе соответствующих теоретических уровней тренда, в исчисляемых при этом индексах сезонности влияние основной тенденции развития устраняется (элиминируется).
 - средний уровень ряда.
- средний уровень ряда.
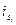






 ). При этом прогнозируемый уровень вычисляется по формуле:
). При этом прогнозируемый уровень вычисляется по формуле: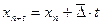
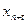 – экстраполируемый уровень;
– экстраполируемый уровень; – средний абсолютный прирост;
– средний абсолютный прирост;


