
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средние величины как статистические показателиСодержание книги
Поиск на нашем сайте
Средние величины как статистические показатели Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности. Виды средних величин и методы их расчета 1.степенные средние; 2.структурные средние. Различные средние выводятся из общей формулы степенной средней:
Средние величины бывают простые и взвешенные. Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи с чем каждый вариант приходится умножать на эту численность. Средняя арифметическая - самый распространенный вид средней. Формула средней арифметической (простой) имеет вид
где n - численность совокупности. При расчете средних величин отдельные значения признака, который осредняется, могут повторяться, поэтому расчет средней величины производится по сгруппированным данным. В этом случае речь идет об использовании средней арифметической взвешенной, которая имеет вид
Средняя гармоническая. Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1. Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1:
В статистической практике чаще используется гармоническая взвешенная, формула которой имеет вид
Средняя геометрическая. Для простой средней геометрической
Для взвешенной средней геометрической
Средняя квадратическая величина. Основной сферой ее применения является измерение вариации признака в совокупности (расчет среднего квадратического отклонения). Формула простой средней квадратической
Формула взвешенной средней квадратической
Структурные: Мода-то значение, которое встречается чаще всего Хмо=МО
Медиана-значение,к-тое находится в центре ранжированного ряда.
Изучение взаимосвязи соц.-эк. явлений. Связь наиболее общий вид: -Стохантическая связь, когда в результате изменения одного явления меняется закон; -Корреляционная связь, когда одному значению 1-ого явления соответствуют множество значения 2 явления; -Функциональная связь, когда за изменением одного явления следует строгое определенное изменения второго. Виды:1.По направлении.: -прямые; -обратные. 2.По аналитическому выражению:-линейные; -нелинейные. 3.По коли-ву влияющих признаков:-однофакторные; -многофакторные. Методы:1)Аналитическая группировка: 2)сравнение параллельных рядов; 30графический(диаграмма рассеивания);4)корреляционный анализ; 5)дисперсионный анализ; 6)регрессионный анализ.. Ряды динамики и их применение в анализе Ряды динамики - это значения статистических показателей, которые представлены в определенной хронологической последовательности. Каждый динамический ряд содержит две составляющие: 1) показатели периодов времени; 2) показатели, характеризующие исследуемый объект за временные периоды или на соответствующие даты, которые называют -уровнями ряда. Различают ряды динамики: 1) интервальный ряд содержит значения показателей за определенные периоды времени. 2) моментный ряд отражает значения показателей на определенный момент времени (дату времени). 3)ряды с нарастающими итогами (кумуметивные). 4)производные ряды: -из ср.значений; -из относительных значений. Учет основных фондов. 1)О.Состав основных фондов – совокупность произведённых активов, кот. многократно, не менее года, участвуют в создании материально-производственных ценностей. 2)О.Амортизация – потребление основных фондов в денежном выражении. Она представляет собой процесс переноса стоимости основных фондов на издержки пр-ва.
Годовая норма амортизации в %:
3)Способы вычисления амортизации: -линейный (сумма начисляется равными долями по установленной годовой норме); -пропорционально объёму произведённой продукции; -по сумме срока полезного использования. 4)Ежегодно строятся балансы основных фондов: -по полной первоначальной стоимости:
-по остаточной стоимости:
5)Показатели основных фондов: Показатели состояния основных фондов (рассчитываются на начало и конец года): -коэф. износа:
-коэф. годности: Статистика цен и тарифов. 1)О.Цена – денежное выражение произведенной продукции или услуг, которое отображает общественно необходимые затраты труда, связанные с их производством, и обращено к конечному потреблению. 2)О.Тариф - это распространенная форма (ставка оплаты) определения цены на продукцию (услуги) производственного и личного потребления. 3)Классификация цен и тарифов: По сферам товарного обслуживания: -оптовые; -розничные; -закупочные цены; -цены и тарифы на услуги транспорта. По формам продажи: -договорные; -биржевые; -аукционные. По стадиям продажи: -цена предложения (цена продавца); -цена спроса; -цена реализации. По степени регулирования: -фиксированные; -регулируемые; -свободные. По степени стойкости во времени: -твердые; -подвижные; -скользящие; -сравниваемые. 4)В условиях рыночной экономики в стране возможна инфляция – процесс непроизвольного повышения общего уровня цен и обесценивания денег, что вызвано разбалансированностью между денежной -децельный коэф. дифференциации доходов:
-коэф. фондов:
-индекс концентрации доходов Джимми (исп. для измерения фактич. располог. доходов по группам населения от их равномерного распределения):
Используется совместно с кривой Ласпереса:
Чем больше отклонение кривой от прямой, тем выше дифференциация доходов в обществе. -коэф. бедности (отношение числа граждан чьи доходы ниже прожит. минимума к общей числ. нас.). Экологическая статистика. Экологическая статистика хар. Состояние почвы, воздуха и т.д. Показатели:1. Площадь земли различного назначения, сельско.хоз. угодий. 2.обеспеченность землей населения. 3. содержание в воздухе вредных веществ и сравнение с ПДК. 4. ежедневная потребность воды на 1 жителя. 5. объем сброса пром.отходов в водоемы, степень загрязнения водоемов. 6.Коефичиент лесистости. Общая площадь. 7. объем вырубки и лесовостановления.
Статистика здравоохранения. Показатели: 1.Показатели здоровья населения: 1)доля мертворожденных 2)коэф.детской смертности 3)детей с отклонениями 4)число абортов 5)число инвалидов, их структура по группам и причинам инвалидности. 6)заболеваемость в продецелях по основным классам болезний: -сердечные -злокачественные опухли -травмы и отравления -органы дыхания, пищеварения -инфаркт 7)наркологические и псих. расстройства. В отношении всех болезней статистика учитывает кол-во людей с первые установленными заболеваниями и общее кол-во заболеваний. 2. Показатели дея-ти учреждений здравоохранения: 1)материально техническая база организации 2)обеспеченность учреждения кадров в продецелях и на 10тыс. населения 3)численность выпускников мед.учреждений 3. Показатели дея-ти мед. учреждений: 1) число лиц, к-рые оказана помощь 2)кол-во койко дней. 3)коэф. смертности и выздоровления 4. Показатели финансирования здравоохранения.
34.Статистика образования, науки и культуры. Показатели: 1) численность учеб. заведений 2)Структура профессорского преподавательского состава 3)численность обучающихся 4)коэф. обеспеченности детей детскими садами к общему числу детей до 7 лет 5) научно технические работы 6)кол-во научных исследователей 7)численность культурно-просветительных учреждений: -в целом; -в среднем 8) дея-ть СМИ 9) наличие и исп. свободного времени.
1. Статистика как наука и отрасль практической деятельности. 2. Программа статистического наблюдения. 3. Ошибки статистического наблюдения. 4. Сводка и группировка данных. 5. Табличное представление данных в статистике. 6. Графическое представление данных в статистике. 7. Абсолютные и относительные статистические показатели. 8. Средние показатели. 9. Изучение взаимосвязи социально-экономических явлений: понятие связи, виды связей. 10. Индексный метод в статистике. 11. Ряды динамики: понятие, состав, виды. 12. Методы выявления тенденции рядов динамики. 13. Статистика населения: понятие, задачи, движение населения. 14. Показатели естественного движения населения. 15. Миграция, показатели миграции населения. 16. Статистика рынка труда: экономически активное население, показатели занятости и безработицы. 17. Статистический учет рабочей силы на предприятии. 18. Рабочее время, фонды рабочего времени. 19. Статистика производительности труда: понятие, виды, уровни. 20. Статистика оплаты труда и затрат на рабочую силу: фонды заработной платы, уровни заработной платы. 21. Система национальных счетов: понятие, виды счетов. 22. Макроэкономические показатели. 23. ВВП и методы его расчета. Перерасчет ВВП в постоянных ценах. 24. Статистика национального богатства: классификация экономических активов. 25. Основные и оборотные фонды: понятие, состав, учет. 26. Статистический учет продукции предприятия 27. Статистический учет продукции торговли и общественного питания. 28. Статистика издержек производства и обращения. 29. Статистика цен и тарифов: виды цен, индекс цен. 30. Статистика уровня жизни населения: понятие уровня жизни, обобщающие показатели уровня жизни. 31. Показатели доходов населения. 32. Экологическая статистика 33. Статистика здравоохранения. 34. Статистика образования, науки и культуры.
Средние величины как статистические показатели Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности. Виды средних величин и методы их расчета 1.степенные средние; 2.структурные средние. Различные средние выводятся из общей формулы степенной средней:
Средние величины бывают простые и взвешенные. Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи с чем каждый вариант приходится умножать на эту численность. Средняя арифметическая - самый распространенный вид средней. Формула средней арифметической (простой) имеет вид
где n - численность совокупности. При расчете средних величин отдельные значения признака, который осредняется, могут повторяться, поэтому расчет средней величины производится по сгруппированным данным. В этом случае речь идет об использовании средней арифметической взвешенной, которая имеет вид
Средняя гармоническая. Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1. Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1:
В статистической практике чаще используется гармоническая взвешенная, формула которой имеет вид
Средняя геометрическая. Для простой средней геометрической
Для взвешенной средней геометрической
Средняя квадратическая величина. Основной сферой ее применения является измерение вариации признака в совокупности (расчет среднего квадратического отклонения). Формула простой средней квадратической
Формула взвешенной средней квадратической
Структурные: Мода-то значение, которое встречается чаще всего Хмо=МО
Медиана-значение,к-тое находится в центре ранжированного ряда.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 406; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.01 с.) |

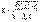
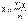

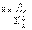
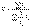

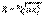
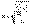

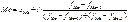
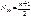

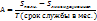
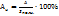 , (2-10% в год)
, (2-10% в год)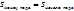 + введённые в действие + прочие поступления – выбывшие по износу – прочие выбытие
+ введённые в действие + прочие поступления – выбывшие по износу – прочие выбытие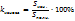



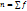 /
/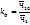
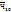 – ср. знач. суммарных доходов у 10% самой богатой части населения.
– ср. знач. суммарных доходов у 10% самой богатой части населения.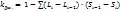 /
/



