
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютные показатели вариацииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
К абсолютным показателям вариации относятся следующие показатели: · размах колебаний; · среднее линейное отклонение; · среднее квадратическое отклонение; · дисперсия; · квартильное отклонение; 5.1.1. Размах колебаний (размах вариации): R = Хmax – Хmin, где: Хmax, Хmin – соответственно максимальное и минимальное значение признака.
5.1.2. Среднее линейное отклонение ( а) для несгруппированных данных (первичного ряда):
б) для вариационного ряда:
5.1.3. Дисперсия (
а) для несгруппированных данных:
б) для вариационного ряда:
Формула для расчета дисперсии может быть преобразована:
т.е. дисперсия равна средней из квадратов индивидуальных значений признака минус квадрат средней величины. Следовательно:
5.1.4. Среднее квадратическое отклонение (
а) для несгруппированных данных:
б) для вариационного ряда:
Среднее квадратическое отклонение по своей величине всегда превышает значение среднего линейного отклонения в соответствии со свойством мажорантности средних.
5.1.5. Квартильное отклонение (dк) применяется вместо размаха вариации, чтобы избежать недостатков, связанных с использованием крайних значений: dк = Q
Относительные показатели вариации Для оценки интенсивности вариации и сравнения ее в разных совокупностях, а также сравнения различных признаков совокупности применяются относительные показатели вариации. Они вычисляются как отношения абсолютных показателей силы вариации к средней арифметической величине (или медиане) признака и чаще всего выражаются в процентах. Существуют следующие относительные показатели: · относительный размах вариации или коэффициент осцилляции · относительное линейное отклонение или коэффициент линейного отклонения · коэффициент вариации · относительный показатель квартильной вариации · относительный показатель децильной вариации
5.2.1. Относительный размах вариации или коэффициент осцилляции:
Отражает относительную меру колеблемости крайних значений признака вокруг средней величины.
5.2.2. Относительное линейное отклонение или коэффициент линейного отклонения:
Отражает долю усредненного значения абсолютных отклонений от средней величины.
5.2.3. Коэффициент вариации:
Отражает долю относительного квадратического отклонения от средней величины. Коэффициент вариации – наиболее часто применяемый относительный показатель вариации. Его используют не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации (V) не превышает 33% (для распределений, близких к нормальному):
V < 33%
5.2.4. Относительный показатель квартильной вариации:
5.2.5. Относительный показатель децильной дифференциации (вариации):
Он показывает, во сколько раз наименьший уровень признака из 10% единиц, имеющих наибольший уровень признака, больше наибольшего уровня признака, из 10% единиц совокупности, имеющих наименьший уровень признака. Относительные показатели квартильной и децильной вариации также служат для характеристики однородности совокупности.
Моменты в рядах распределения
Исчисление дисперсий (σ2) сопровождено громоздкими расчетами, так как средняя величина (
Моментом распределения (Мк) называется средняя арифметическая из отклонения значений признака Хi от некоторой постоянной величины a в степени k. Порядок момента определяется величиной степени k.
Моменты бывают условные, начальные и центральные. Эмпирический момент k - го порядка определяется по формуле:
Мк = В зависимости от постоянной а различают начальные и центральные моменты.
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 2782; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.119.247 (0.01 с.) |

 ) определяется по формулам:
) определяется по формулам:

 ):
):

 ,
,
 ):
):


 , где:
, где: и Q
и Q 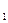 - соответственно первая и третья квартили распределения.
- соответственно первая и третья квартили распределения.


 или
или 
 * 100%
* 100% ) часто бывает выражена числом с несколькими десятичными знаками. Расчеты можно упростить, используя математические свойства дисперсии, например, расчет дисперсии по способу отсчета от условного нуля, или способу моментов.
) часто бывает выражена числом с несколькими десятичными знаками. Расчеты можно упростить, используя математические свойства дисперсии, например, расчет дисперсии по способу отсчета от условного нуля, или способу моментов. (условный момент)
(условный момент)


