
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация статистических показателей по различным признакамСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Статистический показатель – обобщающая характеристика явления или процесса, которая характеризует всю совокупность единиц и используется для анализа совокупности в целом.
Количественная сторона статистических показателей характеризует размеры явлений, уровень явлений и соотношение показателей в явлении.
Качественная сторона показателей показывает содержание явления или процесса.
Система статистических показателей – это совокупность взаимосвязанных показателей, имеющих одноуровневую или многоуровневую структуру, и нацеленную на решение конкретных задач.
В отличие от признака, статистический показатель получается расчетным путем, начиная от элементарной суммы единиц и заканчивая сложными расчетами.
Различают конкретный статистический показатель и показатель-категорию. Конкретный статистический показатель характеризует размер, величину изучаемого явления или процесса в данном месте и в данное время. Показатель-категория отражает сущность, общие отличительные свойства конкретных статистических показателей одного и того же вида без указания места, времени и числового значения.
Показатели разделяются на виды в зависимости: 1. Способа их вычисления. 2. Признаков времени. 3. Выполнение тех или иных функций.
По способу вычисления различают первичные показатели и производные показатели. Первичные – с помощью сводки и группировки суммирование единиц совокупности. Производные – вычисляются на базе первичных и имеют форму средних или относительных величин.
Обратные показатели – показатели, которые существуют параллельно и характеризуют один и тот же процесс.
Индивидуальные – характеризуют единицу совокупности. Сводные показатели – характеризую совокупность единиц. Делятся на: Объемные показатели – получаются путем суммирования (объем совокупности). Расчетные показатели – вычисляются по формулам и служат для вычисления взаимосвязи, взаимозависимости (индексы, ошибка выборки).
По признаку времени показатели разделяются на интервальные и моментные. Интервальные характеризуют за определенный период. Моментные характеризуют за данный момент времени.
По способу выполнения своих функций – показывают изменения во времени о пространстве.
В статистике используют несколько разновидностей статистических показателей: — абсолютные и относительные величины; — средние величины; — показатели вариации.
Абсолютные величины — это именованные числа и в зависимости от характера явления или процесса могут иметь разные единицы измерения: · натуральные (кг, м, шт. и унции, квадратные, кубические и простые метры, мили, километры, галлоны, литры и т.д.); · условно-натуральные (консервы различного объема в одну условную банку консервов, одна условная единица минеральных удобрений и т. д.).
Перевод в условные единицы измерения осуществляется на основе специальных коэффициентов, рассчитываемых как отношение потребительских свойств отдельных разновидностей продукта к их эталонному значению.
В отдельных случаях для характеристики какого-либо явления или процесса одной единицы измерения недостаточно и используется произведение двух единиц. Например, показатели грузооборота и пассажирооборота, оцениваемые соответственно в тонно-километрах и пассажиро-километрах, производство электроэнергии, измеряемое в киловатт-часах, · трудовые (человеко-час, человеко-день); · стоимостные (руб., дол. США, евро и др.).
На основании этих абсолютных показателей рассчитываются обобщающие показатели.
Относительные величины — это обобщающие количественные показатели, которые выражают соотношение сравниваемых абсолютных величин. Поэтому по отношению к абсолютным показателям относительные показатели или показатели в форме относительных величин являются производными (вторичными). Логической формулой относительной величины является такая обычная дробь:
Величина сравнения Относительная величина = ---------------------------------- База сравнения
Относительные показатели могут выражаться в коэффициентах (1), процентах (100), промилле (1000), продецимилле (10000) или быть именованными числами (если берутся разноименные абсолютные показатели).
Все используемые на практике относительные статистические показатели можно подразделить на следующие виды: • динамики; • плана; • реализации плана; • структуры; • координации; • интенсивности и уровня экономического развития; • сравнения.
Относительный показатель динамики (ОПД) представляет собой отношение уровня исследуемого процесса или явления за данный период времени (по состоянию на данный момент времени) к уровню этого же процесса или явления в прошлом:
Различают относительные показатели динамики с постоянной (базисные показатели) и переменной базой сравнения (цепные показатели).
Произведение всех относительных показателей с переменной базой будет равно относительному показателю с постоянной базой за исследуемых период.
Относительные показатели плана (ОПП) и реализации плана (ОПРП):
Между относительными показателями плана, реализации плана и динамики существует следующая взаимосвязь: ОПП*ОПРП=ОПД.
Относительный показатель структуры (ОПС) характеризуют состав, структуру совокупности по тому или иному признаку и показывают вклад составляющих совокупности в общую массу. Они определяются отношением размеров составных частей совокупности к общему итогу.
Относительные показатели координации (ОПК) характеризуют соотношение отдельных частей целого между собой, и показывают, сколько единиц одной части совокупности приходится на 1, 100, 1000 и больше единиц другой, взятой за базу сравнения.
Относительный показатель интенсивности (ОПИ) характеризует степень распространения изучаемого процесса или явления в присущей ему среде.
Относительные показатели сравнения (ОПСр) в обычном понимании характеризуют сравнение одноименных показателей, принадлежащих к разным объектам, взятых за тот же период или момент времени. Вычисляется в относительных величинах или процентах.
Относительные величины сравнения также включают относительные величины пространственного сравнения и относительные величины сравнения со стандартом.
Относительная величина дифференциации – вычисляется в результате сравнения двух структурных рядов, один из которых характеризует соотношение частей совокупности по численности единиц, а второй – по величине любого признака (например, сравнение удельного веса хозяйств по численности и удельного веса в этих хозяйствах валовой продукции, основных фондов, работников и т.п.)
Средние величины
Средняя величина признака – обобщающий показатель, характеризующий типический уровень явления.
Сущность средней заключается в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных.
Типичность средней непосредственным образом связана с однородностью статистической совокупности.
Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности (средняя зарплата по стране - статистическая).
Правила применения средних величин: — необходимо исходить из качественного содержания признака; — средняя величина должна рассчитываться по однородной совокупности; — необходим обоснованный выбор единицы совокупности.
При использовании средних величин введем такие обозначения: x̅ - среднее значение исследуемого признака хi или x - каждое индивидуальное значение (варианта в вариационном ряду) fi или f - частота повторений (вес) индивидуального признака w - объем значений признака n - количество единиц исследуемого признака
Средние величины подразделяются на степенные и структурные. Формулы расчета степенных средних можно записать в общем виде:
- простая формула - - взвешенная формула
при k=1 “средняя арифметическая”
при k=2 “средняя квадратическая”
при k=3 “средняя кубическая”
при k=-1 “средняя гармоническая”
“средняя геометрическая” (k=0)
С увеличение степени k значение степенной средней увеличивается, т.е. для одной и той же совокупности справедливо
x̅-1 ≤ x̅0 ≤ x̅1 ≤ x̅2 ≤ x̅3 ≤ …
т.е. при увеличении степени средняя величина увеличивается (правило мажоритарности средних). Пользуясь правилом статистика может в зависимости от настроения и желания ее «знатока» может как «утопить», так и «выручить».
Средняя арифметическая взвешенная При расчете величин отдельные значения осредняемого признака могут повторяться, встречаться по нескольку раз. В подобных случаях расчет средней производится сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными.
Использовать среднюю арифметическую невзвешенную только тогда, когда точно установлено отсутствие весов или их равенство.
При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их серединам.
Способ моментов Если интервальный ряд имеет равные интервалы или дискретный ряд построен с одни и тем же шагом между ближайшими значениями признака, для расчета средней применим способ моментов.
Алгоритм: 1. строится новый дискретный ряд распределения, в котором один из вариантов приравнивается к нулю. 2. остальные варианты нового ряда обозначаются и рассчитываются по формуле: x`=(x-x0)/h h – ширина равного интервала или шага x` - условные варианты 3. определяется средняя по способу моментов.
Свойства средней арифметической Средняя арифметическая обладает некоторыми математическими свойствами, более полно раскрывающими ее сущность и в ряде случаев используемыми при ее расчетах. Рассмотрим эти свойства 1. произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты 2. сумма отклонений индивидуальных значений признака от средней арифметической равна нулю 3. если все осредняемые варианты увеличить или уменьшить на постоянное число А, то средняя арифметическая увеличится или уменьшится на ту же величину. 4. Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно уменьшится или увеличится в А раз. 5. Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменится. Исходя из данного свойства можно заключить, что в случае равенства всех весов между собой расчеты по средней арифметической взвешенной и средней арифметической простой приведут к одному и тому е результату.
Другие виды средних При расчете статистических показателей помимо средней арифметической могут использоваться и другие виды средних.
Средняя квадратическая - Применяется для осреднения величин, выраженных в виде квадратных функций (например, средние диаметры колес, труб, стволов, средние стороны квадратов и др.). Используется при расчете показателей вариации (СКО).
Средняя кубическая - применяется, когда необходимо сохранить неизменной сумму кубов исходных величин. Находятся: строительные объемы зданий, элеваторов, бассейнов.
Средняя гармоническая взвешенная. Рассмотрим вариант, когда известен числитель исходного соотношения средней, но неизвестен его знаменатель. Средняя гармоническая может применяться для усреднения тех же признаков, но с другой формой представления данных. Может быть не только взвешенной, но и простой.
Средняя геометрическая обладает свойством сохранять неизменным произведение исходных величин. Применяется для усреднения относительных величин, а также для нахождения качественного среднего между минимальным и максимальным значением.
Средняя хронологическая – применяется на временных рядах, может быть простой и взвешенной. Структурные характеристики вариационного ряда Мода (Мо) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой.
Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Главное свойство: сумма абсолютных значений признака от медианы меньше, чем от любой другой величины
Определение моды в интервальных рядах:
xmo – начало модального интервала, h – ширина модального интервала, fmo – частота модального интервала, fmo-1,fmo+1 – частоты соседних интервалов.
Определение медианы в интервальных рядах:
xme – начало медианного интервала, Sme-1 – накопленная частота интервала, предшествующего медианному fme – частота медианного интервала
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию. Если Мо < Ме < x̅— имеет место правосторонняя асимметрия, при x̅ < Ме< Мо следует сделать вывод о левосторонней асимметрии ряда.
Аналогично с нахождением медианы в вариационных рядах распределения можно отыскать значение признака у любой по порядку единицы ранжированного ряда. Так, например, можно найти значение признака у единиц, делящих ряд на четыре равные части, на десять или сто частей. Эти величины называются «квартили», «децили»(10 частей) и «перцентили»(100 частей).
Квартили представляют собой значения признака, делящие ранжированную совокупность на четыре равновеликие части. Различают квартиль нижний (Q1), отделяющий 1/4 часть совокупности с наименьшими значениями признака, и квартиль верхний (Q 3), отсекающий 1/4 часть с наибольшими значениями признака. Это означает, что 25% единиц совокупности будут меньше по величине Q1; 25% единиц будут заключены между Q2 и Q3; 25% - между Q2 и Q3 и остальные 25% превосходят Q3. Средним квартилем Q2 является медиана.
Для расчета квартилей по интервальному вариационному ряду используются формулы:
Кроме квартилей в вариационных рядах распределения могут определяться децили - варианты, делящие ранжированный ряд на десять равных частей.
Показатели вариации
Вариацией признака называют отличие (колеблемость, многообразие, изменяемость величины) в численных значениях признаков единиц совокупности и их колебания около средней величины, что и будет характеризовать совокупность. Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным относятся размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. Относительными показателями вариации являются коэффициенты осцилляции, вариации, относительное линейное отклонение и др. Самым простым абсолютным показателем является размах вариации (R).
Для анализа вариации необходим и показатель, который отражает все колебания варьирующего признака, дающий обобщенную ее характеристику. Такая средняя называется средним линейным отклонением (L). Оно вычисляется как средняя арифметическая из абсолютных значений отклонений вариант хi и (взвешенная или простая в зависимости от исходных условий) по следующим формулам:
- простое
- взвешенное
Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):
- простая
- взвешенная
— средняя квадратов вариант;
— квадрат средней вариант.
Т.о., дисперсия есть средняя величина квадратов отклонений.
– момент второго порядка;
– момент первого порядка;
– условные варианты
Дисперсию используют не только для оценки вариации, но и для измерения связей между исследуемыми факторами; распределение дисперсии на составляющие позволяет оценить влияние разных факторов, которые обусловливают вариацию признака. Среднее квадратическое отклонение, как и дисперсия, выступает в качестве широко используемого обобщающего показателя вариации.
В условиях нормального распределения существует следующая зависимость между величиной среднего квадратического отклонения и количеством наблюдений: в пределах х±1Ϭ располагается 0,683 или 98,3% количества наблюдений; в пределах х±2Ϭ – 95,4%; в пределах х±3Ϭ – 97,7%.
Линейный коэффициент вариации (характеризует долю усредненного значения абсолютных отклонений от средней арифметической). (VL):
Коэффициент вариации (характеризует степень однородности совокупности)(Vσ):
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 858; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |



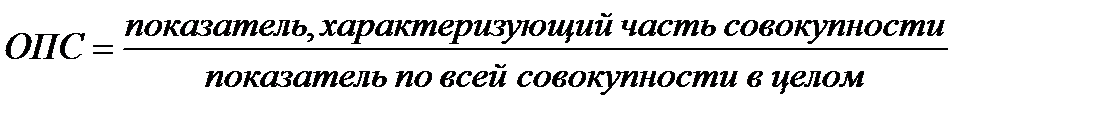


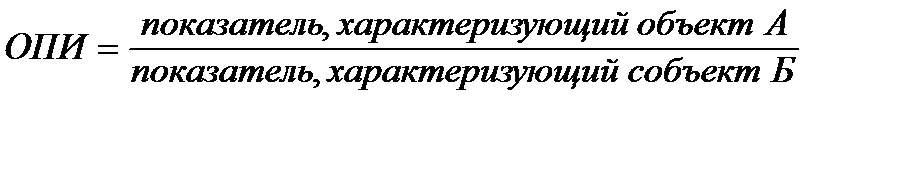
 Определить среднюю во многих случаях можно черезисходное соотношение средней (ИСС) или ее логическую формулу:
Определить среднюю во многих случаях можно черезисходное соотношение средней (ИСС) или ее логическую формулу: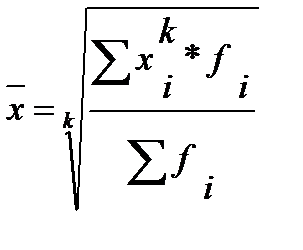
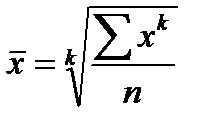

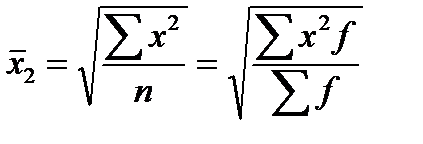
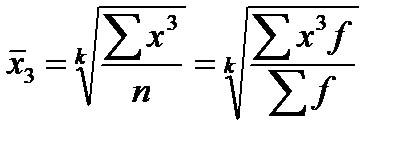
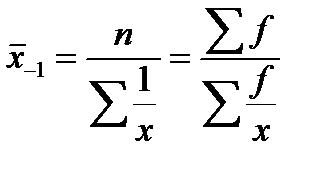
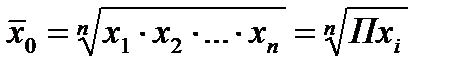
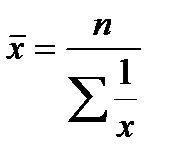

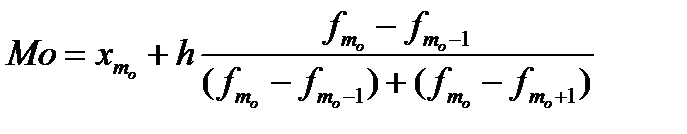
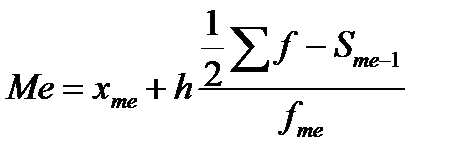


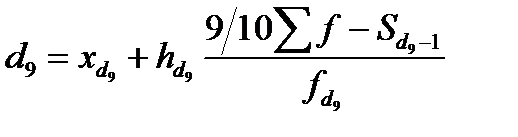

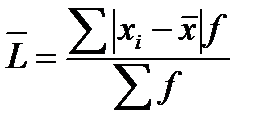
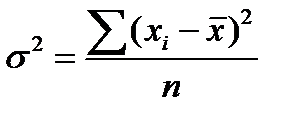

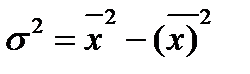 Дисперсия может быть рассчитана как разность средней квадратов вариант и квадрата средней вариант:
Дисперсия может быть рассчитана как разность средней квадратов вариант и квадрата средней вариант: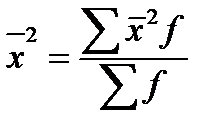
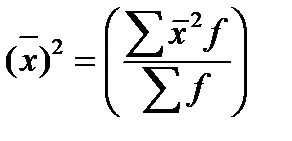
 По равноинтервальному ряду распределения или дискретному ряду с одним и тем же шагом между значениями осредняемого признака возможен расчет дисперсии способом «моментов»:
По равноинтервальному ряду распределения или дискретному ряду с одним и тем же шагом между значениями осредняемого признака возможен расчет дисперсии способом «моментов»: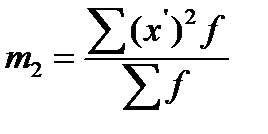
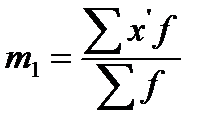
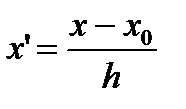
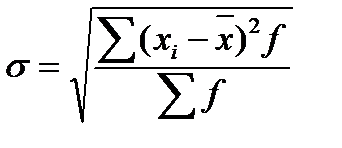
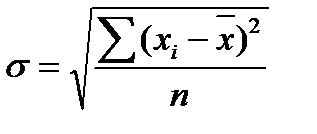
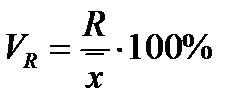 Для осуществления сравнений колеблемости различных признаков в одной и той же совокупности, а также при сопоставлении признака в нескольких совокупностях с разными средними арифметическими используются также относительные показатели вариации (по отношению к среднему значению признака):
Для осуществления сравнений колеблемости различных признаков в одной и той же совокупности, а также при сопоставлении признака в нескольких совокупностях с разными средними арифметическими используются также относительные показатели вариации (по отношению к среднему значению признака): Коэффициент осцилляции (VR) (колеблемость крайних значений признака вокруг средней):
Коэффициент осцилляции (VR) (колеблемость крайних значений признака вокруг средней):




